基于PCA算法生成平均脸
在智能算法专题设计课中,我们学习了PCA算法,并学会利用PCA算法生成平均脸,下面是步骤以及我的一些思考
了解PCA算法
PCA算法本质上是一种降维算法。
**PCA的算法思路:**数据从原来的坐标系转换到新的坐标系,由数据本身决定。转换坐标系时,以方差最大的方向作为坐标轴方向,因为数据的最大方差给出了数据的最重要的信息。第一个新坐标轴选择的是原始数据中方差最大的方向,第二个新坐标轴选择的是与第一个新坐标轴正交且方差次大的方向。重复该过程,重复次数为原始数据的特征维数。
**PCA算法的要点:**通过这种方式获得的新的坐标系,我们发现,大部分方差都包含在前面几个坐标轴中,后面的坐标轴所含的方差几乎为0。于是,我们可以忽略余下的坐标轴,只保留前面的几个含有绝大部分方差的坐标轴。事实上,这样也就相当于只保留包含绝大部分方差的维度特征,而忽略包含方差几乎为0的特征维度,也就实现了对数据特征的降维处理。
生成特征脸的步骤
输入:训练样本集 D=x(1),x(2),…,x(m)D=x(1),x(2),…,x(m) ,低维空间维数 d′d′ ;
过程:.
第一步:对所有样本进行中心化(去均值操作): x(i)j←x(i)j−1m∑mi=1x(i)jxj(i)←xj(i)−1m∑i=1mxj(i) ;
第二步:计算样本的协方差矩阵 XXTXXT ;
第三步: 对协方差矩阵 XXTXXT 做特征值分解 ;
第四步:取最大特征值对应的特征向量(这里可以通过能量进行选择)
第五步:最终得到的特征向量便是特征脸
代码逐步分析
(1)对样本进行中心化:
这里包括读入所给的32张图片,将每张图片抽拉成一列(可以用a=a(:)的办法),averageFace为自己写的定义平均脸的函数。同时需要注意将原始脸数据转换一下数据类型,否则进行中心化相减时将会因为数据类型不一致而报错。
[averFace,oriFace]=averageFace(32,'s','.bmp');
averFace=averFace(:);%转成一列
oriFace=double(oriFace);
for i=1:32
oriFace(:,i)=oriFace(:,i)-averFace;
end
计算平均脸的函数:
function [aver,originalFace] = averageFace(num,beforeName,endName)
%计算平均脸的函数
%输入:数据里的所有的脸,包括图片的张数,图片的前缀名,图片的后缀名
%输出:平均脸、原始的所有图片构成的矩阵、
%首先,构造一个矩阵,用于存放每个图片后来构成的图像
aver=ones(10000,1);
for i=1:num
face=imread(strcat(beforeName,num2str(i),endName));%读入图片数据
%每读一张,就将它转化为列向量
column=face(:);
%把转化后的列向量添加到一个矩阵中
aver=[aver column];
end
%删除矩阵的第一列:为了构造矩阵而添加的一列
aver(:,1)=[];
originalFace=aver;
%计算该矩阵每一行的平均值,形成一列平均值的向量
aver=mean(aver,2);
%将平均值的向量还原成矩阵,即为平均脸,返回平均脸
aver=reshape(aver,100,100);
end
(2)计算样本的协方差矩阵:
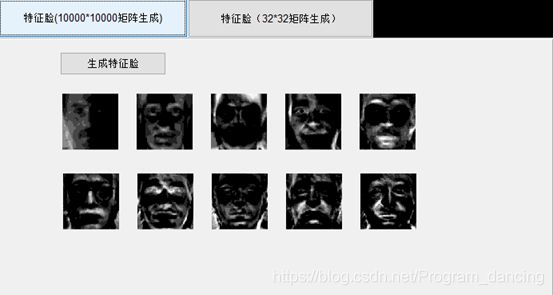
这里是(10000,32)(3210000),所以得到的协方差矩阵为10000*10000,比较大。
%第二步:计算样本的协方差矩阵
covMatrix=oriFace*oriFace';
(3)计算样本的特征值和特征向量:
在matlab中可以使用函数eig得到协方差矩阵的特殊值,由于协方差矩阵比较大,所以计算过程十分耗时,下面有谈到另一种计算特征向量和特征值的办法。
%第三步:对协方差矩阵作特征值分解
%获得协方差矩阵的特征值的对角矩阵D
[V,D]=eig(covMatrix);
%取对角矩阵的特征值
featureValue=diag(D);
(4)根据能量找到最大的几个特征值,并找到最大特征值对应的特征向量。
%对特征值进行从大到小的排序
bigToSmall=sort(featureValue,'descend');
%第四步:取最大的d个特征值所对应的特征向量
%这里通过能量确定d的取值
d=0;%d的初始取值为0
someEnergy=0;%前项的能量
allEnergy=sum(bigToSmall(:));%所有的特征能量
while(someEnergy/allEnergy<0.9)
d=d+1;
someEnergy=sum(bigToSmall(1:d,:));
end
%寻找特征值对应的特征向量
featureVector=zeros(10000,1);
for i=1:d
nowNumber=bigToSmall(i);%从大到小找到此时的值
[row,column]=find(D==nowNumber);%在原来的特征值数组中定位
findVector=V(:,column);%根据原来的特征值数组位置找到其对应的特征向量
featureVector=[featureVector findVector];
end
featureVector=featureVector(:,2:d+1);%删掉之前添加的数据
(5)最终找到的特征向量即为特征脸,只需要使用reshape函数转成原始图片大小即可。
matlab整体实现代码
function [] = PCACalculator()
%PCA算法计算出特征脸
%输入:训练样本集,低维空间维度:d
%输出:特征脸
%第一步:对所有样本进行中心化
%得到平均脸函数中,获得的原始所有脸矩阵+平均脸矩阵
[averFace,oriFace]=averageFace(32,'s','.bmp');
averFace=averFace(:);%转成一列
oriFace=double(oriFace);
for i=1:32
oriFace(:,i)=oriFace(:,i)-averFace;
end
%第二步:计算样本的协方差矩阵
covMatrix=oriFace*oriFace';
%第三步:对协方差矩阵作特征值分解
%获得协方差矩阵的特征值的对角矩阵D
[V,D]=eig(covMatrix);
%取对角矩阵的特征值
featureValue=diag(D);
%对特征值进行从大到小的排序
bigToSmall=sort(featureValue,'descend');
%第四步:取最大的d个特征值所对应的特征向量
%这里通过能量确定d的取值
d=0;%d的初始取值为0
someEnergy=0;%前项的能量
allEnergy=sum(bigToSmall(:));%所有的特征能量
while(someEnergy/allEnergy<0.9)
d=d+1;
someEnergy=sum(bigToSmall(1:d,:));
end
%寻找特征值对应的特征向量
featureVector=zeros(10000,1);
for i=1:d
nowNumber=bigToSmall(i);%从大到小找到此时的值
[row,column]=find(D==nowNumber);%在原来的特征值数组中定位
findVector=V(:,column);%根据原来的特征值数组位置找到其对应的特征向量
featureVector=[featureVector findVector];
end
featureVector=featureVector(:,2:d+1);%删掉之前添加的数据
%第五步:将原样本矩阵与投影矩阵相乘即为降维后的数据集
%specialFace=oriFace*featureVector;
%将会生成多张特征脸,这里要将矩阵的每一列重新合成一张照片
%由于生成时间慢,这里可以把图片保存下来
for i=1:d
name=strcat('featureFace',num2str(i),'.bmp');
pic=featureVector(:,i);
picToOri=reshape(pic,100,100);
imwrite(picToOri,name);%保存图片
end
end
关于PCA算法中求特征向量的思考
找寻简单的求特征向量的方法:
在PCA算法的过程中,其中有一个步骤是生成样本的协方差矩阵,如果采用原始方法直接生成它的协方差矩阵的话,那么计算量将非常大,我在这里测试了一下,改改需要十多分钟到二十分钟左右。而能否有简单的办法呢?
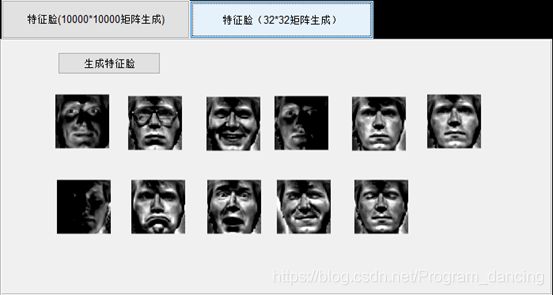
在这里涉及到数学上的转化:可以通过其他办法得到原始协方差矩阵生成的特征向量。原始样本协方差矩阵为C=AA’(此实验中将生成1000010000的矩阵),而用C=A’A(此实验中将生成3232的矩阵)也可以得到对应的特征向量,为A*ei,而整个过程得到的矩阵大小大大减小,计算量也是大大减小。证明如下:

其中,ei是C’=ΦTΦ的第i个特征向量,vi是C=ΦΦT的第i个特征向量,由证明可以看到,vi=Φei。所以通过求解C’=ΦTΦ的特征值分解得到ei,再左乘Φ就得到C=ΦΦT的特征向量vi了。也就是我们想要的特征脸。
function [] = annotherPCA()
[averFace,oriFace]=averageFace(32,'s','.bmp');
averFace=averFace(:);%转成一列
oriFace=double(oriFace);
for i=1:32
oriFace(:,i)=oriFace(:,i)-averFace;
end
%第二步:计算样本的协方差矩阵
covMatrix=oriFace'*oriFace;
%第三步:对协方差矩阵作特征值分解
%获得协方差矩阵的特征值的对角矩阵D
[V,D]=eig(covMatrix);
%取对角矩阵的特征值
featureValue=diag(D);
%对特征值进行从大到小的排序
bigToSmall=sort(featureValue,'descend');
%第四步:取最大的d个特征值所对应的特征向量
%这里通过能量确定d的取值
d=0;%d的初始取值为0
someEnergy=0;%前项的能量
allEnergy=sum(bigToSmall(:));%所有的特征能量
while(someEnergy/allEnergy<0.9)
d=d+1;
someEnergy=sum(bigToSmall(1:d,:));
end
%寻找特征值对应的特征向量
featureVector=zeros(10000,1);
for i=1:d
nowNumber=bigToSmall(i);%从大到小找到此时的值
featureVector=[featureVector oriFace*nowNumber];
end
featureVector=featureVector(:,2:d+1);%删掉之前添加的数据
%第五步:将原样本矩阵与投影矩阵相乘即为降维后的数据集
%specialFace=oriFace*featureVector;
%将会生成多张特征脸,这里要将矩阵的每一列重新合成一张照片
for i=1:d
name=strcat('32featureFace',num2str(i),'.bmp');
pic=featureVector(:,i);
picToOri=reshape(pic,100,100);
imwrite(picToOri,name);%保存图片
end
问题:
使用两种方法生成的特征脸却不一样?不由地思考到:原本是1000010000的矩阵,应该能够得到10000个特征值和特征向量,但是使用简化的办法的话,生成3232的矩阵,只能得到32个特征值和特征向量,那么能否保证最大特征值保留下来了?在10000个特征值中得到的对应的最大的几个特征向量被保留在了32个特征值对应的特征向量中了嘛?根据生成的特征脸不同,
可以初步断定是没有的。所以我觉得这种办法只能够生成特征脸,但是这个特征脸并不是最大的几个特征值对应的特征向量所生成的,所以这应该得不到最优解。