智力拼图问题–关于回溯和并行：单线到多线程再到GPU编程的进阶（一）

转自个人博客：http://siukwan.sinaapp.com/?p=671
相关文章：
智力拼图问题–关于回溯和并行：单线到多线程再到GPU编程的进阶（一）
智力拼图问题–关于回溯和并行：单线到多线程再到GPU编程的进阶（二）
智力拼图问题–关于回溯和并行：单线到多线程再到GPU编程的进阶（三）

最近算法设计上面有一个回溯的题目，要求使用回溯算法解答，题目如下：

智力拼图问题

设有12个平面图形（1,2,3,4,5,6,7,8,9，a,b,c）如下图所示。每个图形的形状互不相同，但它们都是由5个大小相同的正方形组成。如下图中这12个图形拼接成一个6*10的矩阵。设计一个算法，计算出用这12个图形拼接成给定矩形的拼接方案。

题目限制并没有很明确，但是通过网上搜索，可以知道有如下要求：

（1）12个图形就是上图所展示的图形；

（2）这些图形可以进行旋转（每次旋转90°）或者翻转；

（3）每个图形使用1次。

（4）矩阵的形状不一定为6*10，但是面积一定为60，即可以出现3*20，4*15，5*12等等的情况。

一、分析：

先对题目进行简单的分析，由浅到深：

（1）题目需要求出拼接方案，我们默认求出所有的拼接方案，那么没有办法使用动态规划或者贪心算法进行求解，只能够使用深度搜索，进行适当的剪枝。

（2）我们先考虑没有旋转和翻转的情况，那么这12个图形的排列组合情况一共有12!这么多，即479001600种。我们假设每秒遍历1000种组合情况，那么求解需要最多47900.16秒，换算一下，大概约13个小时。假如每秒遍历10万种情况，那么只需要7.98336分钟，约8分钟。实际上深度搜索的过程中，可以进行剪枝，所以运行时间远小于这个值。下面是6*10的矩阵，在图形没有旋转和翻转的情况下，所花费的时间：

只有1秒，因为没有旋转，很容易就剪枝了。

（3）经历了上面的推算，我们尝试加入旋转和翻转，假设每个图像都可以进行旋转和翻转，那么每个图形都可以演化为8种情况，旋转0°+不反转，旋转0°+反转，旋转90°+不反转，旋转90°+反转。。。。。那么总的排列组合情况有12!*8^12，12!（479001600）在2^28（268435456）和2^29（536870912）之间，而8^12相当于2^36，把12!当作2^28，那么总的排列组合数量为2^28*2^36=2^64。

2^64是不是一个很熟悉的数字？没错，就是汉诺塔传说中的64个金片，每秒移动一个金片总共需要5845亿年，好吧，我们的计算机处理速度会更快，那么每秒遍历1000万种情况，那么仍需5.845万年！

当然，实际上会剪枝的，这个只是给大家一个概念。

二、如何剪枝：

（1）从排列组合来看，12!*8^12种，实际上，有些图形旋转或者翻转后是重复的。例如题目图中的8号图形，无论怎么旋转或者翻转，都是一样的，那么遍历的时候，不用再去遍历它旋转或者翻转的情况。同样，1号和a号图形等等，在旋转或者翻转的时候都存在重复的情况，我们可以把这些重复的情况去掉，这样8^12就可降下来了。

（2）第二个剪枝的情形属于正常的遍历排除，我们一个一个图案填充上去，即时检测是否能够填充，能够填充的就继续进行DFS，不能填充的就遍历下一个图形。

（3）会有帮助但是效果不是很明显的剪枝，在实际的填充过程中，我们发现，矩阵填充出出现一些孤立的连通区域，面积为1、2、3等等。实际上，我们每个图形的面积为5，那么假如矩阵出现面积小于5的连通区域，那这个方案也不用再继续DFS了。实际上，要检测连通区域，就会涉及到并查集，而并查集通过递归（也可以改成循环）进行集合的检测和划分，但是对于每种遍历的情况都使用并查集去划分搜索连通区域，会大大地增加时间复杂度。

简化的版本就是，搜索出矩阵的第一个未被填充的空格坐标，检测这个坐标的上下左右（实际上只检测下右即可）是否已经被填充，如果被填充就return，没有被填充就继续DFS。这个版本实际上是检测单个的面积为1的连通区域，对剪枝是有帮助的（实际上帮助比较少），而且只是多加两个判断，对时间复杂度影响不大。

（4）除了上述的剪枝，我们还尝试另外一种填充方法。我们默认的填充方法，称之为顺序填充，是从左到右从上到下依次填充，这样做的缺点就是下方空余的连通区域较大，不利用使用（3）的方法进行剪枝。如何更好地利用（3）方法进行剪枝呢？我们提出了一种回旋填充的方法，一次填充4个角，这样可以从外围往中间逼近，从而更容易产生比顺序填充更小的连通区域。这些更小的连通区域就更有可能适合方法（3）的剪枝。

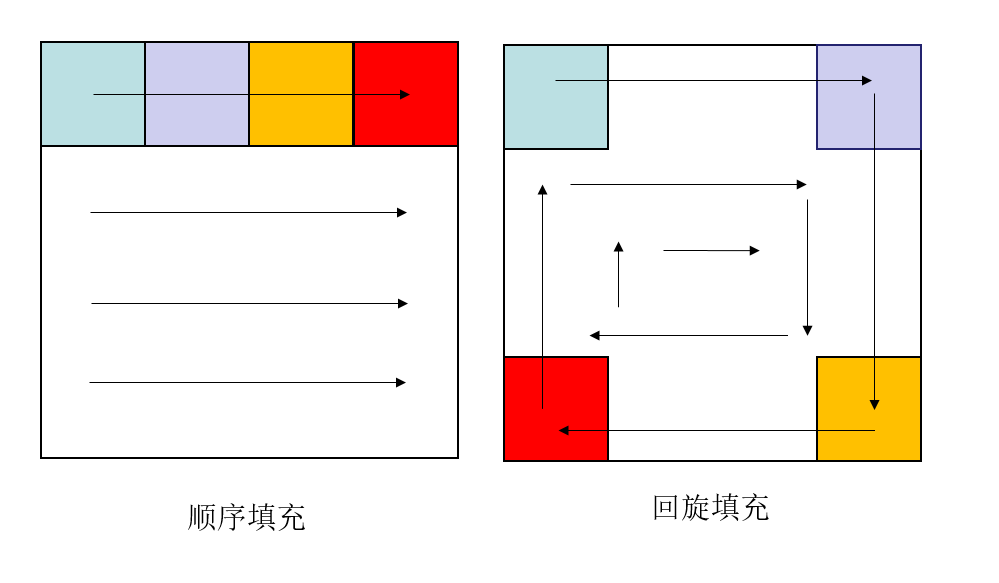
但是，通过实践证明，回旋填充会导致更加糟糕的时间复杂度。我们进行了对比实验，对6*10的矩阵进行填充。我们填充6*10的矩阵，使用单线程的DFS，总共需要耗时38分钟，答案个数为9356个，总共遍历了4358万种情况（省去了万位以下的数字）。而使用回旋填充的方法，我们填充6*10的矩阵，遍历71分钟后（程序并未结束），只搜索到了99个答案，遍历了5800万种情况。那么保守估计，等到遍历出9356个答案，大约需要再花费71*10分钟（假设每71分钟遍历出99个答案），遍历的情况总数将会远超4358万种。

仔细分析，每个图形只占用了5个面积，而矩阵的面积为60！进行回旋填充，我们期望出现面积为1的连通域，需要填充多次。而相比之下，回旋填充相当于选择了更为广阔的空间进行图形的填充，而顺序填充由于宽度的限制（例如宽度为3，4，5，6），很容易就对图形判断是否合适。而回旋填充每次选择了空间余量较大的角落进行填充，因此会遍历更多的次数！

综上所述，我们只能够利用方法（1）（2）（3）进行剪枝深度搜索，也就是使用回溯法。具体实现：

下一篇文章，我们会介绍如何进行算法设计：
智力拼图问题–关于回溯和并行：单线到多线程再到GPU编程的进阶（二）