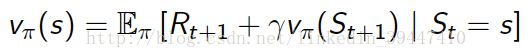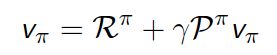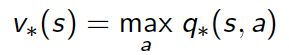七月算法强化学习 第一课 学习笔记

一、强化学习简介与应用：

1.强化学习定义：
强化学习是机器学习中的一个领域，强调如何基于环境而行动，以取得最大化的预期利益。其灵感来源于心理学中的行为主义理论，即有机体如何在环境给予的奖励或惩罚的刺激下，逐步形成对刺激的预期，产生能获得最大利益的习惯性行为。

2.强化学习起源：

Artificial Intelligence
Control Theory
Operation Research
Cognitive Science & Psychology

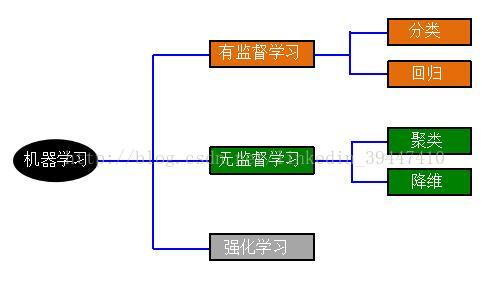
有监督学习：Labeled数据，直接反馈，预测未知label数据
无监督学习：Unlabeled数据，无反馈，寻找数据隐藏结构
强化学习特点：1）无监督数据，只有奖励信号 2）奖励信号不一定实时，大部分情况奖励信号滞后 3）研究的非i.i.d数据，时间序列 4）当前的行为影响后续数据分布

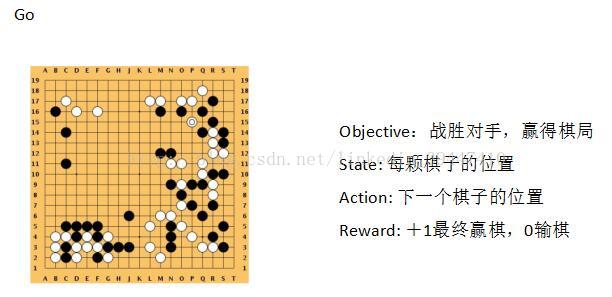
举例：Alpha Go、Atari游戏 、机器人控制、自动驾驶直升机 (http://heli.stanford.edu/)、自动驾驶、自动交易 、etc..

二、强化学习数学模型

如何建立强化学习数学模型：
Model of uncertainty
Environment, actions, Agent knowledge
Focus on decision making
Maximize long-term reward

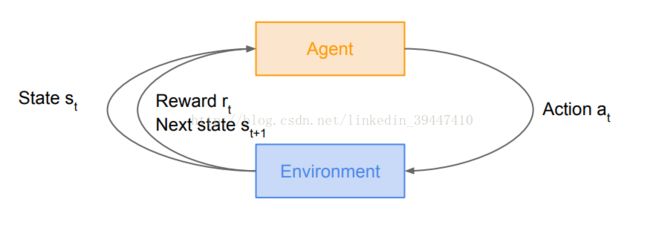
Reward奖励 Rt 标量函数 奖励假设：所有问题解决的目标都可以被描述成最大化累积奖励
History历史 Ht 历史是观测、行为、奖励的序列：Ht = O1, R1, a1,..., Ot-1, Rt-1, at-1, Ot, Rt, at 

State状态 St 状态是所有决定将来的已有的信息，是关于历史的函数 St ＝f (Ht)

Action动作 at

Sequential Decision Making序列决策：1）目标：选择一定的行为系列以最大化未来的总体奖励 2）这些行为可能是一个长期的序列 3）奖励可能而且通常是延迟的 4）有时候宁愿牺牲即时（短期）的奖励以获取更多的长期奖励

Markov Property:
A state St is Markov iff :   P(St+1 | St, St-1,...,S1) = P(St+1 | St) 
The state captures all relevant information from the history.
Once the state is known, the history may be thrown away.
Transition Matrix:  Pss’  = P(St+1  =s’ | St = s)  (finite state).

How to choose state to obtain a Markov Process?

Example: Helicopter (位置，速度，角速度)

State 选择不正确：memory effect !!!

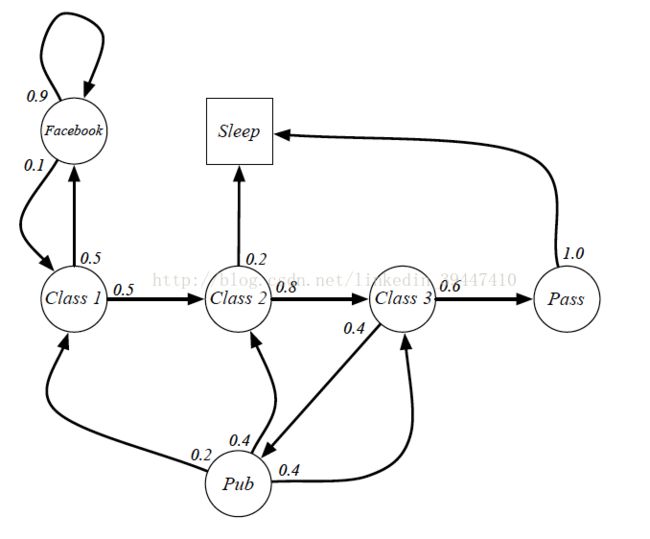
Markov Process马尔科夫过程:
随机过程S1, S2,…满足马尔科夫性 

Sample Trajectories:

Markov Decision Process (MDP)马尔科夫决策过程:

MDP是绝大多数的RL问题的数学表示
马尔科夫性
环境：Pass’  &  Ras

－ t=0, 初始状态s0 ~ P(s0)
－ while Not done:
－ AI根据st选择action at
－ 环境给出reward rt ~ R(.|st, at)
－ 环境给出下一时刻状态st+1 ~ P(.|st, at)
－ AI 接收rt和st+1

－ t=0, 初始状态s0 ~ P(s0)
－ while Not done:
－ AI根据st选择action at
－ 环境给出reward rt ~ R(.|st, at)
－ 环境给出下一时刻状态st+1 ~ P(.|st, at)
－ AI 接收rt和st+1

Policy策略π 
Deterministic Policy  π :  S --> A 
Stochastic Policy  π(a | s) = P[At = a | St = s]
累计回报Gt:(why discount?)

RL Objective: 找出最优策略π*使得累计回报最大

State-Value Function价值函数
评价基于策略π下状态的好坏（长期价值）
表示从状态s开始，遵循策略π能得到的收获的期望值

State-action Value Function 动作价值函数
评价基于策略π，在状态s下执行动作a的好坏
表示在状态s下先执行动作a，然后遵循策略π能得到的收获的期望值

三、强化学习算法综述

MDP Problems
MDP Planning: 已知模型，找到最优策略
MDP Learning: 未知模型，理解环境，尝试找到最优策略

RL Algorithms
Value Based
Policy Based
Actor-Critic

RL Algorithms
State and Action space is discrete and small
State and Action space is large: function approximation, Deep RL

四、MDP Planning

给定模型
策略评估: 给定策略π，计算累计回报期望值 （求解Bellman Expectation Eq.  ）

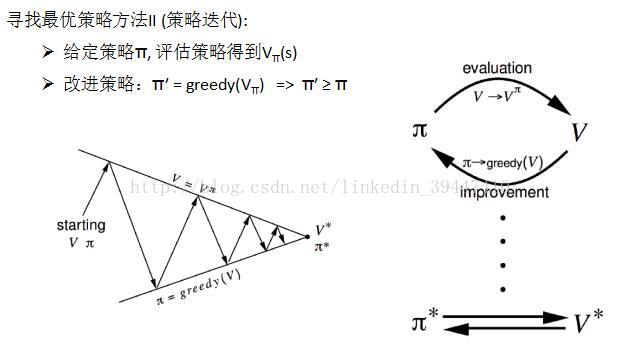
寻找最优策略:
极大化从任何状态开始的累计回报期望值

MDP Planning 总结：

Problem	Equation	Algorithm
策略评估	Bellman Expectation Eq.	Iterative Policy Evaluation
寻找最优策略	Bellman Expectation Eq. + Greedy Policy Improvement	Policy Iteration
寻找最优策略	Bellman Optimality Eq.	Value Iterat

Value Iteration
For each iteration, O(|A||S|2)
Iteration numbers, Poly(|A|, |S|, 1/(1-γ))
Policy Iteration
For each iteration, O(|S|3 + |A||S|2)
|S|3 for policy evaluation, |A||S|2 for improvement
Iteration numbers: unknown, but faster in practice.