Unity Shader:Waveform波形(3)-复合波
2D复合波
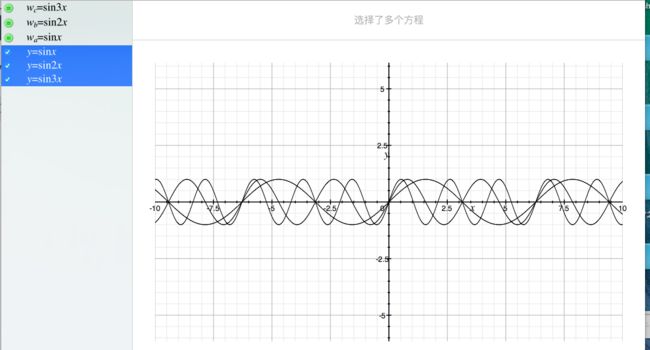
(图1:在xy平面有三个波,y1=sinx,y2=sin2x,y3=sin3x)
根据叠加原理(superposition principle),可以将这三个波组合成一个复合波形,这个复合波既是三个波形相加后的结果:
y=sinx+sin2x+sin3x。
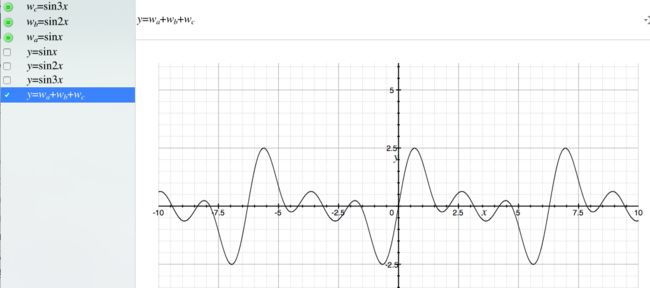
(图2:相加后生成的复合波)
3D复合波
利用方向向量改变3D空间中一个平面的波形的方向
设任意一点点p,方向向量a=float2(1,0).
p.xy=dot(float2(1,0),p.xy)
再求它的正弦函数:
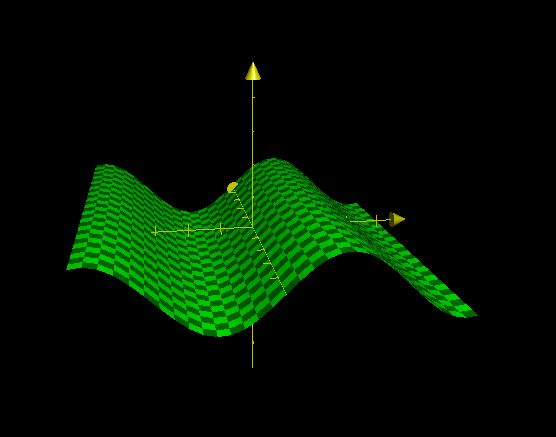
(图3,左手坐标系。z=sin(dot(float2(1,0),p.xy))
如果改变方向向量a为0,1。p.xy=dot(float2(0,1),p.xy)
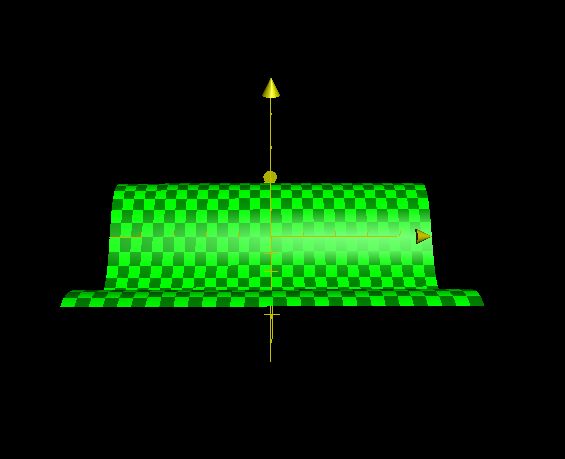
(图4,左手坐标系。z=sin(dot(float2(0,1),p.xy))
如果改变方向向量a为(1,1)。p.xy=dot(float2(1,1),p.xy)
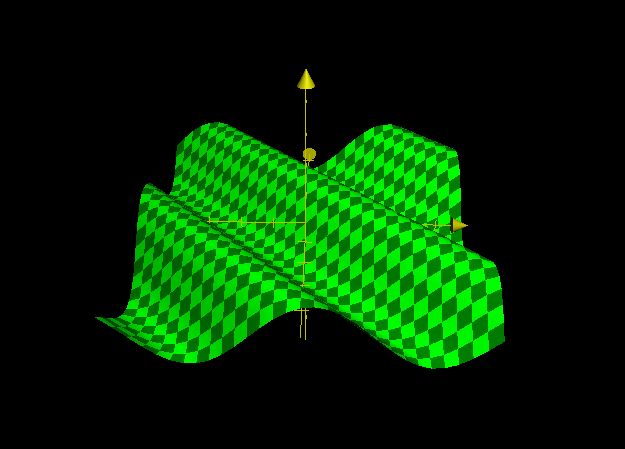
(图5,左手坐标系。z=sin(dot(float2(1,1),p.xy))
以上表明3D空间中的某个平面的每个点在该平面的2D坐标与一个方向向量进行点乘,那么通过这些点乘后的点与第三个维度的坐标所计算出的波形的方向与此向量的方向一致。在此可以将点乘理解为把方向向量的方向与强度赋予给一个点的集合。
3D空间中波的合成
在3D空间中,叠加原理依然适用:
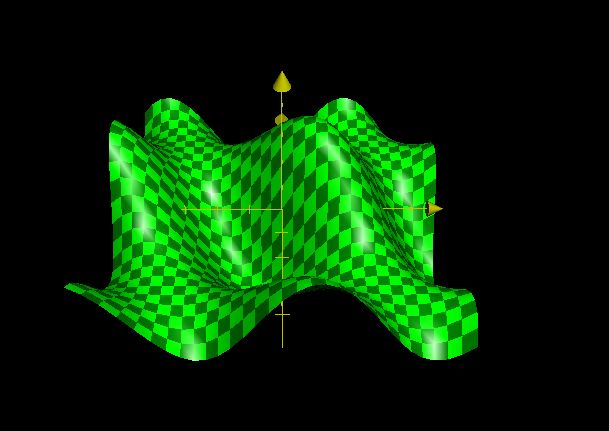
(图6,左手坐标系,z=sin(y)+sin(x)+sin(x+y))
将复合波应用到复杂系统中
测试上文的复合波形
以下是在Unity中用Shader通过正弦函数的变种在片段着色器中重新计算像素位置与法线,并进行正向光照计算后的效果。

(图7:一个xy点乘(1,0)的正弦函数波形)

(图8:一个xy点乘(1,0)与一个xy点乘(0,1)的复合正弦函数波形)

(图8:xy点乘(1,0),(0,1),(1,1)后的三个波形组成的复合波形)
圆形波
通过上文的方向波可知,利用一个方向向量可以将改变波形的方向,那么圆形波的特点是任意一点的波形方向都是波形中心点射向该点的方向。利用Shader的并发编程特性,可以很方便的用当前像素坐标减去波形中心点坐标即可得出需要的方向向量。
dir=normalize(i.worldPos-waveCenterPos);

(图9:一个圆形波)

(图10:不同频率与位置的两个圆形波合成)

(图11:不同频率与位置的四个圆形波合成)

(图12:不同频率与位置的四个圆形波合成,根据波纹与波中心的距离对波的力度进行了衰减,可更清楚看到波中心点)
通过以上可得知,利用波形可叠加的特性,只要有正确的方向向量,任何复杂波形都是可以模拟。
海浪与水纹
在Unity Standard Assets中的Water4水模拟项目中的Shader中有一段计算Gerstner wave的代码,里面有利用到复合波:
half3 GerstnerOffset4_Official (half2 xzVtx, half4 steepness, half4 amp, half4 freq, half4 speed, half4 dirAB, half4 dirCD)
{
half3 offsets;
half4 AB = steepness.xxyy * amp.xxyy * dirAB.xyzw;
half4 CD = steepness.zzww * amp.zzww * dirCD.xyzw;
half4 dotABCD = freq.xyzw * half4(dot(dirAB.xy, xzVtx), dot(dirAB.zw, xzVtx), dot(dirCD.xy, xzVtx), dot(dirCD.zw, xzVtx));
half4 TIME = _Time.yyyy * speed;
half4 COS = cos (dotABCD + TIME);
half4 SIN = sin (dotABCD + TIME);
offsets.x =dot(COS, half4(AB.xz, CD.xz));
offsets.z =dot(COS, half4(AB.yw, CD.yw));
offsets.y = dot(SIN, amp);
return offsets;
}
以上的方法中利用了向量化计算,看起来不是很直观。dirAB.xy,dirAB.zw,dirCD,xy,dirCD.zw分别是四个波的方向向量。xzVtx保存的是世界空间的x,z坐标点。这样将世界空间中xz平面的每个点与4个方向向量进行点乘,再用sin计算出第三维度的y的波形高度值保存到SIN,offsets.y再次利用dot对4个波的高度偏移值进行相加,既完成了四个波的叠加。其中的amp,freq,speed等变量都是用来控制波形的形状(可见前篇文章)。
除了计算高度y值,上面的方法还根据Gerstner Wave公式对xz坐标也做了位移计算,形成了更加复杂的波形。此波形,既Gerstner波的特点既是波峰处更加尖锐,xz坐标逐渐向波峰靠拢,与真实海洋波浪更加相近。
Gerstner Wave原始公式:(Jerry Tessendorf 2004)
x = x0 − (k/k)A sin(k · x0 − ωt)
y = A cos(k · x0 − ωt)
(更原始的公式尚未找到,尚未搞懂公式思路)
NVIDIA在GPU gems1 第一章中(equation 9)有将以上公式展开成可以在3D空间中计算的函数,与Unity Water4的算法基本一致。(尚未搞懂其函数从原始函数转换出来的方法与思路)
(图13:根据Gerstner Wave对一个简单平面网格进行顶点位移)

(图14:Unity Water4的海洋渲染效果,海浪的效果既是依赖于Gerstner Wave的计算)
复合波与折射
将对圆形波的计算应用于法线的偏移,偏移后的法线用于折射采样,再结合复合波的叠加,多个采样后的颜色叠加同样也可以呈现波形效果同时又呈现了一个空间扭曲的特效效果。
(图15:正常渲染的场景)
(图16:用一个圆形波的法线进行折射采样)
(图17:用一个圆形波的法线进行折射采样)
(图18:用两个圆形波的法线进行折射采样与叠加)
(图19:用两个圆形波的法线进行折射采样与叠加,可看出平面顶点没有变化,也没有单独对平面进行光照渲染,但是折射采样叠加后的扭曲的场景所呈现出的波形形状更加细节与立体)
————————————————————————————
参考:
Shader FX/Water4 — UNITY
GPU gems1 —Nvidia
-https://developer.nvidia.com/gpugems/GPUGems/gpugems_app01.html
Simulating Ocean Water —Jerry Tessendorf
-http://www-evasion.imag.fr/Membres/Fabrice.Neyret/NaturalScenes/fluids/water/waves/fluids-nuages/waves/Jonathan/articlesCG/simulating-ocean-water-01.pdf
维护日志:
2017-11-19:更改一处笔误
2020-8-15:review