图像处理100问python实现part5

0.原始图像

47-53.图像形态学操作

一系列操作基于形状来操作图像，形态学操作通过在图像上应用结构元素来产生输出图像。改变物体的形状，比如腐蚀就是“变瘦”，膨胀就是“变胖”。包括膨胀与腐蚀在内，一系列的这两者各种叠加作用的操作都称为图像的形态学操作。
最基础的形态学操作就是腐蚀和膨胀。它包含广泛的应用：
1.移除噪声
2.孤立一些单独的元素和聚合一些分散的元素
3.找到图像中的局部块状或者孔

47.膨胀

使用卷积核B对图片A进行卷积运算，求局部最大值，这个卷积核可以有任意的形状和大小，通常是一个方形或者圆形。卷积核B通常有个锚点，通常位于卷积核的中央位置。
随着卷积核扫描这个图像，我们计算叠加区域的最大像素值，并将锚点的位置用最大值替换。也就是最大化操作导致图片中亮的区域增长（所以这里面叫做膨胀）。
在实际的形态学处理中，将图像二值化后，可将待操作的像素的4-近邻与卷积核B相乘，若结果大于等于255，则将该像素设为255。卷积核B形式如下：


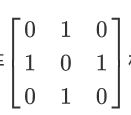
二值化后的图像：

膨胀：

48.腐蚀

腐蚀是求局部最小值的操作。腐蚀与膨胀类似，计算卷积核里面的最小元素。
随着卷积核B扫描图片，它会计算B叠加区域的最小像素值，并使用这个像素值替换锚点的值。与膨胀相似，对原始的图像应用腐蚀操作。可以看到背景亮的区域变小，而黑的区域变得很大。

腐蚀：

注意：腐蚀与膨胀都是针对白色连通域而言的，而非黑色连通域

49.开运算

开运算的具体实现：通过先进行N次腐蚀操作，再进行N次膨胀操作得到。在移除小的对象时候很有用(假设物品是亮色，前景色是黑色)，被用来去除噪声。
以下图二值图像为例：
左侧是原始图像，右侧是应用开运算之后的图像。我们可以看到左侧图像小的黑色空间被填充消失，所以开运算可以进行白色的孔洞填补。因为可以想象，我们先将黑色区域变大，然后填充部分白色区域，白色小区域这时就会被抹去，然后膨胀再将黑色区域变回，但是抹去的部分会消失，则会达到下面的效果

开运算后（time=1)

50 闭运算

闭运算先进行膨胀然后进行腐蚀操作。通常是被用来填充前景物体中的小洞，或者抹去前景物体上的小黑点。因为可以想象，其就是先将白色部分变大，把小的黑色部分挤掉，然后再将一些大的黑色的部分还原回来，整体得到的效果就是：抹去前景物体上的小黑点了。

canny边缘检测后：

闭运算后（time=1)：能够将中断的白色像素连接起来（填充黑洞）

开闭运算总结：
开运算可以去除二值化图像中残存的小块白色连通域，闭运算可以填充黑洞，使小块白色连通域轮廓增强同时连接离散的小块白色连通域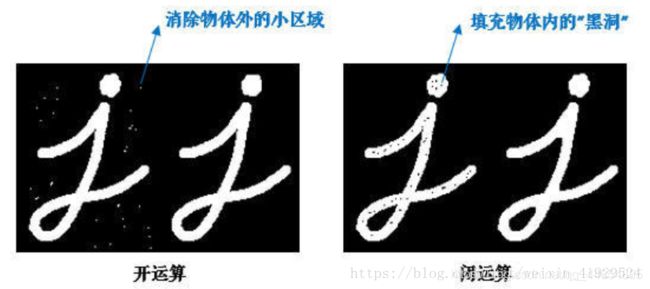

51.形态学梯度

梯度用于刻画目标边界或边缘位于图像灰度级剧烈变化的区域，形态学梯度根据膨胀或者腐蚀与原图作差组合来实现增强结构元素领域中像素的强度，突出高亮区域的外围。结果看上去就像前景物体的轮廓
特点：
1.形态学梯度操作的输出图像像素值是在对应结构元素而非局部过渡区域所定义的领域中灰度级强度变化的最大值。
2.对二值图像进行形态学操作可以将团块（blob）的边缘突出出来，可以用形态学梯度来保留物体的边缘轮廓

52.顶帽

顶帽运算是原图像与开运算的结果图的差。
在这里，我们求大津二值化之后的图像和开处理（ N=3 ）之后的图像的差，可以提取出细线状的部分或 者噪声。
顶帽运算往往用来分离比邻近点亮一些的斑块。当一幅图像具有大幅的背景的时候，而微小物品比较有规律的情况下，可以使用顶帽运算进行背景提取

53.黑帽

黑帽运算是原图像与闭运算的结果图的差。
在这里，我们求大津二值化之后的图像和闭处理（ N=3 ）之后的图像的差，在这里和顶帽运算一样，可 以提取出细线状的部分或者噪声
黑帽运算之后的效果图突出了与原图像轮廓周围的区域更暗的区域，且这一操作和选择的核大小相关。所以黑帽运算用来分离比邻近点暗一些的斑块。

代码：

##先进行大津二值化得到二值图像
def BGR2GRAY(img):
	b = img[:, :, 0].copy()
	g = img[:, :, 1].copy()
	r = img[:, :, 2].copy()

	# Gray scale
	out = 0.2126 * r + 0.7152 * g + 0.0722 * b
	out = out.astype(np.uint8)

	return out

# Otsu Binalization
def otsu_binarization(img):
	H, W = img.shape
	out = img.copy()

	max_sigma = 0
	max_t = 0

	# determine threshold
	for _t in range(1, 255):
		v0 = out[np.where(out < _t)]
		m0 = np.mean(v0) if len(v0) > 0 else 0.
		w0 = len(v0) / (H * W)
		v1 = out[np.where(out >= _t)]
		m1 = np.mean(v1) if len(v1) > 0 else 0.
		w1 = len(v1) / (H * W)
		sigma = w0 * w1 * ((m0 - m1) ** 2)
		if sigma > max_sigma:
			max_sigma = sigma
			max_t = _t

	# Binarization
	print("threshold >>", max_t)
	th = max_t
	out[out < th] = 0
	out[out >= th] = 255

	return out
	
##膨胀  time代表time次膨胀或腐蚀
def dilate(img,dil_time):
    H,W=img.shape
    #卷积核B
    B=([0,1,0],[1,0,1],[0,1,0])

    #图像边缘填充
    result=np.zeros((H+2,W+2),astype(np.uint8))
    result[H+1,W+1]=img
    mid=result.copy()
    #另一种填充方法  np.pad(result, （(1, 1)，（1，1）, 'edge') #行前后各填充一行，列前后各填充一行
for i in range(time):
    for h in range(1:H+1)：
        for w in range(1:W+1):
            near_max=np.max(B*mid(h-1:h+2,w-1:w+2))
            if near_max==255: #若4近邻像素有一个为255，就将当前像素值为255
                result[h,w]==255

    result=result[1:H+1,1:W+1].astype(np.uint8)
    return result

#腐蚀
def erode(img，ero_time):
    H, W = img.shape
    # 卷积核B
    B = ([0, 1, 0], [1, 0, 1], [0, 1, 0])

    # 图像边缘填充
    result = np.zeros((H + 2, W + 2), astype(np.uint8))
    result(H + 1, W + 1) = img
    mid = result.copy()
for i in range(time):
    for h in range(1: H + 1)：
        for w in range(1: W + 1):
            near_sum = np.sum(B * mid[h - 1:h + 2, w - 1: w + 2])
            if near_sum <255*4:  #若4近邻像素有一个不为255，就将当前像素值为0
                result[h, w] == 0

    result = result[1:H + 1, 1:W + 1].astype(np.uint8)
    return result
  #开运算
def open_operation(img,time):
    result = ilate(img, dil_time=time)
    result= erode(result, ero_time=time)
    return result


###若先进行边缘检测，如canny边缘检测，再进行闭运算，可看到闭运算能够将中断的白色像素连接起来
def close_operation(img, time):
	result = erode(img, Dil_time=time)
	result = dilate(result, Erode_time=time)
	return out
#形态学梯度
result=result_dilate - result_erode
#顶帽
result = image - result_open
#黑帽
result = image-result_close