【Caffe源码学习】im2col和col2im

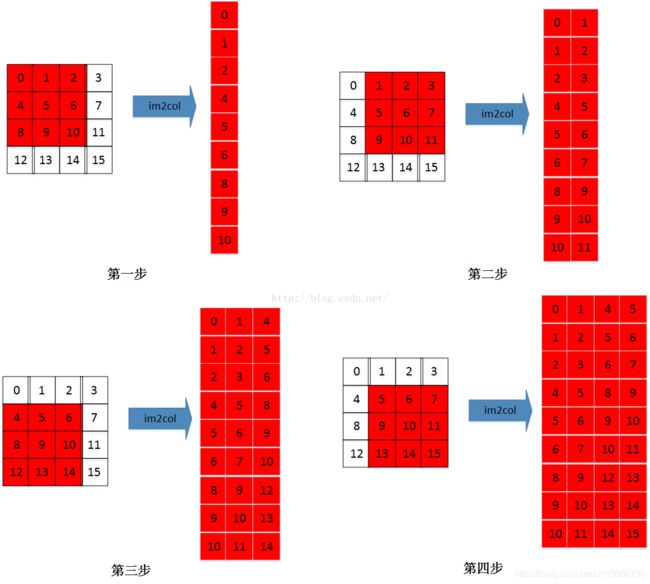
首先回顾一下卷积的实现理论细节，卷积核是一个小窗口(记录权重)，在输入图像上按步长滑动，每次滑动操作输入图像上的对应小窗区域，将卷积核中的各个权值与输入图像上对应小窗口中的各个值相乘，然后相加，并加上偏置得到输出特征图上的一个值，见下图(图片来自网络)

这里原文https://blog.csdn.net/jiongnima/article/details/69736844，巴拉巴拉有很多解释，其实我看的有点头晕，直接上图，解释逻辑和代码即可。

在这里先声明一点，caffe中的im2col是按一个卷积小窗内的数据拍成一列的排列方式（一行的排列方式matlab用到了，但caffe就是一列的方式），记住这种排列方式以便于你能相对轻松的看懂代码，如下图所示：

首先给出is_a_ge_zero_and_a_lt_b函数的定义及注释：

inline bool is_a_ge_zero_and_a_lt_b(int a, int b) {//若a大于等于零或小于b，返回true，否则返回false
  return static_cast(a) < static_cast(b);
}

该函数定义是：若a大于0且严格小于b，则返回真，否则返回假，该函数的作用是判断矩阵上某元的输出是否为pad的0。

然后给出im2col_cpu函数定义及注释：

/*im2col_cpu将c个通道的卷积层输入图像转化为c个通道的矩阵，矩阵的行值为卷积核高*卷积核宽，
也就是说，矩阵的单列表征了卷积核操作一次处理的小窗口图像信息；而矩阵的列值为卷积层
输出单通道图像高*卷积层输出单通道图像宽，表示一共要处理多少个小窗口。
im2col_cpu接收13个参数，分别为输入数据指针(data_im)，卷积操作处理的一个卷积组的通道
数(channels)，输入图像的高(height)与宽(width)，原始卷积核的高(kernel_h)与宽(kernel_w)，
输入图像高(pad_h)与宽(pad_w)方向的pad，卷积操作高(stride_h)与宽(stride_w)方向的步长，
卷积核高(stride_h)与宽(stride_h)方向的扩展，输出矩阵数据指针(data_col)*/
template 
void im2col_cpu(const Dtype* data_im, const int channels,
    const int height, const int width, const int kernel_h, const int kernel_w,
    const int pad_h, const int pad_w,
    const int stride_h, const int stride_w,
    const int dilation_h, const int dilation_w,
    Dtype* data_col) {
  const int output_h = (height + 2 * pad_h -
    (dilation_h * (kernel_h - 1) + 1)) / stride_h + 1;//计算卷积层输出图像的高
  const int output_w = (width + 2 * pad_w -
    (dilation_w * (kernel_w - 1) + 1)) / stride_w + 1;//计算卷积层输出图像的宽
  const int channel_size = height * width;//计算卷积层输入单通道图像的数据容量
  /*第一个for循环表示输出的矩阵通道数和卷积层输入图像通道是一样的，每次处理一个输入通道的信息*/
  for (int channel = channels; channel--; data_im += channel_size) {
	/*第二个和第三个for循环表示了输出单通道矩阵的某一列，同时体现了输出单通道矩阵的行数*/
    for (int kernel_row = 0; kernel_row < kernel_h; kernel_row++) {
      for (int kernel_col = 0; kernel_col < kernel_w; kernel_col++) {
        int input_row = -pad_h + kernel_row * dilation_h;//在这里找到卷积核中的某一行在输入图像中的第一个操作区域的行索引
		/*第四个和第五个for循环表示了输出单通道矩阵的某一行，同时体现了输出单通道矩阵的列数*/
        for (int output_rows = output_h; output_rows; output_rows--) {
          if (!is_a_ge_zero_and_a_lt_b(input_row, height)) {//如果计算得到的输入图像的行值索引小于零或者大于输入图像的高(该行为pad)
            for (int output_cols = output_w; output_cols; output_cols--) {
              *(data_col++) = 0;//那么将该行在输出的矩阵上的位置置为0
            }
          } else {
            int input_col = -pad_w + kernel_col * dilation_w;//在这里找到卷积核中的某一列在输入图像中的第一个操作区域的列索引
            for (int output_col = output_w; output_col; output_col--) {
              if (is_a_ge_zero_and_a_lt_b(input_col, width)) {//如果计算得到的输入图像的列值索引大于等于于零或者小于输入图像的宽(该列不是pad)
                *(data_col++) = data_im[input_row * width + input_col];//将输入特征图上对应的区域放到输出矩阵上
              } else {//否则，计算得到的输入图像的列值索引小于零或者大于输入图像的宽(该列为pad)
                *(data_col++) = 0;//将该行该列在输出矩阵上的位置置为0
              }
              input_col += stride_w;//按照宽方向步长遍历卷积核上固定列在输入图像上滑动操作的区域
            }
          }
          input_row += stride_h;//按照高方向步长遍历卷积核上固定行在输入图像上滑动操作的区域
        }
      }
    }
  }
}

接下来我们举个例子，并展示具体操作流程：

im2col_cpu函数将卷积层输入转化为矩阵相乘的右元，核心是5个for循环，首先第一个for循环表示按照输入的通道数逐个处理卷积层输入的特征图，下面笔者将用图示表示剩余的四个for循环操作，向读者朋友们展示卷积层输入的单通道特征图是通过怎样的方式转化为一个矩阵。在这里我们假设，卷积层输入单通道特征图原大小为5*5，高和宽方向的pad为1，高和宽方向步长为2，卷积核不进行扩展。

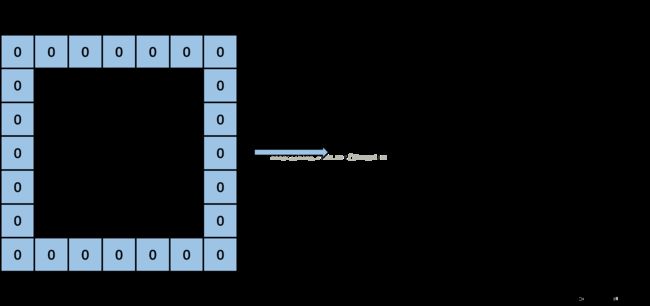
   我们先计算一下，卷积层输入单通道特征图转化得到的矩阵的尺度，矩阵的行数应该为卷积核高*卷积核宽，即为9，列数应该为卷积层输出特征图高(output_h)*卷积层输出特征图宽(output_w)，也为9，那么，im2col算法起始由下图开始：

首先kernel_row为0，kernel_col也为0。按照input_row = -pad_h + kernel_row * dilation_h计算input_row的值，在这里，pad_h为1，kernel_row为0，dilation_h为1，计算出input_row为-1，此时output_row为3，满足函数中的第一个if条件，那么在输出图像上先置output_w个零，因为output_w为3，因此得到下图：

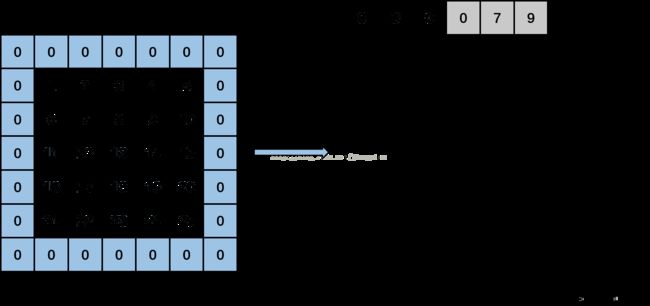
然后input_row加上步长2，由-1变成1，此时output_rows为2，计算input_col等于-1，此时执行input_col定义下面的for循环，得到3个值：依次往目标矩阵中填入0，data_im[1*5+1]和data_im[1*5+3]，即填入0,7和9。得到下图：

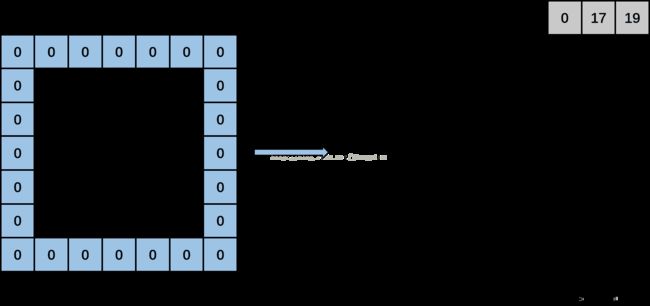
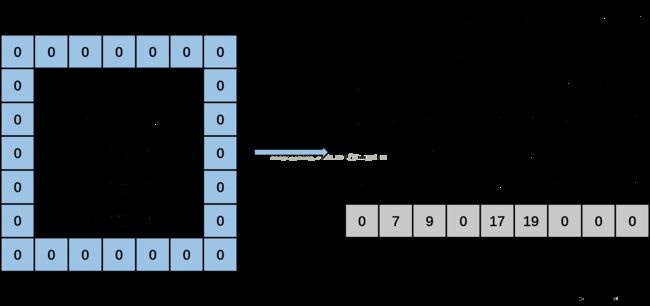
再接着执行，此时input_row再加上2变为3，此时output_rows变为1，计算input_col等于-1，执行input_col定义下面的for循环，得到3个值，分别为0，data_im[3*5+1]和data_im[3*5+3]，即填入0,17和19。得到下图：

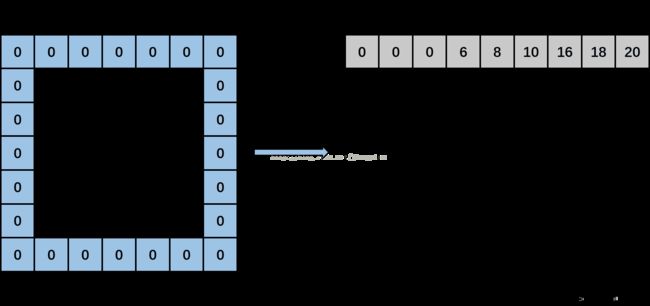
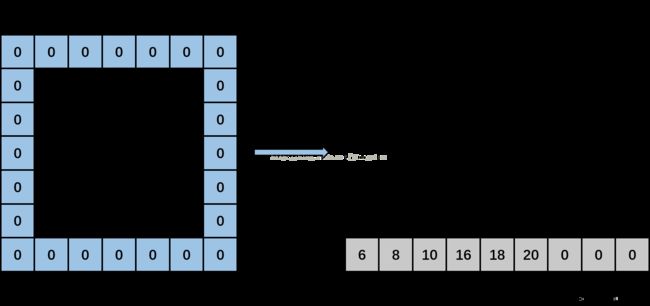
   接着，kernel_col变成1，此时kernel_row为0，kernel_col为1。计算input_row又变成-1，第一个if条件成立，那么，再在输出矩阵上输出3个0。然后，input_row变成1，input_col分别为0(-1+1)，2(-1+1+2)和4(-1+1+2+2)时，输出矩阵上分别输出data_im[1*5+0]，data[1*5+2]，data[1*5+4]，即分别填入6,8,10。然后，input_row变成3，input_col分别为0，2，4时，输出矩阵上分别输出data_im[3*5+0]，data[3*5+2]，data[3*5+4]，即分别输出16,18,20。

   然后，kernel_col变成2，此时kernel_row为0，kernel_col为2。计算input_row又变成-1，第一个if条件成立，那么，再在输出矩阵上输出3个0。然后，input_row变成1，input_col分别为1(-1+2)，3(-1+2+2)和5(-1+2+2+2)时，输出矩阵上分别输出data_im[1*5+1]，data[1*5+3]，0，即分别填入7,9,0。然后，input_row变成3，input_col分别为1，3，5时，输出矩阵上分别输出data_im[3*5+0]，data[3*5+2]，0，即分别输出17,19,0。见下图：

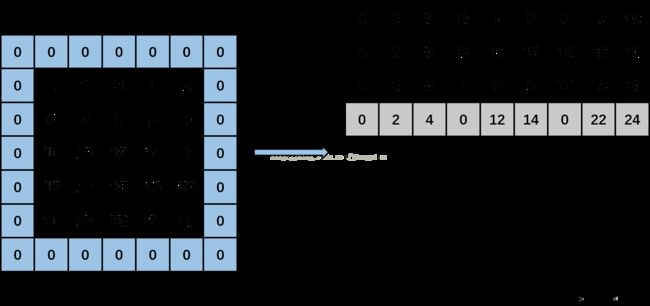
   接着，kernel_row变成1，kernel_col变成0。计算input_row又变成0，input_col分别为-1(-1+0)，1(-1+0+2)和3(-1+0+2+2)，输出矩阵上分别输出0，data[0*5+1]，data[0*5+3]，即分别填入0,2,4。然后，input_row变成2，input_col分别为-1，1和3时，输出矩阵上分别输出0，data[2*5+1]，data[2*5+3]，即分别填入0,12,14。然后，input_row变成4，input_col分别为-1，1，3时，输出矩阵上分别输出0，data[4*5+1]，data[4*5+3]，即分别输出0,22,24。见下图：

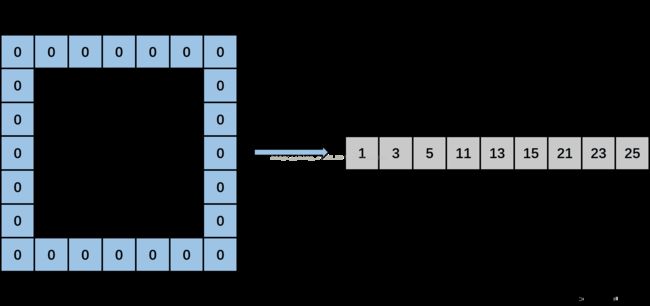
   然后，kernel_row为1，kernel_col变成1。计算input_row为0，input_col分别为0(-1+1)，2(-1+1+2)和4(-1+1+2+2)，输出矩阵上分别输出data[0*5+0]，data[0*5+2]，data[0*5+4]，即分别填入1,3,5。然后，input_row变成2，input_col分别为0，2和4时，输出矩阵上分别输出data[2*5+0]，data[2*5+2]，data[2*5+4]，即分别填入11,13,15。然后，input_row变成4，input_col分别为0，2，4时，输出矩阵上分别输出data[4*5+0]，data[4*5+2]，data[4*5+4]，即分别输出21,23,25。见下图：

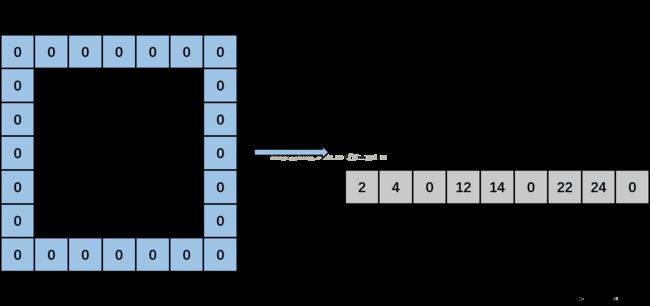
   然后，kernel_row为1，kernel_col变成2。计算input_row为0，input_col分别为1(-1+2)，3(-1+2+2)和5(-1+2+2+2)，输出矩阵上分别输出data[0*5+1]，data[0*5+3]，0，即分别填入2,4,0。然后，input_row变成2，input_col分别为1，3和5时，输出矩阵上分别输出data[2*5+1]，data[2*5+3]，0，即分别填入12,14,0。然后，input_row变成4，input_col分别为1，3，5时，输出矩阵上分别输出data[4*5+1]，data[4*5+3]，0，即分别输出22,24,0。见下图：

   接着，kernel_row变成2，kernel_col变成0。计算input_row为1，input_col分别为-1(-1+0)，1(-1+0+2)和3(-1+0+2+2)，输出矩阵上分别输出0，data[1*5+1]，data[1*5+3]，即分别填入0,7,9。然后，input_row变成3，input_col分别为-1，1和3时，输出矩阵上分别输出0，data[3*5+1]，data[3*5+3]，即分别填入0,17,19。然后，input_row变成5，满足第一个if条件，直接输出三个0。见下图：

   然后，kernel_row为2，kernel_col变成1。计算input_row为1，input_col分别为0(-1+1)，2(-1+1+2)和4(-1+1+2+2)，输出矩阵上分别输出data[1*5+0]，data[1*5+2]，data[1*5+4]，即分别填入6,8,10。然后，input_row变成3，input_col分别为0，2和4时，输出矩阵上分别输出data[3*5+0]，data[3*5+2]，data[3*5+4]，即分别填入16,18,20。然后，input_row变成5，满足第一个if条件，直接输出三个0。见下图：

   最后，kernel_row为2，kernel_col变成2。计算input_row为1，input_col分别为1(-1+2)，3(-1+2+2)和5(-1+2+2+2)，输出矩阵上分别输出data[1*5+1]，data[1*5+3]，0，即分别填入7,9,0。然后，input_row变成3，input_col分别为1，3和5时，输出矩阵上分别输出data[3*5+1]，data[3*5+3]，0，即分别填入17,19,0。然后，input_row变成5，满足第一个if条件，直接输出三个0。见下图：

   到此卷积层单通道输入特征图就转化成了一个矩阵，请读者朋友们仔细看看，矩阵的各列是不是卷积核操作的各小窗口呢？

   笔者还想提醒大家的是，注意卷积中的zero-pad操作的实现，并不是真正在原始输入特征图周围添加0，而是在特征图转化得到的矩阵上的对应位置添加0。

   而im2col_cpu函数功能的相反方向的实现则有由col2im_cpu函数完成，笔者依旧把该函数的代码注释放在下面：

/*col2im_cpu为im2col_cpu的逆操作接收13个参数，分别为输入矩阵数据指针(data_col)，卷积操作处理的一个卷积组的通道
数(channels)，输入图像的高(height)与宽(width)，原始卷积核的高(kernel_h)与宽(kernel_w)，
输入图像高(pad_h)与宽(pad_w)方向的pad，卷积操作高(stride_h)与宽(stride_w)方向的步长，
卷积核高(stride_h)与宽(stride_h)方向的扩展，输出图像数据指针(data_im)*/
template 
void col2im_cpu(const Dtype* data_col, const int channels,
    const int height, const int width, const int kernel_h, const int kernel_w,
    const int pad_h, const int pad_w,
    const int stride_h, const int stride_w,
    const int dilation_h, const int dilation_w,
    Dtype* data_im) {
  caffe_set(height * width * channels, Dtype(0), data_im);//首先对输出的区域进行初始化，全部填充0
  const int output_h = (height + 2 * pad_h -
    (dilation_h * (kernel_h - 1) + 1)) / stride_h + 1;//计算卷积层输出图像的宽
  const int output_w = (width + 2 * pad_w -
    (dilation_w * (kernel_w - 1) + 1)) / stride_w + 1;//计算卷积层输出图像的高
  const int channel_size = height * width;//col2im输出的单通道图像容量
  for (int channel = channels; channel--; data_im += channel_size) {//按照输出通道数一个一个处理
    for (int kernel_row = 0; kernel_row < kernel_h; kernel_row++) {
      for (int kernel_col = 0; kernel_col < kernel_w; kernel_col++) {
        int input_row = -pad_h + kernel_row * dilation_h;//在这里找到卷积核中的某一行在输入图像中的第一个操作区域的行索引
        for (int output_rows = output_h; output_rows; output_rows--) {
          if (!is_a_ge_zero_and_a_lt_b(input_row, height)) {//如果计算得到的输入图像的行值索引小于零或者大于输入图像的高(该行为pad)
            data_col += output_w;//那么，直接跳过这output_w个数，这些数是输入图像第一行上面或者最后一行下面pad的0
          } else {
            int input_col = -pad_w + kernel_col * dilation_w;//在这里找到卷积核中的某一列在输入图像中的第一个操作区域的列索引
            for (int output_col = output_w; output_col; output_col--) {
              if (is_a_ge_zero_and_a_lt_b(input_col, width)) {//如果计算得到的输入图像的列值索引大于等于于零或者小于输入图像的宽(该列不是pad)
                data_im[input_row * width + input_col] += *data_col;//将矩阵上对应的元放到将要输出的图像上
              }//这里没有else，因为如果紧挨的if条件不成立的话，input_row * width + input_col这个下标在data_im中不存在，同时遍历到data_col的对应元为0
              data_col++;//遍历下一个data_col中的数
              input_col += stride_w;//按照宽方向步长遍历卷积核上固定列在输入图像上滑动操作的区域
            }
          }
          input_row += stride_h;//按照高方向步长遍历卷积核上固定行在输入图像上滑动操作的区域
        }
      }
    }
  }
}

这里重点提一下，我觉得这段代码真正让我觉得艺术的地方在于，im2col和col2im的代码几乎一样，只是非常少的部分赋值变了。这逻辑我是一下想不出来。。。

到此，im2col.cpp中的核心函数就已经解析完毕了，笔者在最开始阅读这个源码的时候，也没有弄得太明白，可是经过仔细画图推敲，明白了其中的含义。从这件小事可以看出，光看不练假把式，在阅读源码时，遇到功能实现中比较抽象的部分，应该再仔细思考分析的同时，多动笔杆，切勿偷懒！

https://blog.csdn.net/dwyane12138/article/details/78449898

https://blog.csdn.net/jiongnima/article/details/69736844

https://www.cnblogs.com/hdk1993/p/8893944.html（python实现）