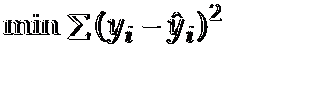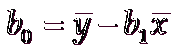机器学习快速入门

1、课程介绍

• 学习前提 
  • 对微积分，线性代数，概率论的基本知识有一定了解
  • 有一定编程基础（最好是Python）
• 学习目标 
  • 理解机器学习的概念、原理、常用算法
  • 学会对原始数据的预处理
  • 学会使用Python语言和相关的机器学习库
  • 学会使用常用算法和应用框架解决实际问题
• 课程安排 
  • 基本介绍
  • 基本概念
  • 监督学习
  • 非监督学习

2、机器学习

• 概念 
  • 多领域交叉学科，涉及概率论、统计学、逼近论、算法复杂度理论等多门学科。专门研究计算机模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能。
  • 学科定位 
    人工智能(Artificial Intelligence, AI）的核心，是使计算机具有智能的根本途径，其应用遍及人工智能的各个领域.。
• 定义 
  • 探究和开发一系列算法来如何使计算机不需要通过外部明显的指示，而可以自己通过数据来学习，建模，并且利用建好的模型和新的输入来进行预测的学科。
  • 几个经典定义： 
    • 阿瑟·萨缪尔(Arthur Samuel (1959)): 一门不需要通过外部程序指示而让计算机有能力自我学习的学科
    • Langley（1996) ： “机器学习是一门人工智能的科学，该领域的主要研究对象是人工智能，特别是如何在经验学习中改善具体算法的性能”
    • 汤姆·米切尔(Tom Michell)  (1997): “机器学习是对能通过经验自动改进的计算机算法的研究”
• 学习 
  • 针对经验E (experience) 和一系列的任务 T (tasks) 和一定表现的衡量 P，如果随之经验E的积累，针对定义好的任务T可以提高表现P，就说计算机具有学习能力。

例子： 下棋，语音识别，自动驾驶汽车等。

3、机器学习的应用

• 自动驾驶、无人机、语音识别、语言翻译、识别垃圾邮件、推荐系统

4、深度学习（Deep Learning）

1. 什么是深度学习？

深度学习是基于机器学习延伸出来的一个新的领域，由以人大脑结构为启发的神经网络算法为起源加之模型结构深度的增加发展，并伴随大数据和计算能力的提高而产生的一系列新的算法。

2. 深度学习什么时间段发展起来的？

其概念由著名科学家Geoffrey Hinton( 杰弗里·辛顿)等人在2006年和2007年在《Sciences》等上发表的文章被提出和兴起。

3. 深度学习能用来干什么？为什么近年来引起广泛的关注？

深度学习，作为机器学习中延伸出来的一个领域，被应用在图像处理与计算机视觉，自然语言（翻译）处理以及语音识别等领域。自2006年至今，学术界和工业界合作在深度学习方面的研究与应用在以上领域取得了突破性的进展。以ImageNet为数据库的经典图像（1000多种图像）中的物体识别竞赛为例，击败了所有传统算法，取得了前所未有的精确度。

4. 深度学习目前有哪些代表性的学术机构和公司走在前沿？人才需要如何？

学校以多伦多大学（hinton:），纽约大学，斯坦福大学为代表，工业界以Google, Facebook, 和百度为代表走在深度学习研究与应用的前沿。Google挖走了Hinton(杰弗里·辛顿)，Facebook挖走了LeCun(延恩·勒昆)，百度硅谷的实验室挖走了Andrew Ng(吴恩达)，Google去年4月份以超过5亿美金收购了专门研究深度学习的初创公司DeepMind, 深度学习方因技术的发展与人才的稀有造成的人才抢夺战达到了前所未有激烈的程度。诸多的大大小小(如阿里巴巴，雅虎）等公司也都在跟进，开始涉足深度学习领域，深度学习人才需求量会持续快速增长。

5. 深度学习如今和未来将对我们生活造成怎样的影响？

目前我们使用的Android手机中google的语音识别，百度识图，google的图片搜索，都已经使用到了深度学习技术。Facebook在去年名为DeepFace的项目中对人脸识别的准确率第一次接近人类肉眼（97.25% vs 97.5%)。大数据时代，结合深度学习的发展在未来对我们生活的影响无法估量。保守而言，很多目前人类从事的活动都将因为深度学习和相关技术的发展被机器取代，如自动汽车驾驶，无人飞机，以及更加职能的机器人等。深度学习的发展让我们第一次看到并接近人工智能的终极目标。

机器学习的基本概念

训练集、测试集、验证集、特征值、监督学习、非监督学习、半监督学习、分类、回归

概念学习：人类学习概念：鸟、车、计算机

  定义：概念学习是指从有关某个布尔函数的输入输出训练样例中推断该布尔函数

 

从一个小例子更好地理解这些概念

我们从“小明进行水上运动，是否享受运动取决于许多因素”这个例子入手理解机器学习的一些基本概念，如下图。

 

每一行数据（一天）称为一个实例（instance），记为x

每个实例的属性值由天气，温度，湿度，风力，水温，预报6个属性表示

所有实例的集合（四天），称为样例，记为X

待学习的目标函数称为目标概念（target concept), 记做c。

当享受运动时，记c(x) = 1

当不享受运动时，记c(x) = 0

c(x)也可叫做y

学习目标：f: X -> Y

其实说白了，就是让我们根据“输入的属性值”和“输出的是否享受运动值”，找到两者之间的关系，也就是函数表达式f。即满足什么样的属性组合时，小明享受运动。

 

论文中常见的概念

训练集(training set/data)/训练样例（training examples): 
用来进行训练，也就是产生模型或者算法的数据集

测试集(testing set/data)/测试样例 (testing examples)： 
用来专门进行测试已经学习好的模型或者算法的数据集

特征向量(features/feature vector)： 
属性的集合，通常用一个向量来表示，附属于一个实例

标记(label): 
c(x), 实例类别的标记，即上边例子中的是否享受运动的“是”与“否”

正例(positive example)：“享受运动” 
反例(negative example)：“不享受运动”

 

例子：研究美国硅谷房价

 

分类 (classification): 目标标记为类别型数据(category) 
即上面小明的例子，享受运动的“是”与“否”

回归(regression): 目标标记为连续性数值 (continuous numeric value) 
即该例中的“房价”

 

例子：研究肿瘤良性恶性与尺寸颜色的关系

特征值：肿瘤尺寸，颜色 
标记：良性/恶性

有监督学习(supervised learning)： 训练集有类别标记(class label) 
上面“小明”和“房价”的例子都是有监督学习，因为不管是离散的值“是”与“否”还是连续的房价，c(x)都是已知的

无监督学习(unsupervised learning)： 无类别标记(class label) 
“肿瘤”的例子是无监督的学习，c(x)未知

半监督学习（semi-supervised learning)： 
有类别标记的训练集 + 无标记的训练集

 

机器学习的步骤

1）把数据拆分为训练集和测试集 
2）用训练集和训练集的特征向量来训练算法 
3）用学习来的算法运用在测试集上来评估算法——可能要涉及到调整参数（parameter tuning), 用验证集（validation set）：用于调参数的集合

简单线性回归（上）---监督学习，回归类

0. 前提介绍：

为什么需要统计量？ 
统计量：描述数据特征

0.1 集中趋势衡量

0.1.1均值（平均数，平均值）（mean）

 

{6, 2, 9, 1, 2}

(6 + 2 + 9 + 1 + 2) / 5 = 20 / 5 = 4

0.1.2中位数 （median）:

将数据中的各个数值按照大小顺序排列，居于中间位置的变量

给数据排序：1， 2， 2， 6， 9 
找出位置处于中间的变量：2

当n为寄数的时候：直接取位置处于中间的变量 
当n为偶数的时候，取中间两个量的平均值

0.1.3众数 （mode）：

数据中出现次数最多的数

0.2 离散程度衡量(一组数离散度)

0.2.1 方差（variance)： 

 

{6, 2, 9, 1, 2}

(1) (6 - 4)^2 + (2 - 4) ^2 + (9 - 4)^2 + (1 - 4)^2 + (2 - 4)^2 
= 4 + 4 + 25 + 9 + 4 
= 46 
(2) n - 1 = 5 - 1 = 4 
(3) 46 / 4 = 11.5

0.2.2 标准差 (standard deviation)

 

s = sqrt(11.5) = 3.39

 

1. 介绍：

回归(regression)：Y变量为连续数值型(continuous numerical variable) （称之为回归）
如：房价，人数，降雨量 
分类(Classification)：Y变量为类别型(categorical variable) 
如：颜色类别，电脑品牌，有无信誉

 

2. 简单线性回归(Simple Linear Regression)

2.1 很多做决定的过程通常是根据两个或者多个变量之间的关系 
2.2 回归分析(regression analysis)：用来建立方程模拟两个或者多个变量之间如何关联 
2.3 被预测的变量叫做：因变量(dependent variable), y, 输出(output) 
2.4 被用来进行预测的变量叫做： 自变量(independent variable), x, 输入(input)

 

3. 简单线性回归介绍

3.1 简单线性回归包含一个自变量(x)和一个因变量(y) 
3.2 以上两个变量的关系用一条直线来模拟 
3.3 如果包含两个以上的自变量，则称作多元回归分析(multiple regression)

 

4. 简单线性回归模型

4.1 被用来描述因变量(y)和自变量(X)以及偏差(error)之间关系的方程叫做回归模型 
4.2 简单线性回归的模型是:

 

其中：β0与β1被称为参数（决定了y与x的关系）， ε被称为偏差（随机因素的值，满足正态分布，均值为零）

 

5. 简单线性回归方程

对回归模型两边求期望（均值），得到： 
E(y) = β0+β1x 
这个方程对应的图像是一条直线，称作回归线。其中，β0是回归线的截距，β1是回归线的斜率。E(y)是在一个给定x值下y的期望值（均值）。

 

6. 正向线性关系：（x变大，E（y）也变大）

 

7. 负向线性关系：（x变大，E（x）变小）

 

8. 无关系：（截距存在，E(x)不受x影响）

 

9. 估计的简单线性回归方程

ŷ=b0+b1x 
这个方程叫做估计线性方程(estimated regression line) ，做训练时，我并不知道真实结果是什么，所以，叫估计值。
其中，b0是估计线性方程的纵截距，b1是估计线性方程的斜率，ŷ是在自变量x等于一个给定值的时候，y的估计值。

 

10. 线性回归分析流程：

左边是一个回归方程，我们的目的就是估计B0,B1，只要估计出这个值，我们就知道，未来数据关系。那么如何估计呢，可以用Sample数据。如果有全部数据B0与B1有一种真实关系

在估计b0,b1时，我们可以使用估计方程。

 

11. 关于偏差ε的假定（使用简单线性回归要做以下假设）

11.1 ε是一个随机的变量，均值为0 
11.2 ε的方差(variance)对于所有的自变量x是一样的 
11.3 ε的值是独立的 
11.4 ε满足正态分布

 

简单线性回归（下）

 

1. 简单线性回归模型举例：

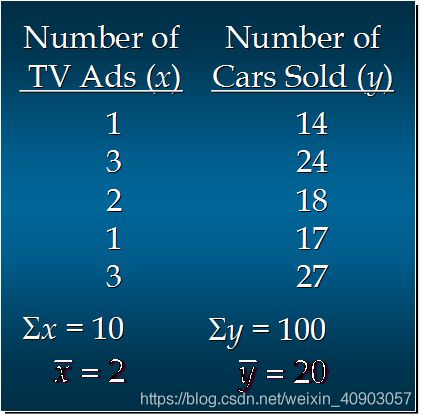
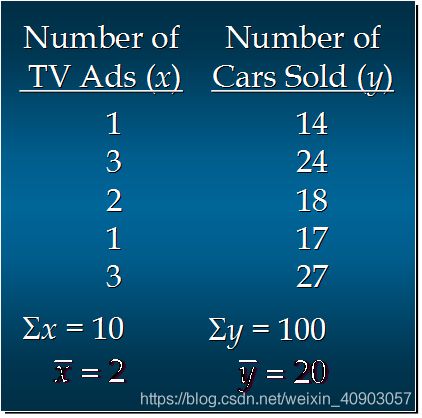
汽车卖家做电视广告数量与卖出的汽车数量：(以下是5个月数据，因为只有一个自变量，所以我们可以使用简单线性回归来分析预测)

 

1.1 如何画出适合简单线性回归模型的最佳回归线？（我们可以用上边数据画出5个月的点，横代表广告数，y代表汽车数量，我们要找出一个回归线，最能代表这些点趋势的一个直线，所谓最好就是图上的每个点离直线最近）

 

 

使sum of squares最小（如果满足这个条件，那么这个条直线就是最好的，yi指是每个点的y值，y hat指的是直线上的点，比如：当x为2时，对应直线上的值）

计算过程

 

 

 

分子 = (1-2)(14-20)+(3-2)(24-20)+(2-2)(18-20)+(1-2)(17-20)+(3-2)(27-20) 
= 6 + 4 + 0 + 3 + 7 
= 20

分母 = （1-2）^2 + (3-2)^2 + (2-2)^2 + (1-2)^2 + (3-2)^2 
= 1 + 1 + 0 + 1 + 1 
= 4

b1 = 20/4 =5

b0 = 20 - 5*2 = 20 - 10 = 10

1.2 预测：

假设有一周广告数量为6，预测的汽车销售量是多少？

 

x_given = 6

Y_hat = 5*6 + 10 = 40

1.3 Python实现：

测试代码：

import numpy as np

 

def fitSLR(x,y):

    n = len(x)

    denominator = 0

    numerator = 0

    for i in range(0,n):

        numerator += (x[i] - np.mean(x))*(y[i] - np.mean(y))

        denominator += (x[i] - np.mean(x))**2

 

    print("numerator: "+str(numerator))

    print("denominator: "+str(denominator))

    b1 = numerator/float(denominator)

    b0 = np.mean(y) - b1*np.mean(x)

 

    return b0,b1

 

def predict(x,b0,b1):

    return b0+x*b1

 

x = [1,3,2,1,3]

y = [14,24,18,17,27]

 

b0,b1 = fitSLR(x,y)

 

print("intercept: "+str(b0))

print("slope: "+str(b1))

 

x_test = 6

y_test = predict(x_test,b0,b1)

 

print("y_test: "+str(y_test))

 

测试结果：

numerator: 20.0

denominator: 4.0

intercept: 10.0

slope: 5.0

y_test: 40.0

作业：案例数据很好理解，是常见的销售数据，反映的是某公司太阳镜一年12个月的具体销售情况。试分析当广告费用为15万元时，预测当月的销售量值。

 

邻近算法—监督学习，分类算法

1. 综述：

1.1 Cover和Hart在1968年提出了最初的邻近算法 
1.2 KNN算法属于分类(classification)算法 
1.3 输入基于实例的学习(instance-based learning), 懒惰学习(lazy learning)：不建模型，在做测试时，才根据训练集进行归类。就像学生学习，在考试时，才学习。

2. 例子：需求：根据一部分电影实例，想推断出一部新电影是属于哪一种电影（爱情，动作），为了达到这种需求，我们可以从实例中抽出特征值，以特征值为x,y。

 

未知电影属于什么类型？（我们可以某个实例电影模拟成实例点，也可以是多维的，如果是多维的我们可以把点想成，多维空间中的点，在这里是二维的）

 

这种问题如何用KNN算法解决呢？我们可以根据一个未知点，与训练集中某个点最近，我们就可以，判断未知点类型。

 

 

3. 算法详述：

3.1 步骤：

1 为了判断未知实例的类别，以所有已知类别的实例作为参照 （以已知训练集为考）
2 选择参数K （选择与未知点最近参考实例个数，k值一般不会太大1，3，5，7）
3 计算未知实例与所有已知实例的距离（计算未知点与所有训练集点距离） 
4 选择最近K个已知实例 （选择k个最近点）
5 根据少数服从多数的投票法则(majority-voting)，让未知实例归类为K个最邻近样本中最多数的类别（在k个最近点中，根据少数服从多数原则来确定未知点类型）

3.2 细节:

关于K（一般取奇数） 
关于距离的衡量方法: 
3.2.1 Euclidean Distance 定义

二维距离计算： （这个计算可以适合于多维的，只要对应维度相减就可以）

n维距离计算： 

其他距离衡量： 
余弦值（cos）, 相关度 （correlation）, 曼哈顿距离 （Manhattan distance）

3.3 举例：？号那个实例规哪一个呢，如果k为1，k为4,k为9，会发现一个规律，KNN算法，对k值敏感，为1时，噪音比较大。通常通过增大k，来减小噪音的影响。

 

4. 算法优缺点：

4.1 算法优点

简单 
易于理解 
容易实现 
通过对K的选择可具备丢噪音数据的健壮性

4.2 算法缺点

需要大量空间储存所有已知实例 
算法复杂度高（需要比较所有已知实例与要分类的实例） 
当其样本分布不平衡时，比如其中一类样本过大（实例数量过多）占主导的时候，新的未知实例容易被归类为这个主导样本（下面Y点如果k为7，那么Y将归为蓝色点，实际应该为红），因为这类样本实例的数量过大，但这个新的未知实例实际并未接近目标样本

 

5. 改进版本

考虑距离，根据距离加上权重 ,把距离也考虑进去，如果距离小，权重比较大，那么就能避免一些问题
比如: 1/d (d: 距离）

 

KNN算法下

   需求：需要把150花实例，进行分类。

  1 Iris Plants Database介绍：

虹膜

150个实例

特征值（4种）： 
萼片长度，萼片宽度，花瓣长度，花瓣宽度 
(sepal length, sepal width, petal length and petal width）

类别（3类）： 
Iris setosa, Iris versicolor, Iris virginica.

 

2. KNN实现（利用sklearn机器学习库）:

from sklearn import neighbors

from sklearn import datasets

 

# get knn algorithm

knn = neighbors.KNeighborsClassifier()

# get iris datasets

iris = datasets.load_iris()

 

print(iris)

 

# use knn build the model

knn.fit(iris.data,iris.target)

 

# use the model to predict

predictedLabel = knn.predict([[0.1,0.2,0.3,0.4]])

print(predictedLabel)

3.KNN实现（不用sklearn机器学习库）

# Example of knn implemented in Python

 

import csv

import random

import math

import operator

 

def loadDataset(filename, split, trainingSet=[] , testSet=[]):

    with open(filename, 'r') as csvfile:

        lines = csv.reader(csvfile)

        dataset = list(lines)

# print("dataset: "+str(dataset))

# print("type of dataset[0][0]: "+str(type(dataset[0][0])))

# print("length of dataset: "+str(len(dataset)))

        for x in range(len(dataset)):

            for y in range(4):

                dataset[x][y] = float(dataset[x][y])

            if random.random() < split:

                trainingSet.append(dataset[x])

            else:

                testSet.append(dataset[x])

 

def euclideanDistance(instance1, instance2, length):

    distance = 0

    for x in range(length):

        distance += pow((instance1[x] - instance2[x]), 2)

    return math.sqrt(distance)

 

def getNeighbors(trainingSet, testInstance, k):

    distances = []

# print("testInstance: "+str(len(testInstance)))

    length = len(testInstance)-1

# print("trainingSet: "+str(len(trainingSet)))

    for x in range(len(trainingSet)):

        dist = euclideanDistance(testInstance, trainingSet[x], length)

        distances.append((trainingSet[x], dist))

    distances.sort(key=operator.itemgetter(1))

    neighbors = []

    for x in range(k):

        neighbors.append(distances[x][0])

    return neighbors

 

def getResponse(neighbors):

    classVotes = {}

    for x in range(len(neighbors)):

# print("neighbors[x][-1]:"+str(neighbors[x][-1]))

        response = neighbors[x][-1]

        if response in classVotes:

            classVotes[response] += 1

        else:

            classVotes[response] = 1

    sortedVotes = sorted(classVotes.items(), key=operator.itemgetter(1), reverse=True)

    return sortedVotes[0][0]

 

def getAccuracy(testSet, predictions):

    correct = 0

    for x in range(len(testSet)):

        if testSet[x][-1] == predictions[x]:

            correct += 1

    return (correct/float(len(testSet))) * 100.0

 

def main():

    # prepare data

    trainingSet=[]

    testSet=[]

    split = 0.67

    loadDataset(r'D:\eclipse\mars\project\DeepLearningBasicsMachineLearning\Datasets\iris.data.txt', split, trainingSet, testSet)

    print ('Train set: ' + repr(len(trainingSet)))

    print ('Test set: ' + repr(len(testSet)))

    # generate predictions

    predictions=[]

    k = 3

    for x in range(len(testSet)):

        neighbors = getNeighbors(trainingSet, testSet[x], k)

        result = getResponse(neighbors)

        predictions.append(result)

        print('> predicted=' + repr(result) + ', actual=' + repr(testSet[x][-1]))

    accuracy = getAccuracy(testSet, predictions)

    print('Accuracy: ' + repr(accuracy) + '%')

 

main()

作业：根据一部分电影实例，求出未知实例

 

聚类之K-means算法（上）-非监督学习 (unsupervised learning)  分类

1. 归类：

聚类(clustering) 属于非监督学习 (unsupervised learning) 
无类别标记(class label)

2. 举例：横轴代表直径 纵代表周长 ,对肿瘤进行归类，我们并不知知谁是恶性，谁是良性，只知道里面的点。然后利用周长和直径进行归类。

 

3. K-means 算法：

3.1 Clustering 中的经典算法，数据挖掘经典算法之一。

3.2 算法接受参数 k（表示总体样本分几类） ；然后将事先输入的n个数据对象划分为 k个聚类，以便使得所获得的聚类满足：同一聚类中的对象相似度较高；而不同聚类中的对象相似度较小。（如上图，所有蓝色在一起，所有绿色都在一起。在一起的，相似度高。两类之间，相似度低。）

3.3 算法思想： 
以空间中k个点为中心进行聚类，对最靠近他们的对象归类。通过迭代的方法，逐次更新各聚类中心的值，直至得到最好的聚类结果。（先选取k个点，以这三个点为中心，进行归类，因为这三个点随便选的，所以归类结果不准，然后，再按照算法，再选取三个点，再归类，就这样循环，直到归类成功）

3.4 算法描述： 
（1）适当选择c个类的初始中心； 
（2）在第k次迭代中，对任意一个样本，求其到c各中心的距离，将该样本归到距离最短的中心所在的类；（计算所有样本到中心点距离，看所有样本到哪个中心最近，就归为哪一类，形成初步分类） 
（3）利用均值等方法更新该类的中心值；（经过第二步已经形成初步分类，根据三个分类，求每个分类均值，这样又形成三个中心点） 
（4）对于所有的c个聚类中心，如果利用（2）（3）的迭代法更新后，值保持不变，则迭代结束，否则继续迭代。

3.5 算法流程：描述下算法详细流程

 

输入：k, data[n]; （输入k值 和数据）
（1） 选择k个初始中心点，例如c[0]=data[0],…c[k-1]=data[k-1]; 
（2） 对于data[0]….data[n], 分别与c[0]…c[k-1]比较，假定与c[i]差值最少，就标记为i; 
（3） 对于所有标记为i点，重新计算c[i]={ 所有标记为i的data[j]之和}/标记为i的个数； 
（4） 重复(2)(3),直到所有c[i]值的变化小于给定阈值。

4. 举例：

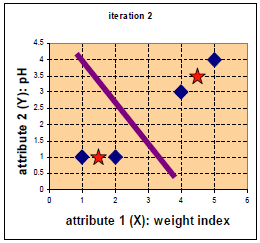
下例以重量和ph值来进行聚类，分成两类。我们可以重量为x,以ph为y

 

D0表示第一次循环，第一行表示，第一个点到第一个中心点距离，第二个点到第一个中心距离……直到第四个点到第一个中心点距离。

第二行表示,第一个点到第二个中心点距离，第二个点到第二个中心点距离…..

第二个矩阵：表示每个点坐标。

 

第三个矩阵：表示第一轮循环后的分级，通过对比距离。第一组只有一个点。第二组有三个点。

 

C2表示均值：因为第一个中心点就一个，所以中心点扔然是(1,1),但是第二个中心点有三个点，所以需要所有点x相加/3,所有y相加/3,最后是(11/3,8/3),现在中心点变成(1,1), (11/3,8/3)

 

第二次循环

第二次循环后，发现变了，第一组多一个点。

重心求中心点变成(3/2,1),(4.5,3.5)

 

第三次循环

发现分组后，仍然和上一次一样，停止循环。分类结束

优点：速度快，简单 
缺点：最终结果跟初始点选择相关，容易陷入局部最优，需知到k值

 

 

 

 

 

 

聚类之K-means算法（下）

 

K-means算法实现代码：（接上一节的小例子，如图）

 

import numpy as np

 

# Function: K Means

# -------------

# K-Means is an algorithm that takes in a dataset and a constant

# k and returns k centroids (which define clusters of data in the

# dataset which are similar to one another).

def kmeans(X, k, maxIt):

 

    numPoints, numDim = X.shape

 

    dataSet = np.zeros((numPoints, numDim + 1))

    dataSet[:, :-1] = X

 

    # Initialize centroids randomly

    centroids = dataSet[np.random.randint(numPoints, size = k), :]

    centroids = dataSet[0:2, :]

    #Randomly assign labels to initial centorid

    centroids[:, -1] = range(1, k +1)

 

    # Initialize book keeping vars.

    iterations = 0

    oldCentroids = None

 

    # Run the main k-means algorithm

    while not shouldStop(oldCentroids, centroids, iterations, maxIt):

        print ("iteration: \n", str(iterations))

        print ("dataSet: \n", str(dataSet))

        print ("centroids: \n", str(centroids))

        # Save old centroids for convergence test. Book keeping.

        oldCentroids = np.copy(centroids)

        iterations += 1

 

        # Assign labels to each datapoint based on centroids

        updateLabels(dataSet, centroids)

 

        # Assign centroids based on datapoint labels

        centroids = getCentroids(dataSet, k)

 

    # We can get the labels too by calling getLabels(dataSet, centroids)

    return dataSet

# Function: Should Stop

# -------------

# Returns True or False if k-means is done. K-means terminates either

# because it has run a maximum number of iterations OR the centroids

# stop changing.

def shouldStop(oldCentroids, centroids, iterations, maxIt):

    if iterations > maxIt:

        return True

    return np.array_equal(oldCentroids, centroids)  

# Function: Get Labels

# -------------

# Update a label for each piece of data in the dataset.

def updateLabels(dataSet, centroids):

    # For each element in the dataset, chose the closest centroid.

    # Make that centroid the element's label.

    numPoints, numDim = dataSet.shape

    for i in range(0, numPoints):

        dataSet[i, -1] = getLabelFromClosestCentroid(dataSet[i, :-1], centroids)

 

 

def getLabelFromClosestCentroid(dataSetRow, centroids):

    label = centroids[0, -1];

    minDist = np.linalg.norm(dataSetRow - centroids[0, :-1])

    for i in range(1 , centroids.shape[0]):

        dist = np.linalg.norm(dataSetRow - centroids[i, :-1])

        if dist < minDist:

            minDist = dist

            label = centroids[i, -1]

    print ("minDist:", str(minDist))

    return label

 

 

 

# Function: Get Centroids

# -------------

# Returns k random centroids, each of dimension n.

def getCentroids(dataSet, k):

    # Each centroid is the geometric mean of the points that

    # have that centroid's label. Important: If a centroid is empty (no points have

    # that centroid's label) you should randomly re-initialize it.

    result = np.zeros((k, dataSet.shape[1]))

    for i in range(1, k + 1):

        oneCluster = dataSet[dataSet[:, -1] == i, :-1]

        result[i - 1, :-1] = np.mean(oneCluster, axis = 0)

        result[i - 1, -1] = i

 

    return result

 

 

x1 = np.array([1, 1])

x2 = np.array([2, 1])

x3 = np.array([4, 3])

x4 = np.array([5, 4])

testX = np.vstack((x1, x2, x3, x4))

 

result = kmeans(testX, 2, 10)

print ("final result:")

print (result)

运行结果：

iteration:

 0

dataSet:

 [[ 1.  1.  1.]

 [ 2.  1.  2.]

 [ 4.  3.  0.]

 [ 5.  4.  0.]]

centroids:

 [[ 1.  1.  1.]

 [ 2.  1.  2.]]

minDist: 0.0

minDist: 0.0

minDist: 2.82842712475

minDist: 4.24264068712

iteration:

 1

dataSet:

 [[ 1.  1.  1.]

 [ 2.  1.  2.]

 [ 4.  3.  2.]

 [ 5.  4.  2.]]

centroids:

 [[ 1.          1.          1.        ]

 [ 3.66666667  2.66666667  2.        ]]

minDist: 0.0

minDist: 1.0

minDist: 0.471404520791

minDist: 1.88561808316

iteration:

 2

dataSet:

 [[ 1.  1.  1.]

 [ 2.  1.  1.]

 [ 4.  3.  2.]

 [ 5.  4.  2.]]

centroids:

 [[ 1.5  1.   1. ]

 [ 4.5  3.5  2. ]]

minDist: 0.5

minDist: 0.5

minDist: 0.707106781187

minDist: 0.707106781187

final result:

[[ 1.  1.  1.]

 [ 2.  1.  1.]

 [ 4.  3.  2.]

 [ 5.  4.  2.]]

作业：实现对test_data中数据进行归类

层次聚类（上）-非监督学习，归类

算法描述：

假设有N个待聚类的样本，对于层次聚类来说，步骤： 
1、（初始化）把每个样本归为一类，计算每两个类之间的距离，也就是样本与样本之间的相似度；把每个样本看成一类，要计算距离需要提取特征向量，计算两两距离。1-2，1-3，1-4，1-5，2-3，2-4，2-5 
2、寻找各个类之间最近的两个类，把他们归为一类（这样类的总数就少了一个）；（从以上10个距离找出最近的，归为一类） 
3、重新计算新生成的这个类与各个旧类之间的相似度； 
4、重复2和3直到所有样本点都归为一类，结束

 

建立一棵树之后，我们可以根据阈值，来进行分类。假如距离小于某个值，那这棵树就分成两类了。

画下树的创建：

整个聚类过程其实是建立了一棵树，在建立的过程中，可以通过在第二步上设置一个阈值，当最近的两个类的距离大于这个阈值，则认为迭代可以终止。

那么类和类之间距离怎么计算呢？有以下三种方法

另外关键的一步就是第三步，如何判断两个类之间的相似度有不少种方法。这里介绍一下三种：

SingleLinkage：又叫做 nearest-neighbor ，就是取两个类中距离最近的两个样本的距离作为这两个集合的距离（在两个类之间，第一个类包括几个样本，第二个类包括几个样本，我们采用样本之间最近的距离作为两个类的距离），也就是说，最近两个样本之间的距离越小，这两个类之间的相似度就越大。容易造成一种叫做 Chaining 的效果，两个 cluster 明明从“大局”上离得比较远，但是由于其中个别的点距离比较近就被合并了，并且这样合并之后 Chaining 效应会进一步扩大，最后会得到比较松散的 cluster 。（这里有个缺陷就是用两个最近距离代表两个群之关系，有点松散。两个群可能存在整体比较远，只是有两个点近，这就比较松散了。）

 

CompleteLinkage：这个则完全是 Single Linkage 的反面极端，取两个集合中距离最远的两个点的距离作为两个集合的距离。其效果也是刚好相反的，限制非常大，两个 cluster 即使已经很接近了，但是只要有不配合的点存在，就顽固到底，老死不相合并，也是不太好的办法。这两种相似度的定义方法的共同问题就是指考虑了某个有特点的数据，而没有考虑类内数据的整体特点。

Average-linkage：这种方法就是把两个集合中的点两两的距离全部放在一起求一个平均值，相对也能得到合适一点的结果。（两个群求平均值，但均值会受距离大的影响）

Average-linkage的一个变种就是取两两距离的中值，与取均值相比更加能够解除个别偏离样本对结果的干扰。

层次聚类（下）

层次聚类代码：

from numpy import *

 

"""

Code for hierarchical clustering, modified from

Programming Collective Intelligence by Toby Segaran

(O'Reilly Media 2007, page 33).

"""

 

class cluster_node:

    def __init__(self,vec,left=None,right=None,distance=0.0,id=None,count=1):

        self.left=left

        self.right=right

        self.vec=vec

        self.id=id

        self.distance=distance

        self.count=count #only used for weighted average

 

def L2dist(v1,v2):

    return sqrt(sum((v1-v2)**2))

 

def L1dist(v1,v2):

    return sum(abs(v1-v2))

 

# def Chi2dist(v1,v2):

#     return sqrt(sum((v1-v2)**2))

 

def hcluster(features,distance=L2dist):

    #cluster the rows of the "features" matrix

    distances={}

    currentclustid=-1

 

    # clusters are initially just the individual rows

    clust=[cluster_node(array(features[i]),id=i) for i in range(len(features))]

 

    while len(clust)>1:

        lowestpair=(0,1)

        closest=distance(clust[0].vec,clust[1].vec)

 

        # loop through every pair looking for the smallest distance

        for i in range(len(clust)):

            for j in range(i+1,len(clust)):

                # distances is the cache of distance calculations

                if (clust[i].id,clust[j].id) not in distances:

                    distances[(clust[i].id,clust[j].id)]=distance(clust[i].vec,clust[j].vec)

 

                d=distances[(clust[i].id,clust[j].id)]

 

                if d

                    closest=d

                    lowestpair=(i,j)

 

        # calculate the average of the two clusters

        mergevec=[(clust[lowestpair[0]].vec[i]+clust[lowestpair[1]].vec[i])/2.0 \

            for i in range(len(clust[0].vec))]

 

        # create the new cluster

        newcluster=cluster_node(array(mergevec),left=clust[lowestpair[0]],

                             right=clust[lowestpair[1]],

                             distance=closest,id=currentclustid)

 

        # cluster ids that weren't in the original set are negative

        currentclustid-=1

        del clust[lowestpair[1]]

        del clust[lowestpair[0]]

        clust.append(newcluster)

 

    return clust[0]

 

 

def extract_clusters(clust,dist):

    # extract list of sub-tree clusters from hcluster tree with distance

    clusters = {}

    if clust.distance

        # we have found a cluster subtree

        return [clust]

    else:

        # check the right and left branches

        cl = []

        cr = []

        if clust.left!=None:

            cl = extract_clusters(clust.left,dist=dist)

        if clust.right!=None:

            cr = extract_clusters(clust.right,dist=dist)

        return cl+cr

 

def get_cluster_elements(clust):

    # return ids for elements in a cluster sub-tree

    if clust.id>=0:

        # positive id means that this is a leaf

        return [clust.id]

    else:

        # check the right and left branches

        cl = []

        cr = []

        if clust.left!=None:

            cl = get_cluster_elements(clust.left)

        if clust.right!=None:

            cr = get_cluster_elements(clust.right)

        return cl+cr

 

 

def printclust(clust,labels=None,n=0):

    # indent to make a hierarchy layout

    for i in range(n): print (' '),

    if clust.id<0:

        # negative id means that this is branch

        print ('-')

    else:

        # positive id means that this is an endpoint

        if labels==None: print (clust.id)

        else: print (labels[clust.id])

 

    # now print the right and left branches

    if clust.left!=None: printclust(clust.left,labels=labels,n=n+1)

    if clust.right!=None: printclust(clust.right,labels=labels,n=n+1)

 

 

 

def getheight(clust):

    # Is this an endpoint? Then the height is just 1

    if clust.left==None and clust.right==None: return 1

 

    # Otherwise the height is the same of the heights of

    # each branch

    return getheight(clust.left)+getheight(clust.right)

 

def getdepth(clust):

    # The distance of an endpoint is 0.0

    if clust.left==None and clust.right==None: return 0

 

    # The distance of a branch is the greater of its two sides

    # plus its own distance

    return max(getdepth(clust.left),getdepth(clust.right))+clust.distance

 

 

决策树算法 –监督学习 分类

0、机器学习中算法的评价

• 准确率
• 速度
• 强壮性（有些值缺失时）
• 可规模性
• 可解释性（运行结果与观察是否一致）

1、什么是决策树（decision tree）

决策树是一个类似于流程图的树结构：其中，每个内部结点表示在一个属性上的测试，每个分支代表一个属性输出，而每个树叶结点代表类或类分布。树的最顶层是根结点。

 

Outlook今天整个天气 overcast代表阴天，

Humidity 湿度，这是个连续值，要离散化，经常见到的是类别

2、它是机器学习中分类方法中一个重要的算法

3、构造决策树的基本算法

例子：以下是收集电商系统买电脑情况，“什么样的人买电脑”

下图为数据集： 第一列分年轻人，中年人，年老人，credit_rating信用：普通和优秀。我们可以根据下面数据，建立决策树，建立决策树的目的，当有新人，进来时，判断此人是否买电脑。是一个分类器，建好的模型。

下图为依据数据集建立的决策树：

年龄为根节点，当年龄为中年人，就买，不用区分，达到区分类别目的，当为年轻人时，有时候买，有时候不买，所以需要利用下一个属性student或信用度来衡量买不买 ，对照数据集进行解释。

4、熵（entropy）(如何创建决策树呢)

1948年，香农提出了 ”信息熵(entropy)“的概念。

一条信息的信息量大小和它的不确定性有直接的关系。

要搞清楚一件非常非常不确定的事情，或是我们一无所知的事情，需要了解大量信息。

信息量的度量就等于不确定性的多少。

example：猜世界杯冠军，假如一无所知，猜多少次？（二分法） 
每个队夺冠的几率不是相等的 
比特(bit)来衡量信息的多少（下面是32个足球队，如果想知道足球冠军是谁，可以用以下公式，如果概率都相等的话1/32,总值是5，也就是需要猜5次，如果了解更深的话，可能需要次数更少）

 

变量的不确定性越大，熵越大。上面的这个小例子中，当P=1/32时，熵最大，为5。

 

5、决策树归纳算法（ID3）

1970-1980， J.Ross. Quinlan, 提出ID3算法

优先选择信息获取量最大的属性作为属性判断结点（那么选哪个节点做为第一个节点呢，为什么是age为第一）

信息获取量(Information Gain)：Gain(A) = Info(D) - Infor_A(D)

（Gain A的信息量等于有D时信息量减去）

age属性信息获取量的计算过程如下所示：

 

 

 

 

同理，计算income，student，credit_rating的信息获取量(info(D)是不变，减去info come D)，因为age的信息获取量最大，所以首先将age属性作为节点来分枝（如下图），以此类推。Gain(income)=0.0.29 Gain(student)=o.151 G(credit_rating)=0.0.48

通过第一轮就变成如下图，其中中年人都是yes了。不用再分了。因为当年龄为年轻人时，标签有yes和no所以需要继续，进行分。当为年轻人时，要再次计算新的点为节点。

 

第二轮：gain(incom)=gain(D)-gain income(D)

算法步骤：

• 树以代表训练样本的单个结点开始。
• 如果样本都在同一个类，则该结点成为树叶，并用该类标号。（就像为中年人分类都为yes）
• 否则，算法使用称为信息增益的基于熵的度量作为启发信息(熵值大的成为顶层节点)，选择能够最好地将样本分类的属性。该属性成为该结点的“测试”或“判定”属性。在算法的该版本中。（否则继续分）
• 所有的属性都是分类的，即离散值。连续属性必须离散化（如果年龄是数字，要分成不同范围）。
• 对测试属性的每个已知的值，创建一个分枝，并据此划分样本。（根据属性的不同情况（年轻人，中年人，年老人）进行分支）
• 算法使用同样的过程，递归地形成每个划分上的样本判定树。一旦一个属性出现在一个结点上，就不在该结点的任何后代上考虑它。（一旦一个属性，成为一个节点，后续不在考虑它,age已经成为节点，后边不在考虑）
• 递归划分步骤仅当下列条件之一成立停止： 
  • (a) 给定结点的所有样本属于同一类。
  • (b) 没有剩余属性可以用来进一步划分样本。在此情况下，使用多数表决。这涉及将给定的结点转换成树叶，并用样本中的多数所在的类标记它。替换地，可以存放结点样本的类分布。

6、其他决策树算法

C4.5: Quinlan 
Classification and Regression Trees (CART): (L. Breiman, J. Friedman, R. Olshen, C. Stone) 
共同点：都是贪心算法，自上而下(Top-down approach) 
区别：属性选择度量方法不同： C4.5 （gain ratio), CART(gini index), ID3 (Information Gain)

7、如何处理连续性变量的属性

离散化（阈值的选择很关键）

8、决策树的优点

直观，便于理解，小规模数据集有效

9、决策树的缺点

处理连续变量不好 
类别较多时，错误增加的比较快 
可规模性一般

 

1、python

本课程的机器学习的算法都是基于Python语言实现的，所以你需要有一定的python语言基础，可以参考彭亮在麦子学院讲授的“Python语言编程基础”。

2、python机器学习的库：scikit-learn

特性： 
1）简单高效的数据挖掘和机器学习分析 
2）对所有用户开放，根据不同需求高度可重用性 
3）基于Numpy, SciPy和matplotlib 
4）开源，商用级别：获得 BSD许可

覆盖问题领域： 
分类（classification),，回归（regression)， 聚类（clustering)， 
降维(dimensionality reduction)，模型选择(model selection)， 预处理(preprocessing)

3、使用scikit-learn

方式一：pip, easy_install（两个都是python安装package的工具，感觉pip更好用） 
方式二（推荐）： 可使用Anaconda(这是一个科学计算环境 ，包含numpy, scipy，matplotlib等科学计算常用package，当然也包含scikit-learn包） 
anaconda下载地址：www.continuum.io/downloads 
anaconda安装注意问题：匹配的Python解释器版本（2.7 or 3.5）, 系统版本（32位or64位）

4、安装Graphviz（数据可视化软件）

下载地址：www.graphviz.org 
安装完成后，将C:\Program Files (x86)\Graphviz2.38\bin（找你的graphviz/bin的路径）加入到系统变量path中

 

5、决策树算法实现

5.1、将原始数据录入csv文件中（如下图）

 

5.2、引入sk-learn相关的package

 

5.3、读取csv文件的数据到程序中

 

5.3、对数据预处理

 

5.4、决策树分类的核心代码

 

5.5、生成dot文件（结果不够直观）

 

dot文件： 

5.6、将dot文件用graphviz转换为pdf文件

在命令行下，cd到你的dot文件的路径下，输入 
dot -Tpdf filename.dot -o output.pdf 
（filename以dot文件名为准） 
可以看见同路径下生成了一个pdf文件

如图： 

5.7、测试代码

 

5.8、源程序

#coding=gbk

 

# DictVectorizer:数据类型转换

from sklearn.feature_extraction import DictVectorizer

 

# csv:原始数据放在csv文件中，该package为python自带，不需要安装

import csv

 

#引入数据预处理包、决策树包、读写字符串包

from sklearn import preprocessing

from sklearn import tree

from sklearn.externals.six import StringIO

 

 

#从csv文件中读取数据，并保存到allElectronicsData变量中

allElectronicsData = open(r'D:\eclipse\mars\project\DeepLearningBasicsMachineLearning\Datasets\AllElectronics.csv','r')

# csv的reader方法按行读取数据

reader = csv.reader(allElectronicsData)

#next方法读取到csv文件的第一行数据

headers = next(reader)

#打印第一行数据

print(headers)

 

 

#建两个list，featureList装特征值，labelList装类别标签

featureList = []

labelList = []

 

#遍历csv文件的每一行

for row in reader:

    #将类别标签加入到labelList中

    labelList.append(row[len(row)-1])

    #下面这几步的目的是为了让特征值转化成一种字典的形式，就可以调用sk-learn里面的DictVectorizer，直接将特征的类别值转化成0,1值

    rowDict = {}

    for i in range(1,len(row)-1):

        rowDict[headers[i]] = row[i]

    featureList.append(rowDict)

print(featureList)

 

#实例化    

vec = DictVectorizer()

dummyX = vec.fit_transform(featureList).toarray()

print("dummyX:"+str(dummyX))

print(vec.get_feature_names())

 

# label的转化，直接用preprocessing的LabelBinarizer方法

lb = preprocessing.LabelBinarizer()

dummyY = lb.fit_transform(labelList)

print("dummyY:"+str(dummyY))

print("labelList:"+str(labelList))

 

 

#criterion是选择决策树节点的标准，这里是按照“熵”为标准，即ID3算法；默认标准是gini index，即CART算法。

clf = tree.DecisionTreeClassifier(criterion = 'entropy')

clf = clf.fit(dummyX,dummyY)

print("clf:"+str(clf))

 

#生成dot文件

with open("allElectronicInformationGainOri.dot",'w') as f:

    f = tree.export_graphviz(clf,feature_names = vec.get_feature_names(),out_file = f)

 

#测试代码，取第1个实例数据，将001->100，即age：youth->middle_aged    

oneRowX = dummyX[0,:]

print("oneRowX:"+str(oneRowX))

newRowX = oneRowX

newRowX[0] = 1

newRowX[2] = 0

print("newRowX:"+str(newRowX))

 

#预测代码

predictedY = clf.predict(newRowX)

print("predictedY:"+str(predictedY))

5.9、sk-learn的决策树文档

地址：scikit-learn.org/stable/modules/tree.html

 

 

 

 

 

神经网络算法-分类算法

1. 背景

1.1 以人脑中的神经网络为启发，历史上出现过很多不同版本 
1.2 最著名的算法是1980年的 backpropagation算法

2. 多层向前神经网络(Multilayer Feed-Forward Neural Network)：今天介绍一种重要神经网络

2.1 Backpropagation算法被使用在多层前馈神经网络上 

什么是多层向前神经网络呢？了解概念
2.2 多层向前神经网络由以下部分组成（如下图）：所谓多层，有多层，输入层，隐藏层 
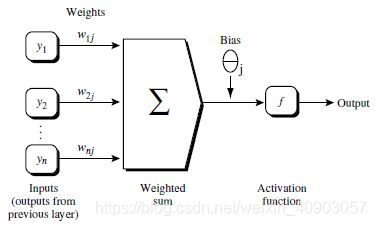
输入层(input layer), 隐藏层 (hidden layer), 输出层 (output layer)

 

2.3 每层由单元(unit)组成 
2.4 输入层(input layer)是由训练集的实例特征向量传入 。
2.5 经过连接结点的权重(weight)传入下一层，一层的输出是下一层的输入 
2.6 隐藏层的个数可以是任意多层的，输入层只有一层，输出层只有一层 
2.7 根据生物学来源定义，每个单元(unit)也可以被称作神经结点（根据人脑） 
2.8 以上称为2层的神经网络（输入层不算） 
2.9 一层中每个节点加权求和，然后根据非线性方程转化为输出 
2.10 作为多层向前神经网络，理论上，因为输出是非线性方程，所以如果有足够多的隐藏层(hidden layer) 和足够大的训练集, 可以模拟出任何方程

3. 设计神经网络结构（多少个隐藏层及单元个数，输入层有多少个单元，输出层有多少个单元）

3.1 使用神经网络训练数据之前，必须确定神经网络的层数，以及每层单元的个数

3.2 特征向量在被传入输入层时通常被先标准化(normalize）到0和1之间 （为了加速学习过程）

3.3 离散型变量可以被编码成每一个输入单元对应一个特征值可能赋的值。 
比如：特征值A可能取三个值（a0, a1, a2), 可以使用3个输入单元来代表A。 
如果A=a0, 那么代表a0的单元值就取1, 其他取0； 
如果A=a1, 那么代表a1de单元值就取1，其他取0，以此类推

3.4 神经网络即可以用来做分类(classification）问题，也可以解决回归(regression)问题 
对于分类问题，如果是2类，可以用一个输出单元表示（0和1分别代表2类），如果多于2类，每一个类别用一个输出单元表示，所以输出层的单元数量通常等于类别的数量

3.5 没有明确的规则来设计最好有多少个隐藏层，根据实验测试和误差，以及准确度来实验并改进（根据实验结果和误差，来确定隐层个数，如果不准确，添加隐层）

4. 交叉验证方法(Cross-Validation)（算准确度）

总体思想：把整个数据分成10份。第一份用于验证，其它9份用于训练算法。看看准确度。让第二份数当测试集，其它份数据当训练集，看看准确度。依次类推，然后，把所有值求平均值。

 

“k-fold cross-validation”：k份交叉验证方法

5.Backpropagation算法

5.1 通过迭代性来处理训练集中的实例 （每次一条数据）
5.2 对比经过神经网络后，输出层预测值(predicted value)与真实值(target value)之间差值 （每条数据经过网络层，会得到一个预测值，通过对比预测值和真实值，就能知道误差）
5.3 反方向（从输出层=>隐藏层=>输入层）来以最小化误差(error)来更新每个连接的权重(weight) （按照一定算法，通过反向更新权重来减少误差）
5.4 算法详细介绍 
输入：D：数据集，l 学习率(learning rate)（这个在反方向更新用得到，用于确定学习速度）， 一个多层前馈神经网络 
输出：一个训练好的神经网络(a trained neural network)-所谓训练好的神经网络指的是已经权重已经最优化了。可以直接用于项目中了。

5.4.1 初始化权重(weights)和偏向(bias): 随机初始化在-1到1之间，或者-0.5到0.5之间，每个单元有一个偏向

5.4.2 对于每一个训练实例X，执行以下步骤：

    5.4.2.1： 由输入层向前传送、

（这个方程中：Ij 表示某个输出单元，wij表示权重，Qi表示输入层某个单元，0j表示偏向）下面这个图能更形象:f表示激活函数（非线性sigmoid,tanh-双曲正切）

 

5.4.2.2 根据误差(error)反向传送

 

求输层误差

求隐藏层误差

求误差的目的就是更新权重，更新权重目的找到误差最小。在数学里，采用计算微积分实现的。（l）指的学习率，相当于在找最小值时步长值。是0-1的一个值。

隐藏层误差，反向时Errk指隐藏层上一层误差 wjk指权重

权重更新量=学习率*终点误差*起始点输出值

偏向更新量=学习率*当前节点误差

 

5.4.3 终止条件（我们通过训练集进行训练，什么时修改停止呢）

    5.4.3.1 权重的更新低于某个阈值（当权重更新已经达到很小时，表示已经找到最小值了）

    5.4.3.2 预测的错误率低于某个阈值（当预测准确率达到某个值，如百分之3）

    5.4.3.3 达到预设一定的循环次数

6. Backpropagation 算法举例