《Python编程:从入门到实践》第15章-生成数据 习题
开心~开始学习数据可视化啦
文章目录
- 15-1 立方
- 15-2 彩色立方
- 15-3 分子运动
- 15-4 改进的随机漫步
- 15-5 重构
- 15-6 自动生成标签
- 15-7 两个D8骰子
- 15-8 同时掷三个骰子
- 15-9 将点数相乘
- 15-10 练习使用本章介绍的两个库
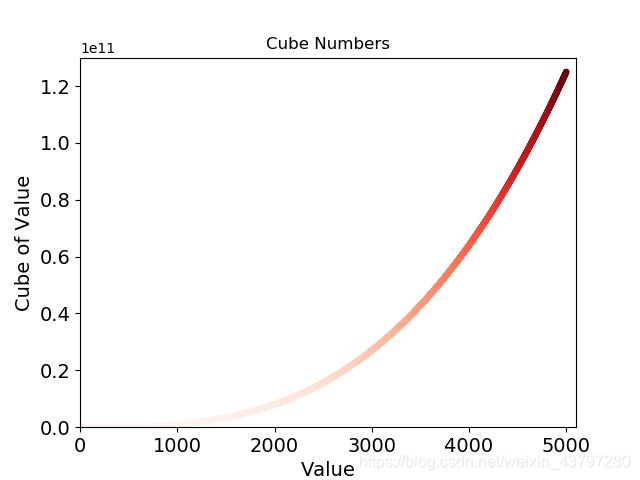
15-1 立方
数字的三次方被称为其立方。请绘制一个图形,显示前5个整数的立方值,再绘制一个图形,显示前5000个整数的立方值。
import matplotlib.pyplot as plt
#创建1-5000的整数列表
x_values = list(range(1,5001))
y_values = [x**3 for x in x_values]
plt.scatter(x_values, y_values, edgecolor='none', s=20)
#设置图标标题并给坐标轴指定标签
plt.title("Cube Numbers")
plt.xlabel("Value", fontsize=24)
plt.ylabel("Cube of Value", fontsize=14)
#设置刻度标记的大小
plt.tick_params(axis='both', which='major', labelsize=14)
plt.show()
15-2 彩色立方
给你前面绘制的立方图指定颜色映射
import matplotlib.pyplot as plt
#创建1-5000的整数列表
x_values = list(range(1,5001))
y_values = [x**3 for x in x_values]
plt.scatter(x_values, y_values, c=y_values, cmap=plt.cm.Reds, edgecolor='none', s=20)
#设置图标标题并给坐标轴指定标签
-snip
#设置刻度标记的大小
-snip-
#设置每个坐标轴的取值范围
-snip-
plt.show()
这里尝试了一下cmap=plt.cm.Reds 红色的颜色映射
build
15-3 分子运动
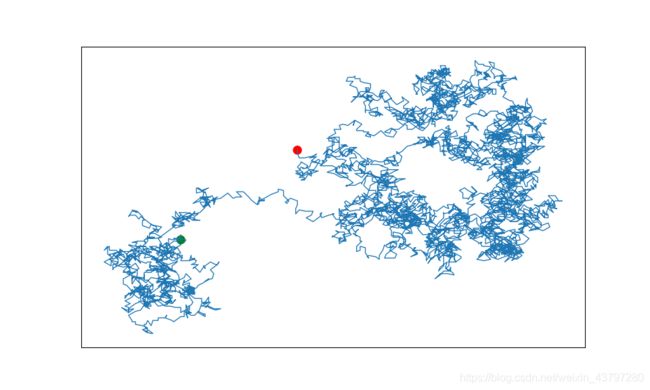
修改rw_visual.py,将其中的plt.scatter()替换为plt.plot()。为模拟花粉在水滴表面的运动路径,向plt.plot()传递rw.x_values和rw.y_values,并指定实参值linewidth。使用5000个点而不是50000个点。
import matplotlib.pyplot as plt
from random_walk import RandomWalk
# 只要程序处于活动状态,就不断地模拟随机漫步
while True:
#创建一个RandomWalk实例,并将其包含的点都绘制出来。
#使用5000个点
rw = RandomWalk()
rw.fill_walk()
#设置绘图窗口的尺寸
plt.figure(dpi=96, figsize=(10,6))
# 用plt.plot()来模拟花粉在水滴表面的运动路径。
# 设置绘制线条的粗细。
plt.plot(rw.x_values, rw.y_values, linewidth=1)
plt.scatter(0, 0, c='green', edgecolor='none', s=100)
plt.scatter(rw.x_values[-1], rw.y_values[-1], c='red', edgecolor='none', s=100)
# 隐藏坐标轴
plt.axes().get_xaxis().set_visible(False)
plt.axes().get_yaxis().set_visible(False)
plt.show()
keep_running = input("Make another walk? (y/n): ")
if keep_running == 'n':
break
Line17为主要变化的代码
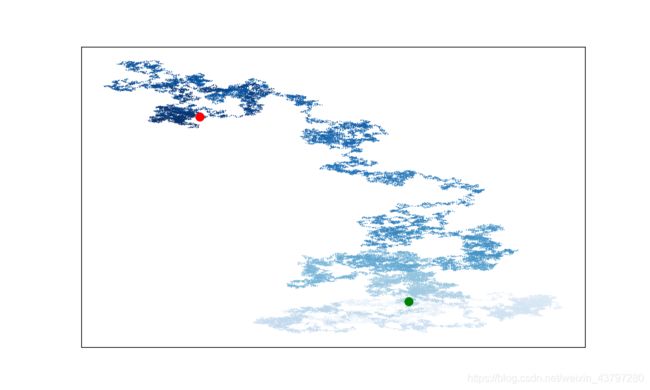
15-4 改进的随机漫步
在类RandomWalk中,x_step和y_step是根据相同的条件生成的:从列表[-1, 1]中随机地选择方向,并从列表[0, 1, 2, 3, 4]中随机地选择距离。请修改这些列表中的值,看看对随机漫步路径有何影响。尝试使用更长的距离选择列表,如0~8;或者将-1从 x 或 y 方向列表中删除。
(1)使用更长的距离选择列表:
from random import choice
class RandomWalk():
"""一个生成随机漫步数据的类"""
def __init__(self, num_points=5000):
"""初始化随机漫步的属性"""
self.num_points = num_points
#所有随机漫步都始于(0, 0)
self.x_values = [0]
self.y_values = [0]
def fill_walk(self):
"""计算随机漫步包含的所有点"""
# 不断漫步,直到列表达到指定的长度
while len(self.x_values) < self.num_points:
# 决定前进方向以及沿这个方向前进的距离
x_direction = choice([1, -1])
x_distance = choice([0, 1, 2, 3, 4, 5, 6, 7, 8])
x_step = x_direction * x_distance
y_direction = choice([1,-1])
y_distance = choice([0, 1, 2, 3, 4, 5, 6, 7, 8])
y_step = y_direction * y_distance
# 拒绝原地踏步
if x_step == 0 and y_step == 0:
continue
# 计算下一个点的x值和y值
next_x = self.x_values[-1] + x_step
next_y = self.y_values[-1] + y_step
self.x_values.append(next_x)
self.y_values.append(next_y)
15-5 重构
方法fill_walk()很长。请新建一个名为get_step()的方法,用于确定每次漫步的距离和方向,并计算这次漫步将如何移动。然后,在fill_walk()中调用get_step()两次:
x_step = self.get_step()
y_step = self.get_step()
通过这样的重构,可缩小fill_walk()的规模,让这个方法阅读和理解起来更容易。
from random import choice
class RandomWalk():
"""一个生成随机漫步数据的类"""
def __init__(self, num_points=5000):
"""初始化随机漫步的属性"""
self.num_points = num_points
#所有随机漫步都始于(0, 0)
self.x_values = [0]
self.y_values = [0]
def get_step(self):
"""确定每次漫步的距离和方向,并计算这次漫步将如何移动"""
# 决定前进方向以及沿这个方向前进的距离
x_direction = choice([1, -1])
x_distance = choice([0, 1, 2, 3, 4])
x_step = x_direction * x_distance
y_direction = choice([1, -1])
y_distance = choice([0, 1, 2, 3, 4])
y_step = y_direction * y_distance
return x_step
return y_step
def fill_walk(self):
"""计算随机漫步包含的所有点"""
# 不断漫步,直到列表达到指定的长度
while len(self.x_values) < self.num_points:
x_step = self.get_step()
y_step = self.get_step()
# 拒绝原地踏步
if x_step == 0 and y_step == 0:
continue
# 计算下一个点的x值和y值
next_x = self.x_values[-1] + x_step
next_y = self.y_values[-1] + y_step
self.x_values.append(next_x)
self.y_values.append(next_y)
重构函数:line14 - line26
15-6 自动生成标签
请修改die.py和 dice_visual.py die_visual.py ,将用来设置hist.x_labels值的列表替换为一个自动生成这种列表的循环。如果你熟悉列表解析,可尝试将die_visual.py和dice_visual.py中其他for循环也替换为列表解析。
[注:这里有个modification—This should say to modify die_visual.py, not die.py. This will be corrected in future printings.]
from die_1 import Die
import pygal
# 创建一个D6
die = Die()
# 掷几次骰子,并将结果存储在一个列表中
results = [die.roll() for roll_num in range(1000)]
# 分析结果
frequencies = [results.count(value) for value in range(1, die.num_sides+1)]
#对结果进行可视化
hist = pygal.Bar()
hist.title = "Results of rolling one D6 1000 times."
hist.x_labels = [str(value) for value in range(1, die.num_sides+1)]
hist.x_title = "Result"
hist.y_title = "Frequency of Result"
hist.add('D6', frequencies)
hist.render_to_file('die_visual.svg')
列表解析
将for循环和创建新元素的代码合并成一行,并自动附加新元素。
Line 8, 11, 17为列表解析的代码。
一般语句为:
列表名 = [a的函数 for a in range()]
这点要理解一下。能写出来。
可视化如下
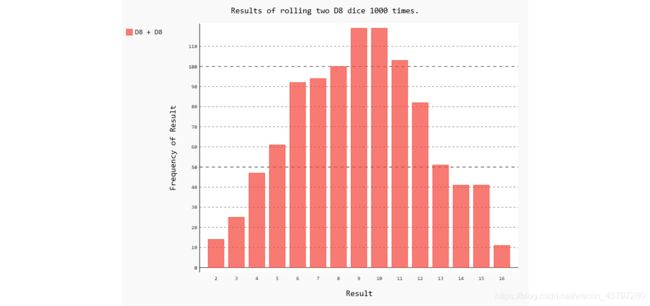
15-7 两个D8骰子
请模拟同时掷两个8面骰子1000次的结果。逐渐增加掷骰子的次数,直到系统不堪重负为止。
import pygal
from die_1 import Die
# 创建两个D8骰子
die_1 = Die(8)
die_2 = Die(8)
# 掷骰子多次,并将结果存储到一个列表中
results = []
for roll_num in range(1000):
result = die_1.roll() + die_2.roll()
results.append(result)
# 分析结果
frequencies = []
max_result = die_1.num_sides + die_2.num_sides
for value in range(2, max_result+1):
frequency = results.count(value)
frequencies.append(frequency)
# 可视化结果
hist = pygal.Bar()
hist.title = "Results of rolling two D8 dice 1000 times."
hist.x_labels = [str(value) for value in range(2, max_result+1)]
hist.x_title = "Result"
hist.y_title = "Frequency of Result"
hist.add('D8 + D8', frequencies)
hist.render_to_file('dice_visual_2.svg')
如何修改
主要是给Die类传递实参8。
修改标题,修改标签。
系统不堪重负
大概次数增加到1000万次后,时间达到30s左右。
一亿次时,感觉PC要炸。
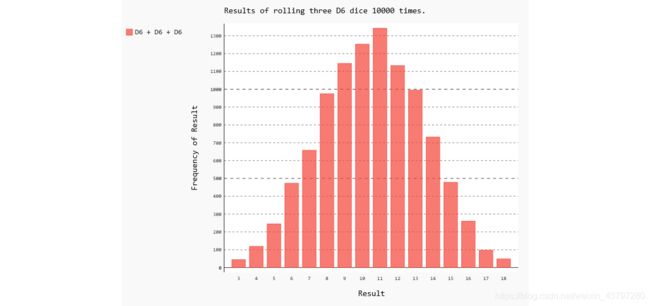
15-8 同时掷三个骰子
如果你同时掷三个D6骰子,可能得到的最小点数为3,而最大点数为18。请通过可视化展示同时掷三个D6骰子的结果。
import pygal
from die_1 import Die
# 创建三个D6骰子
die_1 = Die()
die_2 = Die()
die_3 = Die()
# 掷骰子多次,并将结果存储到一个列表中
results = []
for roll_num in range(10000):
result = die_1.roll() + die_2.roll() + die_3.roll()
results.append(result)
# 分析结果
frequencies = []
max_result = die_1.num_sides + die_2.num_sides + die_3.num_sides
for value in range(3, max_result+1):
frequency = results.count(value)
frequencies.append(frequency)
# 可视化结果
hist = pygal.Bar()
hist.title = "Results of rolling three D6 dice 10000 times."
hist.x_labels = [str(value) for value in range(3, max_result+1)]
hist.x_title = "Result"
hist.y_title = "Frequency of Result"
hist.add('D6 + D6 + D6', frequencies)
hist.render_to_file('dice_visual_3.svg')
①多创建一个Die()实例。(因为默认值为)
②修改标题,标签。
③将最小和修改为3。
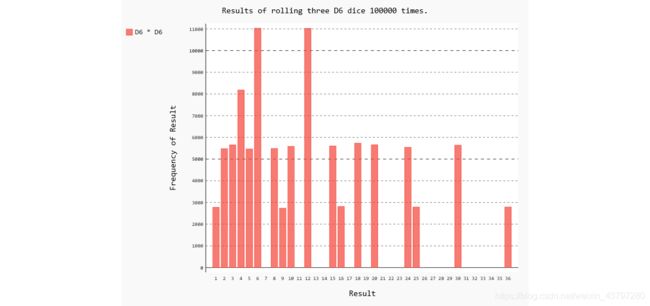
15-9 将点数相乘
同时掷两个骰子时,通常将它们的点数相加。请通过可视化展示将两个骰子的点数相乘的结果。
import pygal
from die_1 import Die
# 创建2个D6骰子
die_1 = Die()
die_2 = Die()
# 掷骰子多次,并将结果存储到一个列表中
results = []
for roll_num in range(100000):
result = die_1.roll() * die_2.roll()
results.append(result)
# 分析结果
frequencies = []
max_result = die_1.num_sides * die_2.num_sides
for value in range(1, max_result+1):
frequency = results.count(value)
frequencies.append(frequency)
# 可视化结果
hist = pygal.Bar()
hist.title = "Results of rolling three D6 dice 100000 times."
hist.x_labels = [str(value) for value in range(1,max_result+1)]
hist.x_title = "Result"
hist.y_title = "Frequency of Result"
hist.add('D6 * D6', frequencies)
hist.render_to_file('dice_visual_4.svg')
15-10 练习使用本章介绍的两个库
尝试使用matplotlib通过可视化来模拟掷骰子的情况,并尝试使用Pygal通过可视化来模拟随机漫步的情况。