提高图形匹配精度，亮风台提出「完全可训练」的图匹配方法｜CVPR 2020 Oral

来源｜亮风台投稿

6月14日-19日，CVPR 2020在线上举行，据了解，本届大会共收到6656篇投稿，接收论文1470篇，录用率约22%，低于CVPR 2019论文录用率（25%），为十年以来最低录用率。

在今年的CVPR上，AR公司亮风台提出完全可训练的图匹配方法，论文《Learning Combinatorial Solver for Graph Matching》入选CVPR 2020 Oral presentation（约5%比例）。据了解，在CVPR 2019上，亮风台投影AR新算法同样入选 Oral环节，该成果为投影AR技术应用落地提供了重要的技术基础。

在计算机视觉领域，基于学习的图匹配方法已经有十多年的发展和探索史，近几年发展和普及速度更迅速。然而，以往的基于学习的算法，无论有无深度学习策略，都主要集中在节点学习和/或边缘仿射的生成上，而对组合求解器的学习关注较少。

亮风台及其合作伙伴提出了一个完全可训练的图匹配框架，在该框架中，仿射学习和组合优化求解并不像以往的许多技术那样被明确地分开。团队首先将两个输入图之间建立节点对应的问题转化为从一个已构造的分配图中选择可靠节点的问题。随后，采用图网络块模块对图进行计算，形成各节点的结构化表示。最后为每个节点预测一个用于节点分类的标签，并在排列差分和一对一匹配约束的正则化下进行训练。

为了进行评估，新算法在四个公共基准上进行了测试，与包括非学习和基于学习的算法在内的八个最新基准进行了比较。该算法对噪声和异常值具有较强的鲁棒性，总体上优于所有的基线算法。

总体来说，新成果提出的图匹配学习框架有三个方面的贡献：

• 通过构造一个给定两个待匹配输入图的赋值图，将图匹配学习转化为节点选择学习；

• 将仿射学习和组合优化求解结合到一个统一的学习框架中，并扩展了用于结构表示和关系推理的图形网络块模块；

• 设计了一个新的损失函数，其中施加一对一匹配约束来监督网络的训练。

这些实验的源代码链接在论文中可以找到，原文链接：

http://openaccess.thecvf.com/content_CVPR_2020/html/Wang_Learning_Combinatorial_Solver_for_Graph_Matching_CVPR_2020_paper.html

代码链接：

新算法介绍：

1. 基于学习的图匹配

传统图匹配的研究主要依赖于手工构建的仿射关系，这些仿射关系作为组合求解器的输入。这种预先定义的参数关联模型会限制捕捉真实匹配任务结构的灵活性，不合适的关联模型可能会使匹配求解器偏离真实匹配解。

针对这一问题，图匹配的学习在提高匹配精度方面显示了其优越的性能，这主要是通过学习图亲和力度量的参数来代替手工构建的亲和力度量来提高的。大多数传统的学习图匹配算法都是有监督的算法，需要对每个正图中的每个节点对应关系进行详细的标记以进行训练。这些算法分别使用大余量方法、非线性逆优化和基于平滑的技术以有监督的方式训练匹配参数。与有监督方法相比，无监督方法不需要大量的节点级标记。后来，Leordeanu等人为二阶以上约束模型提供一个半监督学习公式。与这些方法不同，Cho提出为类的所有实例参数化一个图模型，并学习其结构属性以进行可视化对象匹配。

尽管深度学习技术在许多领域都显示出强大的威力，但关于图形匹配的深度学习的文献仍然有限。为数不多的开创性研究主要是对深网络中的参数亲合函数进行编码，以便在计算出的节点和边缘亲合下获得正确的匹配分配。Zanfir和Sminchisescu将图匹配作为一个二次指派问题，在使用深参数特征层次表示的一元和成对节点仿射下进行。它采用谱匹配作为组合求解器，对反向传播具有可微性。Wang等人使用图卷积网络（GCN）框架作为节点嵌入模块，该模块聚合图结构信息以生成节点音调相似性。通过这种方法，图匹配被放松为线性分配，并采用Sinkhorn网作为组合求解器。

我们的工作属于深度学习算法组。与以往的方法相比，我们的方法不仅关注于亲和函数的学习，而且关注于组合求解器的学习，它们被有效地组合成一个完全可训练的图网络。为了提高匹配精度，我们在学习框架中引入了强结构表示和它们之间的关系归纳偏差，并通过实验验证了其良好的性能。

2. 问题描述

2.1图匹配问题

n个节点的无向图可以用 表示，其中 和 分别表示节点集和边缘集。图通常由一个对称邻接矩阵 表示，当且仅当 与 之间存在边时， 。通常将非负实值权重 与所有节点对相关联，将邻接矩阵泛化为加权图。这种概括对于许多应用程序捕获节点之间的结构关系很重要。在本文的其余部分中，除非另有说明，否则所有提及的邻接矩阵均以实数值加权。

对于图匹配问题，给定两个节点为 的图 ，不失一般性我们假设 。图匹配问题可以表示为找到一个节点对应关系 以支持如下的全局一致性：

其中 表示 中第 个节点与 中第 个节点的一致性， 表示 中边 与 中边 的一致性。匹配矩阵 代表了匹配结果，即当且仅当 中第 个节点匹配 中第 个节点时 。在实际应用中，经常将图匹配约束为一一匹配，即 且 ，其中 表示n个元素为1的列向量。

令 表示图 的邻接矩阵，用于加权图匹配[1,18]的更常用公式定义为

其中 是节点间的不相似矩阵， 为平衡节点一致性与边一致性的权值， 表示矩阵的Frobenius范数。

上式表示的加权图匹配在实践中通常受到限制，因为每个图的边仅与标量属性相关联，并且边缘一致性函数仅限于边缘权重之差。在最近的研究中[6,7,9,11,19]，图匹配问题通常描述为

，

其中 是匹配矩阵X的向量化形式， 是图匹配亲密矩阵，定义为

其中 是将节点对应关系映射到整数索引的双射函数。

在本文中，我们主要研究上式的图匹配算法，因为它不仅可以编码边权重之差，而且还可以编码许多复杂的兼容性函数。

2.2 匹配作为节点标注问题

基本上，通过如下构造分配图 ，两个图 与 之间的图匹配问题可以解释为分配图上的节点标注问题。

给定成对的亲密矩阵K，我们通过将每个潜在的匹配关系 视为一个节点 ， 每个矩阵元素 对应于一条边 且其属性为 。图1为一个由亲密矩阵K构造的分配图示例，其中 与 之间每个候选匹配对应于分配图 中的一个节点。因此， 与 之间的原始图匹配问题等同于选择图 中的可靠节点。

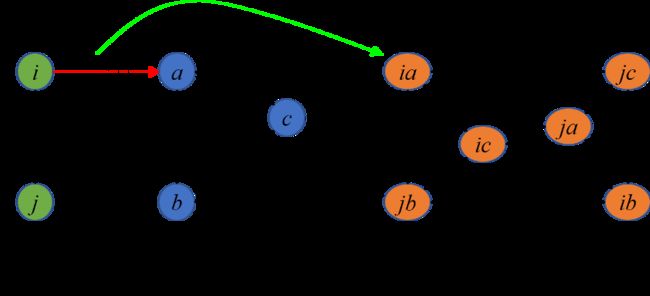
图1. 分配图构造示例

在过去的几十年中，针对上述图节点选择问题已经提出了许多算法。最近的一些研究包括使用特征向量技术在分配图中找到主要的强连通簇，以及采用Markov随机游走的统计数据来选择可靠的节点。

与这些手工设计的算法不同，本文提出了一种数据驱动的方法，该方法能够学习如何解决整数二次程序（IQP）问题。

3．我们的方法：群组敏感的图网络框架

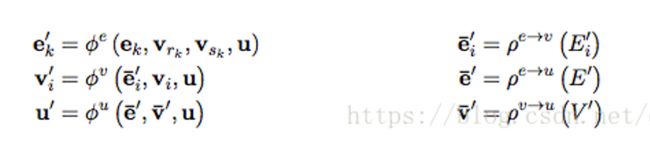
Battaglia等提出了一种图网络（GN）框架，该框架在图结构上运行并相应地构造其计算，定义了一类用于图结构表示的关系推理的函数。

GN框架中的主要计算单元是GN块，它是一个图到图的模块，该模块将图作为输入，对结构进行计算，然后将图作为输出返回。在GN块中处理的信息分为三个级别：实体由图的节点表示，实体的关系由边表示，系统级别的属性由全局属性表示。一个GN块包含：

三个聚合函数将输入图的信息从边到节点，最后到全局属性进行聚合；三个更新函数，使用聚合的信息来更新输出图。

原始图匹配问题的一对一匹配约束意味着：分配图 中与 （或 ）中的同一节点相关联的任何节点子集都包含一个且只有一个正节点。这些一对一匹配约束通常在指导解决图匹配问题中起关键作用。为了在我们的图网络中施加一对一的匹配约束，因此我们需要聚集分配图中的不同节点子集的信息。但是，中提出的GN框架由于缺乏群组级属性而不足以对节点的子集进行建模。

为解决上述问题，我们为图匹配问题开发了一个可感知群组属性的GN框架。我们的群组敏感的GN框架分为四个级别：实体由图形的节点表示，实体的关系由边表示，节点的子集属性由群组属性表示，系统级别的属性由全局属性表示。相应地，它包含5个聚合函数 ，和4个更新函数 ，

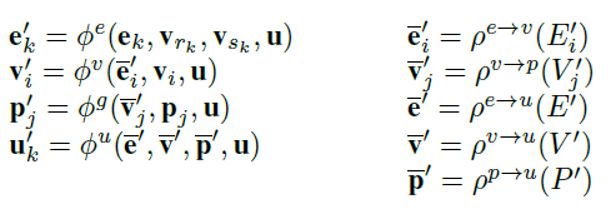
其中更新函数 和聚合函数 是从原始GN框架而来的，而更新函数 和聚合函数 是在我们群组敏感的GN模块中新提出的。

当将图G作为输入提供给群组敏感的GN块时，计算将从边、节点、群组、最后到全局级别进行。算法1显示了完整的群组敏感的GN块中的计算步骤。请注意，尽管我们在此假设了此步骤顺序，但实际计算并不一定需要按该顺序严格执行。同样，某些计算步骤可以根据不同的任务跳过。例如，在我们的图匹配实验中，全局属性是不必要的，因此将跳过步骤6、7、8和9。特别是，如果我们在某些任务中不使用群组级别的属性，并删除步骤4、5和8，则群组敏感的GN块简化为原始GN块。

4．实验

4.1 模拟2D点集

为了在更现实的场景中评估算法，我们遵循**[9]中的实验协议**生成2D点集，并寻找它们之间的对应关系。对于每个试验，我们构造两个集合 和 ，其中包含 个内部点，然后将 个离群点添加到这两个集合中。在平面的给定区域中随机选择 中的内点。然后，我们对齐添加高斯白噪声 干扰，然后旋转和平移整个点集，从而获得 中的对应内点。每组的离群点是从与内点相同的区域中随机选择。 中点坐标的范围是 。给定两对点 和 ，其边的亲密度计算为

其中 （及 ）表示点i和j（及a和b）之间的欧几里得距离，参数d控制亲密度对变形的敏感性。在整个实验中，我们将d设置为5。

我们分别通过改变离群点数目 （图2（a））和噪声参数 （图2（b））比较两种不同设置下算法的性能。

4.2 CMU House数据集

CMU房屋数据集包括111个图像序列帧，其中所有序列都包含经过变换的相同房屋对象。为了评估匹配精度，在所有帧中手动跟踪并标记了30个标定点。

对于训练中的每个试验，我们通过从111帧中随机选择两个示例来形成图像对。为了评估噪声对图匹配算法的影响，我们使用节点设置（n1, n2）=（10, 30），其中该对的第一个示例从30个标定点中随机选择10个点，这意味着第二个示例包含20个离群点。我们将每个标定点建模为一个图节点，然后通过Delaunay三角剖分建立图的边。每条边(i, j)赋予权重A~ij~，权重A~ij~计算为连接节点v~i~和v~j~之间的欧式距离。节点亲密度设置为0，并且计算 中的边(i,j)和 中的边(a,b)之间的边亲和度为

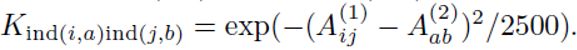
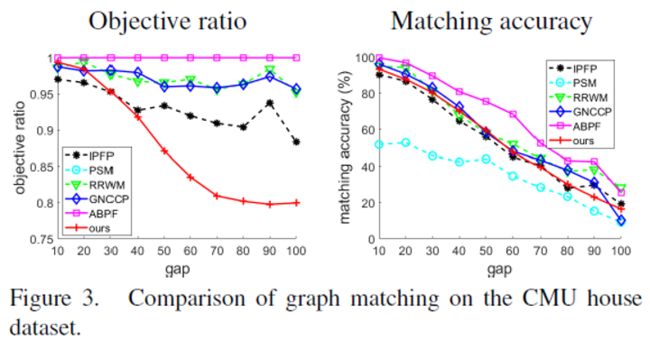
为了进行测试，我们匹配了所有可能的图像对，总共560对图像相隔10、20，...，100帧，其中增加的采样间隔意味着变形程度的增加。节点选择、图形构造和亲和力生成与训练时相同。图3示出了相对于不同图像序列间隔的性能曲线。

4.3 Willow数据集

此数据集由Minsu Cho等人提供，他们从Caltech-256和Pascal VOC 2007收集了五类图像，即汽车，鸭，人脸，摩托车和酒瓶。每个类至少包含40张具有不同实例的图像，并在每个类别的所有图像上手动绘制了10标定点标记在目标对象上。

我们使用Hessian检测器[13]提取兴趣点，并使用SIFT描述符[12]表示节点属性。通过节点的外观相似度来计算节点相似度。我们使用Delaunay三角剖分来构建图形边缘，并将每条边(i, j)与两个特征d~ij~和 关联，其中d~ij~是节点v~i~和v~j~之间的欧氏距离，而 是边(i,j) 与水平线之间的绝对角度，即 。随后，计算 中的边(i,j)和 中的边(a,b)之间的边亲和度为

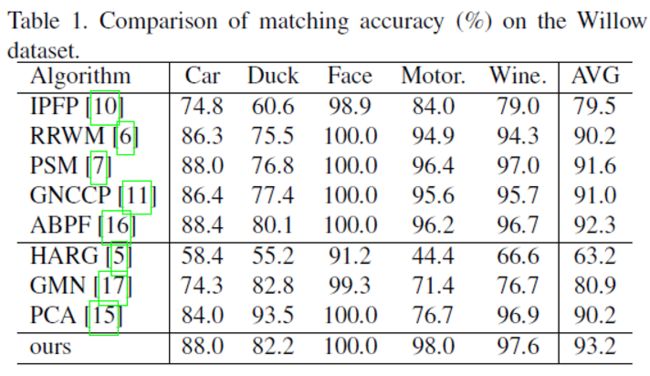
表1显示了我们的算法与基准算法的匹配精度（[5、15、17]的结果引自[15]）。

5. 结论

为了提高匹配精度，提出了一种新的图形匹配深度学习算法。我们首先将输入图之间建立节点对应的问题转化为从构造的指派图中选择可靠节点的问题。为了解决节点分类问题，我们提出了一种完全可训练的网络，该网络嵌入图网络块模块，通过对每个节点的邻域进行卷积，形成其结构化表示。此外，还提出了一种新的损失函数来编码一对一的匹配约束，以指导网络的训练。实验结果表明，我们的图匹配算法对噪声和离群点具有较强的鲁棒性，并优于目前最先进的算法。

觉得有用麻烦给个在看啦~