仿射变换（affine transformation）

官方教程

原理

1. 对原图像的物理坐标进行变换、旋转、比例等操作，从而得到目标图像。
2. 两幅图像之间的关系可以用一个 2 × 3 的矩阵表示：
   $$A=\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right]B=\left[\begin{array}{c}{b}_{11}\\ b_{21}\end{array}\right]$$

那么:$$M=\left[\begin{array}{ccc}{a}_{11}& a_{12}& b_{11}\\ a_{21}& a_{22}& b_{21}\end{array}\right]$$

假如使用A、B转换一个图像$X=\left[\begin{array}{c}x\\ y\end{array}\right]$： 目标图像：$T=A$*$\left[\begin{array}{c}x\\ y\end{array}\right]+B$ ，或者直接等于：$$M\ast \left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{c}{a}_{11}x+a_{12}y+b_{11}\\ a_{21}x+a_{22}y+b_{21}\end{array}\right]$$

3. 假如我们已知原图$X$和仿射矩阵$M$，则目标图像为：$T=M\ast X$。但是如何得到仿射矩阵，可由原图中三个点和目标图中三个点，他们的对应关系就是仿射矩阵。

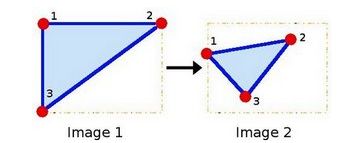
    对于每个点，都有两个对应的等式，一共有3个点，6个等式；对应$M$里面的6个参数，所以可以得到唯一的仿射矩阵$M$

---

代码

#include 
#include 

using namespace cv;
using namespace std;


int main(void)
{
	Mat src = imread("../res/lena.jpeg", cv::IMREAD_COLOR);
	if(src.empty())
	{
		cout << "cant't load image" << endl;
	}


//原图三个点
	Point2f srcTri[3];
	srcTri[0]=Point2f(0.f,0.f);
	srcTri[1]=Point2f(src.cols-1.f,0.f);
	srcTri[2]=Point2f(0.f,src.rows-1.f);

//目的图的三个点
	Point2f dstTri[3];
	dstTri[0]=Point2f(0.f,src.rows*0.33f);
	dstTri[1]=Point2f(src.cols*0.85f,src.rows*0.25f);
	dstTri[2]=Point2f(src.cols*0.15f,src.rows*0.7f);

//得到仿射矩阵	
	Mat warp_mat = getAffineTransform(srcTri,dstTri);

//通过仿射矩阵得到目的图像
	Mat warp_dst = Mat::zeros(src.rows,src.cols,src.type());
	warpAffine(src,warp_dst,warp_mat,warp_dst.size());

///旋转///

	Point center = Point(warp_dst.cols/2,warp_dst.rows/2); //定义旋转中心
	double angle = -50.0; //旋转角度，负数代表顺时针，单位度
	double scale = 1; //缩放比例

	Mat rot_mat = getRotationMatrix2D(center,angle,scale);  //由上面三个参数得到旋转矩阵

	Mat warp_rotate_dst;
	warpAffine(warp_dst,warp_rotate_dst,rot_mat,warp_dst.size()); //进行旋转操作

	imshow("source image" ,src);
	imshow("warp", warp_dst);
	imshow("warp+rotate",warp_rotate_dst);

	waitKey();

	return 0;
};

结果：第一张原图，第二张经过仿射变换之后，第三张再经过顺时针旋转50$°$的结果

---

OpenCV API

1. 计算仿射矩阵map_matrix ( 2×3)，

  Mat cv::getAffineTransform
  (
   const Point2f src[],     // 原图像的三个顶点
   const Point2f dst[]     //目的图像的三个顶点
   )

2. 对一幅图像进行仿射变换

void cv::warpAffine void cv::warpAffine
(
InputArray src,    // 原图
OutputArray dst,    // 目的图，大小是dsize，和原图类型一样
InputArray M,    // 2×3 的仿射变换矩阵
Size dsize,    // 输出图像大小
int flags = INTER_LINEAR,    // 插值方式
int borderMode = BORDER_CONSTANT,    // 边界处理方式
const Scalar & borderValue = Scalar()     // 如果是CONSTANT型border，此参数是边界的值
)

计算公式：

3. 计算旋转矩阵（2×3 ）

  Mat cv::getRotationMatrix2D
  (
   Point2f center,     //旋转中心
   double angle,    // 旋转角度（单位：$°$），正数  意味着逆时针
   double scale     //放大、缩小的比例
   )