二叉排序树(完整案例与完整C语言代码)

写在前面：博主是一位普普通通的19届双非软工在读生，平时最大的爱好就是听听歌，逛逛B站。博主很喜欢的一句话花开堪折直须折，莫待无花空折枝：博主的理解是头一次为人，就应该做自己想做的事，做自己不后悔的事，做自己以后不会留有遗憾的事，做自己觉得有意义的事，不浪费这大好的青春年华。博主写博客目的是记录所学到的知识并方便自己复习，在记录知识的同时获得部分浏览量，得到更多人的认可，满足小小的成就感，同时在写博客的途中结交更多志同道合的朋友，让自己在技术的路上并不孤单。

目录:
1.二叉排序树定义
2.二叉排序树查找
3.二叉排序树的插入
4.二叉排序树的删除
5.二叉排序树全功能完整代码实现
6.二叉排序树小结

1.二插排序树定义

二叉排序树要么是空二叉树，要么具有如下特点：

• 二叉排序树中，如果其根结点有左子树，那么左子树上所有结点的值都小于根结点的值；
• 二叉排序树中，如果其根结点有右子树，那么右子树上所有结点的值都大小根结点的值；
• 二叉排序树的左右子树也要求都是二叉排序树；

如下图就是一颗二叉排序树：

2.二叉排序树查找关键

二叉排序树中查找某关键字时，查找过程类似于次优二叉树，在二叉排序树不为空树的前提下，首先将被查找值同树的根结点进行比较，会有 3 种不同的结果：

• 如果相等，查找成功；
• 如果比较结果为根结点的关键字值较大，则说明该关键字可能存在其左子树中；
• 如果比较结果为根结点的关键字值较小，则说明该关键字可能存在其右子树中； 实现函数为：（运用递归的方法）:

BiTree SearchBST(BiTree T,KeyType key){
    //如果递归过程中 T 为空，则查找结果，返回NULL；或者查找成功，返回指向该关键字的指针
    if (!T || key==T->data) {
        return T;
    }else if(key<T->data){
        //递归遍历其左孩子
        return SearchBST(T->lchild, key);
    }else{
        //递归遍历其右孩子
        return SearchBST(T->rchild, key);
    }
}

3.二叉排序树中插入

二叉排序树本身是动态查找表的一种表示形式，有时会在查找过程中插入或者删除表中元素，当因为查找失败而需要插入数据元素时，该数据元素的插入位置一定位于二叉排序树的叶子结点，并且一定是查找失败时访问的最后一个结点的左孩子或者右孩子。

例如，在下图的二叉排序树中做查找关键字 1 的操作，当查找到关键字 3 所在的叶子结点时，判断出表中没有该关键字，此时关键字 1 的插入位置为关键字 3 的左孩子

所以，二叉排序树表示动态查找表做插入操作，只需要稍微更改一下上面的代码就可以实现，具体实现代码为：

BOOL SearchBST(BiTree T,KeyType key,BiTree f,BiTree *p){
    //如果 T 指针为空，说明查找失败，令 p 指针指向查找过程中最后一个叶子结点，并返回查找失败的信息
    if (!T){
        *p=f;
        return false;
    }
    //如果相等，令 p 指针指向该关键字，并返回查找成功信息
    else if(key==T->data){
        *p=T;
        return true;
    }
    //如果 key 值比 T 根结点的值小，则查找其左子树；反之，查找其右子树
    else if(key<T->data){
        return SearchBST(T->lchild,key,T,p);
    }else{
        return SearchBST(T->rchild,key,T,p);
    }
}
//插入函数
BOOL InsertBST(BiTree T,ElemType e){
    BiTree p=NULL;
    //如果查找不成功，需做插入操作
    if (!SearchBST(T, e,NULL,&p)) {
        //初始化插入结点
        BiTree s=(BiTree)malloc(sizeof(BiTree));
        s->data=e;
        s->lchild=s->rchild=NULL;
        //如果 p 为NULL，说明该二叉排序树为空树，此时插入的结点为整棵树的根结点
        if (!p) {
            T=s;
        }
        //如果 p 不为 NULL，则 p 指向的为查找失败的最后一个叶子结点，只需要通过比较 p 和 e 的值确定 s 到底是 p 的左孩子还是右孩子
        else if(e<p->data){
            p->lchild=s;
        }else{
            p->rchild=s;
        }
        return true;
    }
    //如果查找成功，不需要做插入操作，插入失败
    return false;
}

通过使用二叉排序树对动态查找表做查找和插入的操作，同时在中序遍历二叉排序树时，可以得到有关所有关键字的一个有序的序列。

例如，假设原二叉排序树为空树，在对动态查找表 {3，5，7，2，1} 做查找以及插入操作时，可以构建出一个含有表中所有关键字的二叉排序树，过程如：

当使用中序遍历算法遍历二叉排序树时，得到的序列为：1 2 3 5 7 ，为有序序列。

一个无序序列可以通过构建一棵二叉排序树，从而变成一个有序序列。

4.二叉排序树的删除

在查找过程中，如果在使用二叉排序树表示的动态查找表中删除某个数据元素时，需要在成功删除该结点的同时，依旧使这棵树为二叉排序树。

假设要删除的为结点 p，则对于二叉排序树来说，需要根据结点 p 所在不同的位置作不同的操作，有以下 3 种可能：

1. 结点 p 为叶子结点，此时只需要删除该结点，并修改其双亲结点的指针即可；
2. 结点 p 只有左子树或者只有右子树，此时只需要将其左子树或者右子树直接变为结点 p 双亲结点的左子树即可；
3. 结点 p 左右子树都有，此时有两种处理方式

当p左右孩子都有的情况下，第一种处理方式：令结点 p 的左子树为其双亲结点的左子树；结点 p 的右子树为其自身直接前驱结点的右子树

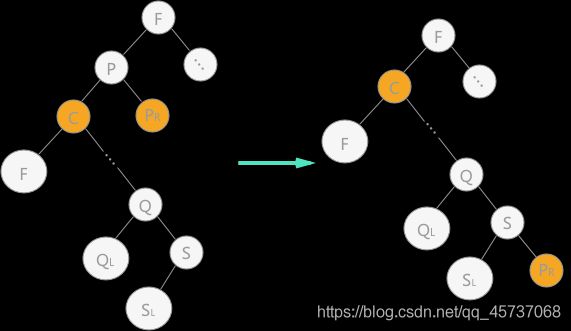
第二种方式：用结点 p 的直接前驱（或直接后继）来代替结点 p，同时在二叉排序树中对其直接前驱（或直接后继）做删除操作。如图 4 为使用直接前驱代替结点 p：

在对左图进行中序遍历时，得到的结点 p 的直接前驱结点为结点 s，所以直接用结点 s 覆盖结点 p，由于结点 s 还有左孩子，根据第 2 条规则，直接将其变为双亲结点的右孩子

第一种方法可能增加树的高度，后一种方法是以删除结点左子树中关键字最大的结点替代被删结点，然后从左子树中删除这个结点，此结点一定没有右子树，不会增加树的高度，所以一般采用后一种方法处理

int Delete(BiTree *p)
{
    BiTree q, s;
    //情况 1，结点 p 本身为叶子结点，直接删除即可
    if(!(*p)->lchild && !(*p)->rchild){
        *p = NULL;
    }
    else if(!(*p)->lchild){ //左子树为空，只需用结点 p 的右子树根结点代替结点 p 即可；
        q = *p;
        *p = (*p)->rchild;
        free(q);
    }
    else if(!(*p)->rchild){//右子树为空，只需用结点 p 的左子树根结点代替结点 p 即可；
        q = *p;
        *p = (*p)->lchild;//这里不是指针 *p 指向左子树，而是将左子树存储的结点的地址赋值给指针变量 p
        free(q);
    }
    else{//左右子树均不为空，采用第 2 种方式
        q = *p;
        s = (*p)->lchild;
        //遍历，找到结点 p 的直接前驱
        while(s->rchild)
        {
            q = s;
            s = s->rchild;
        }
        //直接改变结点 p 的值
        (*p)->data = s->data;
        //判断结点 p 的左子树 s 是否有右子树，分为两种情况讨论
        if( q != *p ){
            q->rchild = s->lchild;//若有，则在删除直接前驱结点的同时，令前驱的左孩子结点改为 q 指向结点的孩子结点
        }else{
            q->lchild = s->lchild;//否则，直接将左子树上移即可
        }
        free(s);
    }
    return TRUE;
}
int DeleteBST(BiTree *T, int key)
{
    if( !(*T)){//不存在关键字等于key的数据元素
        return FALSE;
    }
    else
    {
        if( key == (*T)->data ){
            Delete(T);
            return TRUE;
        }
        else if( key < (*T)->data){
            //使用递归的方式
            return DeleteBST(&(*T)->lchild, key);
        }
        else{
            return DeleteBST(&(*T)->rchild, key);
        }
    }
}

5.二叉排序树全功能完整代码实现

#include
#include
#define TRUE 1
#define FALSE 0
#define ElemType int
#define  KeyType int
/* 二叉排序树的节点结构定义 */
typedef struct BiTNode
{
    int data;
    struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;

//二叉排序树查找算法
int SearchBST(BiTree T,KeyType key,BiTree f,BiTree *p){
    //如果 T 指针为空，说明查找失败，令 p 指针指向查找过程中最后一个叶子结点，并返回查找失败的信息
    if (!T){
        *p=f;
        return FALSE;
    }
    //如果相等，令 p 指针指向该关键字，并返回查找成功信息
    else if(key==T->data){
        *p=T;
        return TRUE;
    }
    //如果 key 值比 T 根结点的值小，则查找其左子树；反之，查找其右子树
    else if(key<T->data){
        return SearchBST(T->lchild,key,T,p);
    }else{
        return SearchBST(T->rchild,key,T,p);
    }
}
int InsertBST(BiTree *T,ElemType e){
    BiTree p=NULL;
    //如果查找不成功，需做插入操作
    if (!SearchBST((*T), e,NULL,&p)) {
        //初始化插入结点
        BiTree s=(BiTree)malloc(sizeof(BiTree));
        s->data=e;
        s->lchild=s->rchild=NULL;
        //如果 p 为NULL，说明该二叉排序树为空树，此时插入的结点为整棵树的根结点
        if (!p) {
            *T=s;
        }
        //如果 p 不为 NULL，则 p 指向的为查找失败的最后一个叶子结点，只需要通过比较 p 和 e 的值确定 s 到底是 p 的左孩子还是右孩子
        else if(e < p->data){
            p->lchild=s;
        }else{
            p->rchild=s;
        }
        return TRUE;
    }
    //如果查找成功，不需要做插入操作，插入失败
    return FALSE;
}
//删除函数
int Delete(BiTree *p)
{
    BiTree q, s;
    //情况 1，结点 p 本身为叶子结点，直接删除即可
    if(!(*p)->lchild && !(*p)->rchild){
        *p = NULL;
    }
    else if(!(*p)->lchild){ //左子树为空，只需用结点 p 的右子树根结点代替结点 p 即可；
        q = *p;
        *p = (*p)->rchild;
        free(q);
    }
    else if(!(*p)->rchild){//右子树为空，只需用结点 p 的左子树根结点代替结点 p 即可；
        q = *p;
        *p = (*p)->lchild;//这里不是指针 *p 指向左子树，而是将左子树存储的结点的地址赋值给指针变量 p
        free(q);
    }
    else{//左右子树均不为空，采用第 2 种方式
        q = *p;
        s = (*p)->lchild;
        //遍历，找到结点 p 的直接前驱
        while(s->rchild)
        {
            q = s;
            s = s->rchild;
        }
        //直接改变结点 p 的值
        (*p)->data = s->data;
        //判断结点 p 的左子树 s 是否有右子树，分为两种情况讨论
        if( q != *p ){
            q->rchild = s->lchild;//若有，则在删除直接前驱结点的同时，令前驱的左孩子结点改为 q 指向结点的孩子结点
        }else{
            q->lchild = s->lchild;//否则，直接将左子树上移即可
        }
        free(s);
    }
    return TRUE;
}
int DeleteBST(BiTree *T, int key)
{
    if( !(*T)){//不存在关键字等于key的数据元素
        return FALSE;
    }
    else
    {
        if( key == (*T)->data ){
            Delete(T);
            return TRUE;
        }
        else if( key < (*T)->data){
            //使用递归的方式
            return DeleteBST(&(*T)->lchild, key);
        }
        else{
            return DeleteBST(&(*T)->rchild, key);
        }
    }
}
void order(BiTree t)//中序输出
{
    if(t == NULL){
        return ;
    }
    order(t->lchild);
    printf("%d ", t->data);
    order(t->rchild);
}
int main()
{
    int i;
    int a[5] = {3,4,2,5,9};
    BiTree T = NULL;
    for( i = 0; i < 5; i++ ){
        InsertBST(&T, a[i]);
    }
    printf("中序遍历二叉排序树：\n");
    order(T);
    printf("\n");
    printf("删除3后，中序遍历二叉排序树：\n");
    DeleteBST(&T,3);
    order(T);
}
//
中序遍历二叉排序树：
2 3 4 5 9
删除3后，中序遍历二叉排序树：
2 4 5 9

6.二叉排序树小结

使用二叉排序树在查找表中做查找操作的时间复杂度同建立的二叉树本身的结构有关。即使查找表中各数据元素完全相同，但是不同的排列顺序，构建出的二叉排序树大不相同。

例如：查找表 {45，24，53，12，37，93} 和表 {12，24，37，45，53，93} 各自构建的二叉排序树图下图所示：

使用二叉排序树实现动态查找操作的过程，实际上就是从二叉排序树的根结点到查找元素结点的过程，所以时间复杂度同被查找元素所在的树的深度（层次数）有关。