Python描述数据结构之KMP篇
文章目录
- 前言
- 1. BF算法
- 2. KMP算法
- 3. KMP算法优化版
- 结束语
前言
本篇章主要介绍串的KMP模式匹配算法及其改进,并用Python实现KMP算法。
1. BF算法
BF算法,即 B r u c e − F o r c e Bruce-Force Bruce−Force算法,又称暴力匹配算法。其思想就是将主串S的第一个字符与模式串T的第一个字符进行匹配,若相等,则继续比较S的第二个字符和T的第二个字符;若不相等,则比较S的第二个字符和T的第一个字符,依次比较下去,直到得出最后的匹配结果。
假设主串 S = A B A C A B A B S=ABACABAB S=ABACABAB,模式串 T = A B A B T=ABAB T=ABAB,每趟匹配失败后,主串S指针回溯,模式串指针回到头部,然后再次匹配,过程如下:
def BF(substrS, substrT):
if len(substrT) > len(substrS):
return -1
j = 0
t = 0
while j < len(substrS) and t < len(substrT):
if substrT[t] == substrS[j]:
j += 1
t += 1
else:
j = j - t + 1
t = 0
if t == len(substrT):
return j - t
else:
return -1
2. KMP算法
KMP算法,是由 D . E . K n u t h 、 J . H . M o r r i s 、 V . R . P r a t t D.E.Knuth、J.H.Morris、V.R.Pratt D.E.Knuth、J.H.Morris、V.R.Pratt同时发现的,又被称为克努特-莫里斯-普拉特算法。该算法的基本思路就是在匹配失败后,无需回到主串和模式串最近一次开始比较的位置,而是在不改变主串已经匹配到的位置的前提下,根据已经匹配的部分字符,从模式串的某一位置开始继续进行串的模式匹配。
就是这次匹配失败时,下次匹配时模式串应该从哪一位开始比较。
BF算法思路简单,便于理解,但是在执行时效率太低。在上述的匹配过程中,第一次匹配时已经匹配的 " A B A " "ABA" "ABA",其前缀与后缀都是 " A " "A" "A",这个时候我们就不需要执行第二次匹配了,因为第一次就已经匹配过了,所以可以跳过第二次匹配,直接进行第三次匹配,即前缀位置移到后缀位置,主串指针无需回溯,并继续从该位开始比较。
前缀:是指除最后一个字符外,字符串的所有头部子串。
后缀:是指除第一个字符外,字符串的所有尾部子串。
部分匹配值 ( P a r t i a l (Partial (Partial M a t c h , P M ) Match,PM) Match,PM):字符串的前缀和后缀的最长相等前后缀长度。
例如, ′ a ′ 'a' ′a′的前缀和后缀都为空集,则最长公共前后缀长度为0; ′ a b ′ 'ab' ′ab′的前缀为 { a } \{a\} {a},后缀为 { b } \{b\} {b},则最长公共前后缀为空集,其长度长度为0; ′ a b a ′ 'aba' ′aba′的前缀为 { a , a b } \{a,ab\} {a,ab},后缀为 { a , b a } \{a,ba\} {a,ba},则最长公共前后缀为 { a } \{a\} {a},其长度长度为1; ′ a b a b ′ 'abab' ′abab′的前缀为 { a , a b , a b a } \{a,ab,aba\} {a,ab,aba},后缀为 { b , a b , b a b } \{b,ab,bab\} {b,ab,bab},则最长公共前后缀为 { a b } \{ab\} {ab},其长度长度为2。
前缀一定包含第一个字符,后缀一定包含最后一个字符。
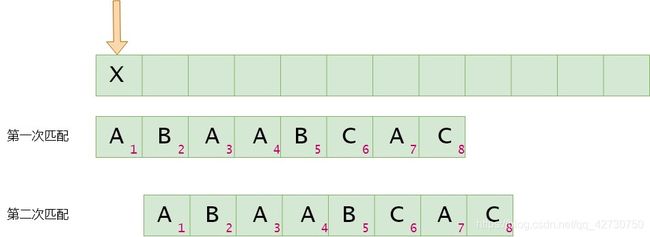
如果模式串1号位与主串当前位(箭头所指的位置)不匹配,将模式串1号位与主串的下一位进行比较。next[0]=-1,这边就是一个特殊位置了,即如果主串与模式串的第1位不相同,那么下次就直接比较各第2位的字符。
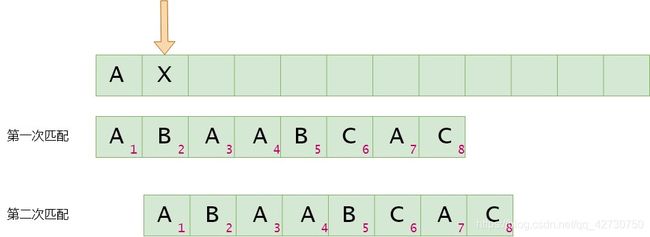
如果模式串2号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为 " A " "A" "A",即最长公共前后缀为空集,其长度为0,则下次匹配时将模式串1号位与主串的当前位进行比较。next[1]=0

如果模式串3号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为 " A B " "AB" "AB",即最长公共前后缀为空集,其长度为0,则下次匹配时将模式串1号位与主串的当前位进行比较。next[2]=0

如果模式串4号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为 " A B A " "ABA" "ABA",即最长公共前后缀为 " A " "A" "A",其长度为1,则下次匹配时将前缀位置移到后缀位置,即模式串2号位与主串的当前位进行比较。next[3]=1
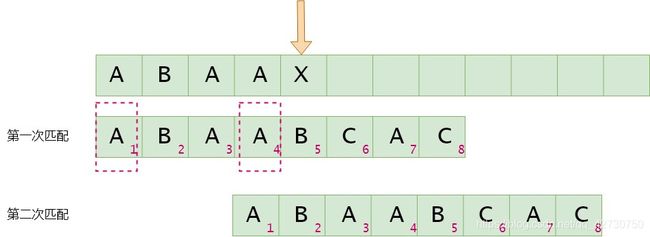
如果模式串5号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为 " A B A A " "ABAA" "ABAA",即最长公共前后缀为 " A " "A" "A",其长度为1,则下次匹配时将前缀位置移到后缀位置,即模式串2号位与主串的当前位进行比较。next[4]=1
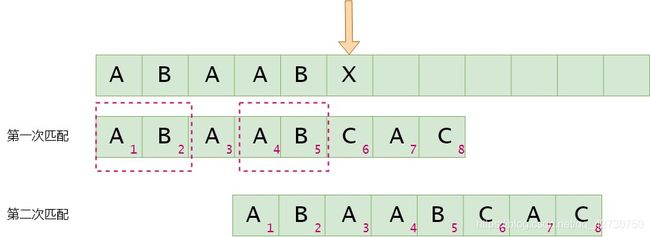
如果模式串6号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为 " A B A A B " "ABAAB" "ABAAB",即最长公共前后缀为 " A B " "AB" "AB",其长度为2,则下次匹配时将前缀位置移到后缀位置,即模式串3号位与主串的当前位进行比较。next[5]=2
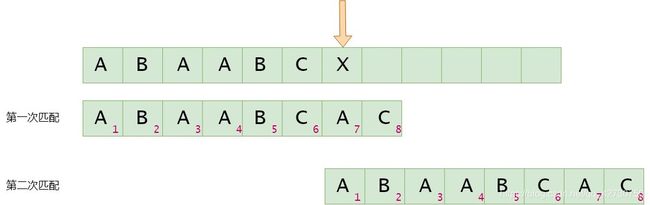
如果模式串7号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为 " A B A A B C " "ABAABC" "ABAABC",即最长公共前后缀为空集,其长度为0,则下次匹配时将模式串1号位与主串的当前位进行比较。next[6]=0

如果模式串8号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为 " A B A A B C A " "ABAABCA" "ABAABCA",即最长公共前后缀为 " A " "A" "A",其长度为1,则下次匹配时将模式串2号位与主串的当前位进行比较。next[7]=1
综上,可以得到模式串的next数组,发现没有,把主串去掉也可以得到这个数组,即下次匹配时模式串向后移动的位数与主串无关,仅与模式串本身有关。
| 位编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 索引 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 模式串 | A | B | A | A | B | C | A | C |
| next | -1 | 0 | 0 | 1 | 1 | 2 | 0 | 1 |
next数组,即存放的是每个字符匹配失败时,对应的下一次匹配时模式串开始匹配的位置。
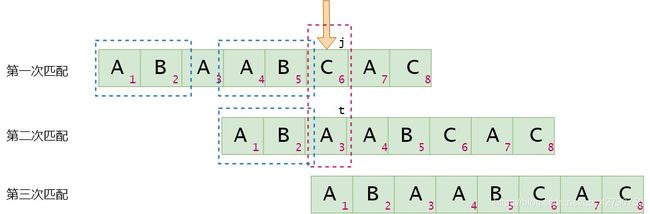
如何在代码里实现上述流程呢?举个栗子,蓝色方框圈出的就是公共前后缀,假设next[j]=t:
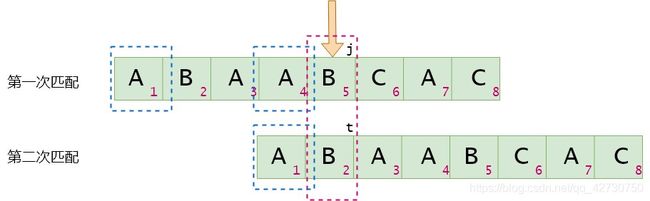
当 T j = T t T_j=T_t Tj=Tt时,可以得到 n e x t [ j + 1 ] = t + 1 = n e x t [ j ] + 1 next[j+1]=t+1=next[j]+1 next[j+1]=t+1=next[j]+1。这个时候 j = 4 , t = 1 j=4,t=1 j=4,t=1(索引);
当 T j ≠ T t T_j \neq T_t Tj=Tt时,即模式串 t t t位置与主串(并不是真正的主串)不匹配,则将下面的那个模式串移动到 n e x t [ t ] next[t] next[t]位置进行比较,即 t = n e x t [ t ] t=next[t] t=next[t],直到 T j = T t T_j=T_t Tj=Tt或 t = − 1 t=-1 t=−1,当 t = − 1 t=-1 t=−1时, n e x t [ j + 1 ] = 0 next[j+1]=0 next[j+1]=0。这里就是 t = n e x t [ 2 ] = 0 t=next[2]=0 t=next[2]=0,即下次匹配时,模式串的第1位与主串当前位进行比较。
代码如下:
def getNext(substrT):
next_list = [-1 for i in range(len(substrT))]
j = 0
t = -1
while j < len(substrT) - 1:
if t == -1 or substrT[j] == substrT[t]:
j += 1
t += 1
# Tj=Tt, 则可以到的next[j+1]=t+1
next_list[j] = t
else:
# Tj!=Tt, 模式串T索引为t的字符与当前位进行匹配
t = next_list[t]
return next_list
def KMP(substrS, substrT, next_list):
count = 0
j = 0
t = 0
while j < len(substrS) and t < len(substrT):
if substrS[j] == substrT[t] or t == -1:
# t == -1目的就是第一位匹配失败时
# 主串位置加1, 匹配串回到第一个位置(索引为0)
# 匹配成功, 主串和模式串指针都后移一位
j += 1
t += 1
else:
# 匹配失败, 模式串索引为t的字符与当前位进行比较
count += 1
t = next_list[t]
if t == len(substrT):
# 这里返回的是索引
return j - t, count+1
else:
return -1, count+1
3. KMP算法优化版
上面定义的next数组在某些情况下还有些缺陷,发现没有,在第一个图中,我们还可以跳过第3次匹配,直接进行第4次匹配。为了更好地说明问题,我们以下面这种情况为例,来优化一下KMP算法。假设主串 S = A A A B A A A A B S=AAABAAAAB S=AAABAAAAB,模式串 T = A A A A B T=AAAAB T=AAAAB,按照KMP算法,匹配过程如下:
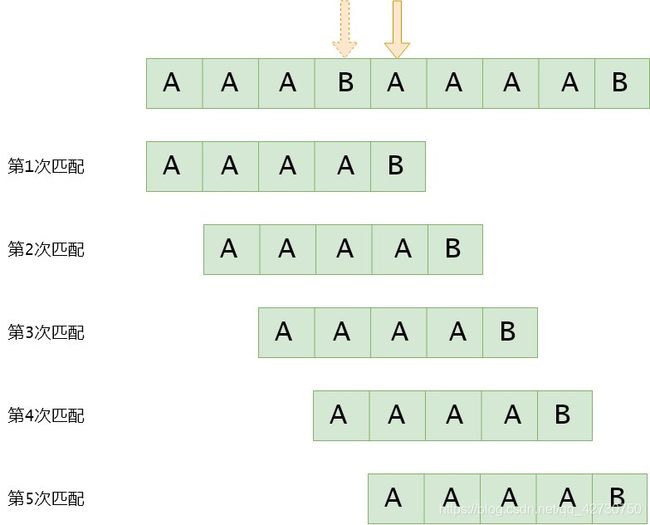
可以看到第2、3、4次的匹配是多余的,因为我们在第一次匹配时,主串 S S S的4号位为模式串 T T T的4号位就已经比较了,且 T 3 ≠ S 3 T_3 \neq S_3 T3=S3,又因为模式串 T T T的4号位与其1、2、3号位的字符一样,即 T 3 = T 2 = T 1 = T 0 ≠ S 3 T_3=T_2=T_1=T_0 \neq S_3 T3=T2=T1=T0=S3,所以可以直接进入第5次匹配。
那么,问题出在哪里???我们结合着next数组看一下:
| 位编号 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 索引 | 0 | 1 | 2 | 3 | 4 |
| 模式串 | A | A | A | A | B |
| next | -1 | 0 | 1 | 2 | 3 |
问题在于,当 T j ≠ S j T_j \neq S_j Tj=Sj时,下次匹配的必然是 T n e x t [ j ] T_{next[j]} Tnext[j]与 S j S_j Sj,如果这时 T n e x t [ j ] = T j T_{next[j]} = T_j Tnext[j]=Tj,那么又相当于 T j T_j Tj与 S j S_j Sj进行比较,因为它们的字符一样,毫无疑问,这次匹配是没有意义的,应当将 n e x t [ j ] next[j] next[j]的值直接赋值为-1,即遇到这种情况,主串与模式串都从下一位开始比较。
所以,我们要修正一下next数组。
大致流程和上面求解next数组时一样,这里就是多了一个判别条件,如果在匹配时出现了 T n e x t [ j ] = T j T_{next[j]} = T_j Tnext[j]=Tj,我们就将next[j]更新为next [ \Big[ [next[j] ] \Big] ],直至两者不相等为止(相当于了迭代)。在代码里面实现就是,如果某个字符已经相等或者第一个next[j]数组值为-1(即 t = − 1 t=-1 t=−1),且主串和模式串指针各后移一位时的字符仍然相同,那么就将当前的next[j]值更新为上一个next[j]数组值,更新后的数组命名为nextval。
代码如下:
def getNextval(substrT):
nextval_list = [-1 for i in range(len(substrT))]
j = 0
t = -1
while j < len(substrT) - 1:
if t == -1 or substrT[j] == substrT[t]:
j += 1
t += 1
if substrT[j] != substrT[t]:
# Tj=Tt, 但T(j+1)!=T(t+1), 这个就和next数组计算时是一样的
# 可以得到nextval[j+1]=t+1
nextval_list[j] = t
else:
# Tj=Tt, 且T(j+1)==T(t+1), 这个就是next数组需要更新的
# nextval[j+1]=上一次的nextval_list[t]
nextval_list[j] = nextval_list[t]
else:
# 匹配失败, 模式串索引为t的字符与当前位进行比较
t = nextval_list[t]
return nextval_list
对KMP的优化其实就是对next数组的优化,修正后的next数组,即nextval数组如下:
| 位编号 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 索引 | 0 | 1 | 2 | 3 | 4 |
| 模式串 | A | A | A | A | B |
| nextval | -1 | -1 | -1 | -1 | 3 |
下面就测试一下:
if __name__ == '__main__':
S1 = 'ABACABAB'
T1 = 'ABAB'
S2 = 'AAABAAAAB'
T2 = 'AAAAB'
print('*' * 50)
print('主串S={0}与模式串T={1}进行匹配'.format(S1, T1))
print('{:*^25}'.format('KMP'))
next_list1 = getNext(T1)
print('next数组为: {}'.format(next_list1))
index1_1, count1_1 = KMP(S1, T1, next_list1)
print('匹配到的位置(索引): {}, 匹配次数: {}'.format(index1_1, count1_1))
print('{:*^25}'.format('KMP优化版'))
nextval_list1 = getNextval(T1)
print('nextval数组为: {}'.format(nextval_list1))
index1_2, count1_2 = KMP(S1, T1, nextval_list1)
print('匹配到的位置(索引): {}, 匹配次数: {}'.format(index1_2, count1_2))
print('')
print('*' * 50)
print('主串S={0}与模式串T={1}进行匹配'.format(S2, T2))
print('{:*^25}'.format('KMP'))
next_list2 = getNext(T2)
print('next数组为: {}'.format(next_list2))
index2_1, count2_1 = KMP(S2, T2, next_list2)
print('匹配到的位置(索引): {}, 匹配次数: {}'.format(index2_1, count2_1))
print('{:*^25}'.format('KMP优化版'))
nextval_list2 = getNextval(T2)
print('nextval数组为: {}'.format(nextval_list2))
index2_2, count2_2 = KMP(S2, T2, nextval_list2)
print('匹配到的位置(索引): {}, 匹配次数: {}'.format(index2_2, count2_2))
运行结果如下:
运行的结果和我们分析的是一样的,不修正next数组时,主串 S = A B A C A B A B S=ABACABAB S=ABACABAB与模式串 T = A B A B T=ABAB T=ABAB匹配时需要4次,主串 S = A A A B A A A A B S=AAABAAAAB S=AAABAAAAB与模式串 T = A A A A B T=AAAAB T=AAAAB匹配时需要5次;修正next数组后,主串 S = A B A C A B A B S=ABACABAB S=ABACABAB与模式串 T = A B A B T=ABAB T=ABAB匹配时需要3次,主串 S = A A A B A A A A B S=AAABAAAAB S=AAABAAAAB与模式串 T = A A A A B T=AAAAB T=AAAAB匹配时仅需要2次。
结束语
在写本篇博客之前也是反复看参考书、视频,边画图边去理解它,这篇博客也是反复修改了好几次,最终算是把KMP解决掉了,有关字符串知识的复习也算是基本结束,下面就是刷题了(虽然在LeetCode做过了几道题)。
本篇博客也仅是在自己的理解基础上写的,难免出错,有问题欢迎交流,共同进步哦ヾ(๑╹◡╹)ノ"