字符串匹配之KMP算法(Python)
字符串的模式匹配
我们把在串S中寻找与串T相等的子串的过程称为串的模式匹配,其中串S被称为主串,串T被称为模式串。若在串S中找到与串T相等的子串,则匹配成功;否则匹配失败。模式匹配的典型应用有搜索引擎、拼写检查、语言翻译和数据压缩等。在下文中将通过例题介绍串实现模式匹配的方法–KMP算法。
过程
KMP算法与暴力解法(BF算法)的区别在于匹配失败后,主串指针 i 不用回溯,只需要改变模式串中的 j ,从而减少匹配次数,以提高匹配模式的效率。
记主串比较字符位置为 i ,模式串比较字符串位置为 j 。
暴力解法和kmp匹配过程如下图:
暴力解法
KMP算法
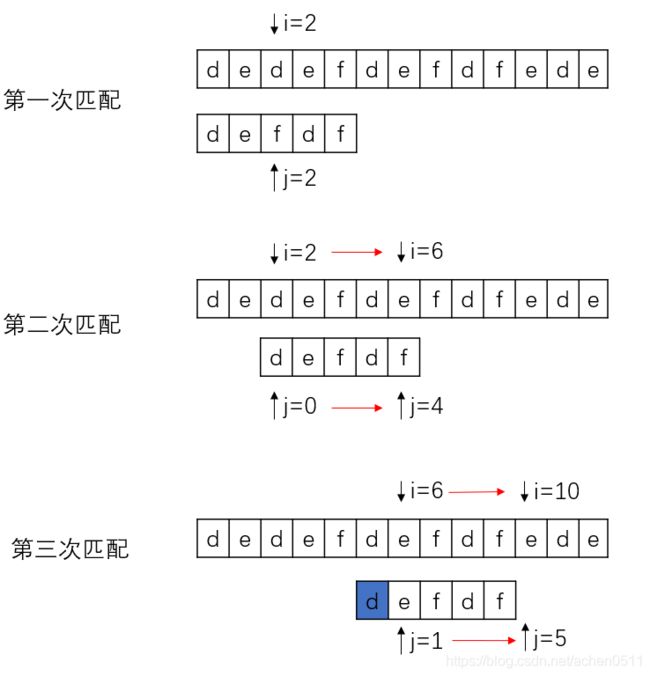
暴力解法的思路很容易理解:
即主串的 i = 0 的位置开始匹配模式串,每次匹配失败后,就从 i + 1 处重新进行匹配,直到匹配成功或者未找到与模式串匹配的子串为止。但是从上图的过程中很容易看出暴力解法(BF算法)的第二、四、五次匹配过程明显是不必要的,因为这几次过程模式串与主串显然u不匹配。
因此,KMP算法基于这一点进行优化:
即每次匹配失败后,下一次的匹配过程主串位置指针 i 不再回溯,而是从匹配失败的位置开始(如上图的第一次和第二次匹配过程),并且模式串位置指针 j 尽量不回溯(如上图第二、三次匹配过程),这样一来就大大提高了匹配的效率。
但是这样一来,问题又出现了:指针 i 不变时,下一次的模式串位置指针 j 应该指向哪个位置?这里就要引出一个字符串前后缀的概念。
最长公共前后缀
字符串的前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串;后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串;最长公共前后缀是指字符串的最长的相等的前后缀。
例如 字符串"ab", 前缀为a,后缀为b,无最长公共前后缀为,长度为0
字符串“aba”,前缀有{a,ab},后缀有{a,ba},最长公共前后缀为a,长度为1
字符串“abab”,前缀有{a,ab,aba},后缀有{b,ab,bab},最长公共前后缀ab,长度为2
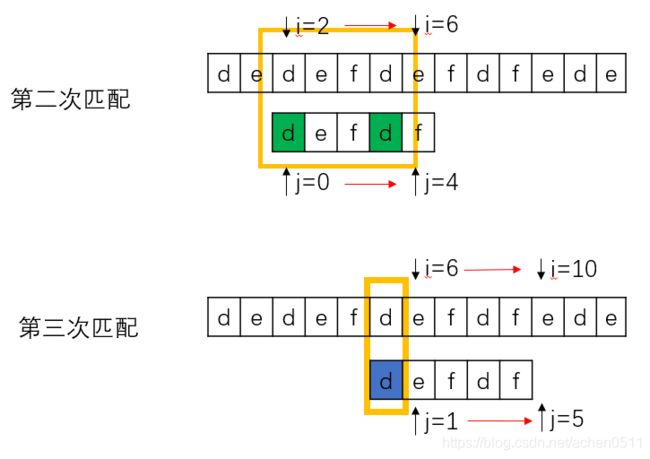
回到上面的问题:指针 i 不变时,下一次的模式串位置指针 j 应该指向哪个位置?
观察例子中的第二次匹配过程(如上图),模式串在 j = 4,也就是 f 的时候匹配失败,而此时取模式串子串 [0: (j-1)] 也就是“defd”,取其最长公共前后缀为d。然后再看第三次匹配过程,你就会神奇的发现主串的 i - 1 和模式串的 j - 1 也就是“d”,是一样的,这就是最长公共前后缀在这个过程的作用,记最长公共前后缀的长度为 k ,前后缀的相同使得在下一次匹配的过程中模式串的前 k 个字符无需再次匹配,直接从k+1的位置开始匹配即可。那么我们创建一个next数组来储存模式串的每个子串的“k+1”也就是每个字符匹配失败是对应的下一次匹配的起始位置(有点拗口,多看两遍)。如下图:(为什么next[0] = -1留到实现next数组时解释)

KMP算法框架
至此,KMP算法实现字符串匹配的思路大体已成,假定已经实现next数组,我们先把实现KMP算法的框架写出来:
def kmp(m_str, s_str):
# m_str表示主串,s_str表示模式串
i = j = 0 # i,j位置指针初始值为0
while i < len(m_str) and j < len(s_str):
# 模式串遍历结束匹配成功,主串遍历结束匹配失败
# 匹配成功或失败后退出
if m_str[i] == s_str[j]:
i += 1
j += 1
else:
j = next_ls[j]
if j == len(s_str):
return i - j # 匹配成功
return -1 # 匹配失败
以上就是KMP算法的基本框架。
实现next数组
那么下面来讨论如何实现next数组以及为什么next[0]=-1 而不是等于0
首先,为什么next[0]=-1 而不是等于0,其实原因在于当next[0]时,上面的基本框架就会陷入死循环,因此我们把-1赋值到next[0],当首字母匹配失败时令 j = -1 时,然后其自增,也就是令j=0,就实现了 i 指针往后移,j 指针归零的效果。当然基本框架也会因此有些微调:
def kmp(m_str, s_str):
# m_str表示主串,s_str表示模式串
i = j = 0 # i,j位置指针初始值为0
while i < len(m_str) and j < len(s_str):
# 模式串遍历结束匹配成功,主串遍历结束匹配失败
# 匹配成功或失败后退出
if m_str[i] == s_str[j] or j == -1:
# 把j==-1时纳入到条件判断中,实现i+1,j归零
i += 1
j += 1
else:
j = next_ls[j]
if j == len(s_str):
return i - j # 匹配成功
return -1 # 匹配失败
再然后要如何用代码实现next数组:
实际上仔细思考上面的next数组的求值过程,你会惊奇的发现–其实求next数组的值也就是最长公共前后缀的过程也是一个匹配的过程,kmp算法不就是用来实现匹配的嘛,所以next数组的实现跟kmp也有莫大关系,下面我们用实例体验一波:
eg.求出模式串“abababca”的next数组(可以自己先手动算一波,在进行验证)
(图片中的Str行最后一个是小写的a,打错了,图片不好改T-T)
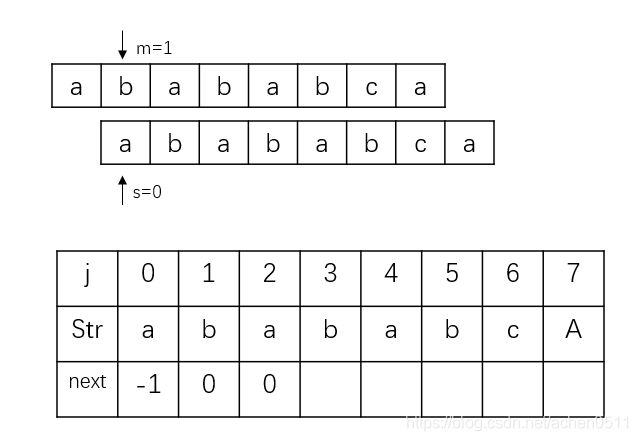
由于next[0]=-1,且单字符没有最长公共前后后缀,所以next[1]=0。因此我们直接从next[2]开始求值,因为str[m]->"b"不等于(下面用!=表示)str[s]->“a”,所以根据上面的基本框架匹配失败则返回next_ls[ s ] ( 这里的指针是 s 而不是 j ),所以next[ s ] = next[0] = -1,???似乎哪里不对,没错,当 j == -1 要进行一次自增,所以next[0] = -1+1=0,这就是正确答案了。然后进行下一次匹配:
在这一次的匹配中Str[m]->“a” == Str[s]->“a”,匹配成功,所以按照前面kmp基本框架匹配成功后 i+=1,j+=1。因此得next[3]=1,进行下一次匹配:
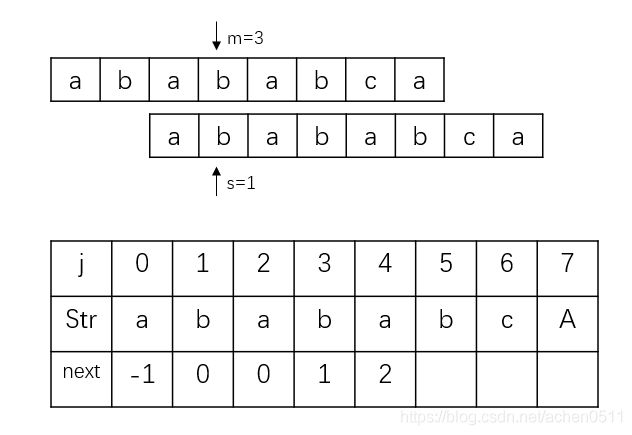
第三次匹配,Str[m]->“b” == Str[s]->“b”,匹配成功,i+1,j+1,所以next[4]=2,进行下一次匹配:
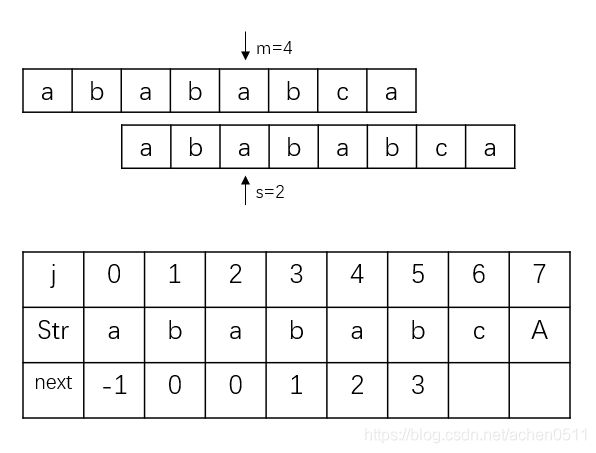
第四次匹配,Str[m]->“a” == Str[s]->“a”,匹配成功,i+1,j+1,所以next[5]=3,进行下一次匹配:
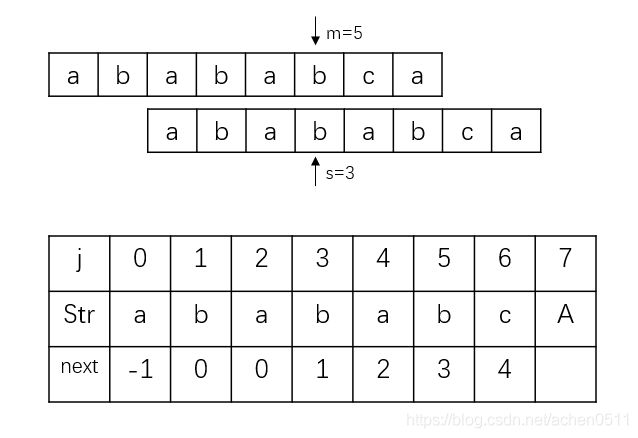
第五次匹配,Str[m]->“b” == Str[s]->“b”,匹配成功,i+1,j+1,所以next[6]=4,进行下一次匹配:
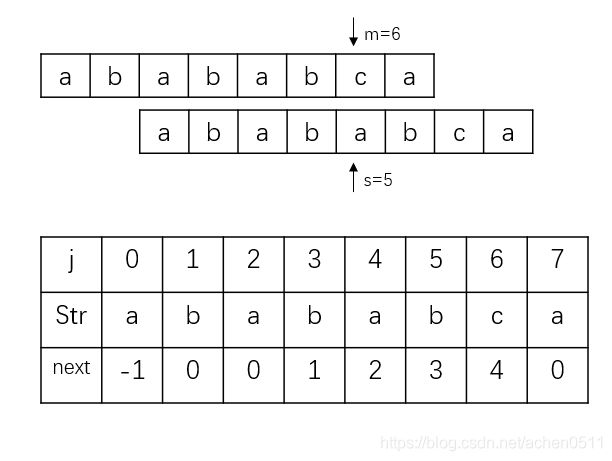
第五次匹配,Str[m]->“c” != Str[s]->“a”,匹配失败,根据上面的基本框架,匹配失败后 s = next[s]=3,然后继续循环匹配Str[6]->“c” != Str[3]->“b”,匹配失败s = next[s]=1,继续匹配Str[6]->“c” != Str[1]->“b”,匹配失败,s = next[s]=0,继续匹配,Str[6]->“c” != Str[0]->“a”,匹配失败,s =next[s]=-1,自增得s=-1+1=0,所以next[7]=0。
至此,大功告成!!!代码如下:
def kmp(m_str, s_str):
# m_str表示主串,s_str表示模式串
# 求next数组
next_ls = [-1]*len(s_str)
m = 1 # 从1开始匹配
s = 0
next_ls[1]=0
while m<len(s_str)-1:
if s_str[m] == s_str[s] or s == -1:
m += 1
s += 1
next_ls[m] = s
else:
s = next_ls[s]
# print(next_ls) 检查next数组
# KMP
i = j = 0 # i,j位置指针初始值为0
while i < len(m_str) and j < len(s_str):
# 模式串遍历结束匹配成功,主串遍历结束匹配失败
# 匹配成功或失败后退出
if m_str[i] == s_str[j] or j == -1:
# 把j==-1时纳入到条件判断中,实现i+1,j归零
i += 1
j += 1
else:
j = next_ls[j]
if j == len(s_str):
return i - j # 匹配成功
return -1 # 匹配失败
#测试
print(kmp('decdagee','age'))
#结果
[-1, 0, 0]
4
憋了好久,总算没有鸽掉,以上就是我对KMP算法的理解,如有不足或者错误之处,敬请指出。