平衡二叉排序树(完整案例详解及完整C代码实现)

写在前面：博主是一位普普通通的19届双非软工在读生，平时最大的爱好就是听听歌，逛逛B站。博主很喜欢的一句话花开堪折直须折，莫待无花空折枝：博主的理解是头一次为人，就应该做自己想做的事，做自己不后悔的事，做自己以后不会留有遗憾的事，做自己觉得有意义的事，不浪费这大好的青春年华。博主写博客目的是记录所学到的知识并方便自己复习，在记录知识的同时获得部分浏览量，得到更多人的认可，满足小小的成就感，同时在写博客的途中结交更多志同道合的朋友，让自己在技术的路上并不孤单。

目录:
1.平衡二叉树简介
2.二叉排序树转换平衡为平衡二叉树
3.不平衡因子的四种情况
4.构建平衡二叉树的代码实现

1.平衡二叉树简介

平衡二叉树，又称为 AVL 树。实际上就是遵循以下两个特点的二叉树：

• 每棵子树中的左子树和右子树的深度差不能超过 1；
• 二叉树中每棵子树都要求是平衡二叉树；

其实就是在二叉树的基础上，若树中每棵子树都满足其左子树和右子树的深度差都不超过 1，则这棵二叉树就是平衡二叉树。

如下图所示，其中 （a） 的两棵二叉树中由于各个结点的平衡因子数的绝对值都不超过 1，所以 （a） 中两棵二叉树都是平衡二叉树；而 （b） 的两棵二叉树中有结点的平衡因子数的绝对值超过 1，所以都不是平衡二叉树。

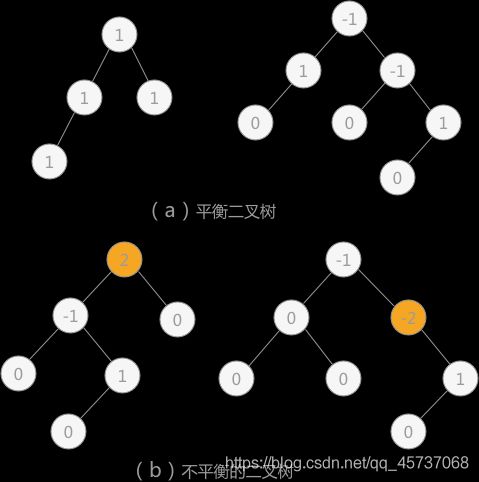
平衡因子：每个结点都有其各自的平衡因子，表示的就是其左子树深度同右子树深度的差。平衡二叉树中各结点平衡因子的取值只可能是：0、1 和 -1。

2.二叉排序树转换平衡为平衡二叉树

为了排除动态查找表中不同的数据排列方式对算法性能的影响，需要考虑在不会破坏二叉排序树本身结构的前提下，将二叉排序树转化为平衡二叉树。

例如，使用上一节的算法在对查找表{13，24，37，90，53}构建二叉排序树时，当插入 13 和 24 时，二叉排序树此时还是平衡二叉树：

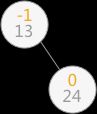
当继续插入 37 时，生成的二叉排序树如下图 （a），平衡二叉树的结构被破坏，此时只需要对二叉排序树做“旋转”操作（如下图 （b）），即整棵树以结点 24 为根结点，二叉排序树的结构没有破坏，同时将该树转化为了平衡二叉树：

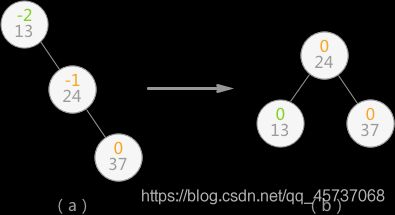
当二叉排序树的平衡性被打破时，就如同扁担的两头出现了一头重一头轻的现象，如下图（a）所示，此时只需要改变扁担的支撑点（树的树根），就能使其重新归为平衡。实际上图b中的 （b） 是对（a） 的二叉树做了一个向左逆时针旋转的操作。

继续插入 90 和 53 后，二叉排序树如下图（a）所示，导致二叉树中结点 24 和 37 的平衡因子的绝对值大于 1 ，整棵树的平衡被打破。此时，需要做两步操作：

1. 如下图（b） 所示，将结点 53 和 90 整体向右顺时针旋转，使本该以 90 为根结点的子树改为以结点 53 为根结点；
2. 如下图 （c） 所示，将以结点 37 为根结点的子树向左逆时针旋转，使本该以 37 为根结点的子树，改为以结点 53 为根结点；

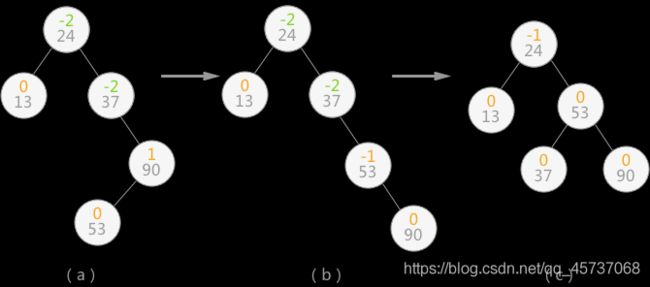做完以上操作，即完成了由不平衡的二叉排序树转变为平衡二叉树。

3.不平衡因子的四种情况

1.单向右旋平衡处理：若由于结点 a 的左子树为根结点的左子树上插入结点，导致结点 a 的平衡因子由 1 增至 2，致使以 a 为根结点的子树失去平衡，则只需进行一次向右的顺时针旋转，如下图这种情况：

2.单向左旋平衡处理：如果由于结点 a 的右子树为根结点的右子树上插入结点，导致结点 a 的平衡因子由 -1变为 -2，则以 a 为根结点的子树需要进行一次向左的逆时针旋转，如下图这种情况：

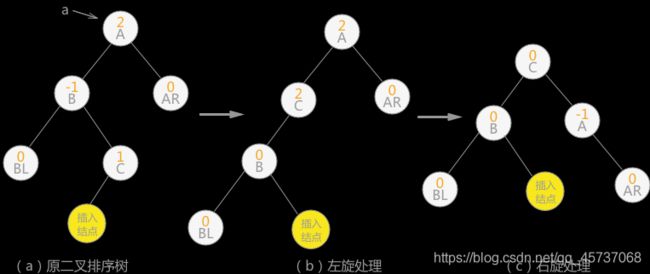
3.双向旋转（先左后右）平衡处理：如果由于结点 a 的左子树为根结点的右子树上插入结点，导致结点 a 平衡因子由 1 增至 2，致使以 a 为根结点的子树失去平衡，则需要进行两次旋转操作，如下图这种情况：

上图中插入结点也可以为结点 C 的右孩子，则（b）中插入结点的位置还是结点 C 右孩子，（c）中插入结点的位置为结点 A 的左孩子。

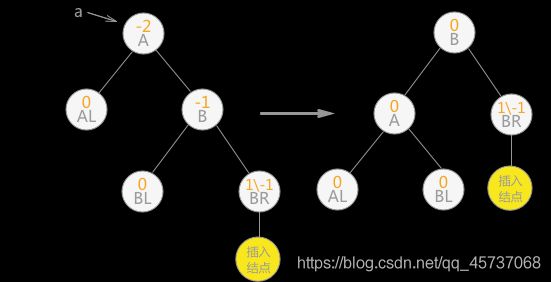
4.双向旋转（先右后左）平衡处理：如果由于结点 a 的右子树为根结点的左子树上插入结点，导致结点 a 平衡因子由 -1 变为 -2，致使以 a 为根结点的子树失去平衡，则需要进行两次旋转（先右旋后左旋）操作，如下图这种情况：

上图中插入结点也可以为结点 C 的右孩子，则（b）中插入结点的位置改为结点 B 的左孩子，（c）中插入结点的位置为结点 B 的左孩子

4.构建平衡二叉树的代码实现

#include 
#include 
//分别定义平衡因子数
#define LH +1
#define EH  0
#define RH -1
typedef int ElemType;
typedef enum {false,true} bool;
//定义二叉排序树
typedef struct BSTNode{
    ElemType data;
    int bf;//balance flag
    struct BSTNode *lchild,*rchild;
}*BSTree,BSTNode;
//对以 p 为根结点的二叉树做右旋处理，令 p 指针指向新的树根结点
void R_Rotate(BSTree* p)
{
    //借助文章中的图 5 所示加以理解，其中结点 A 为 p 指针指向的根结点
    BSTree lc = (*p)->lchild;
    (*p)->lchild = lc->rchild;
    lc->rchild = *p;
    *p = lc;
}
对以 p 为根结点的二叉树做左旋处理，令 p 指针指向新的树根结点
void L_Rotate(BSTree* p)
{
    //借助文章中的图 6 所示加以理解，其中结点 A 为 p 指针指向的根结点
    BSTree rc = (*p)->rchild;
    (*p)->rchild = rc->lchild;
    rc->lchild = *p;
    *p = rc;
}
//对以指针 T 所指向结点为根结点的二叉树作左子树的平衡处理，令指针 T 指向新的根结点
void LeftBalance(BSTree* T)
{
    BSTree lc,rd;
    lc = (*T)->lchild;
    //查看以 T 的左子树为根结点的子树，失去平衡的原因，如果 bf 值为 1 ，则说明添加在左子树为根结点的左子树中，需要对其进行右旋处理；反之，如果 bf 值为 -1，说明添加在以左子树为根结点的右子树中，需要进行双向先左旋后右旋的处理
    switch (lc->bf)
    {
        case LH:
            (*T)->bf = lc->bf = EH;
            R_Rotate(T);
            break;
        case RH:
            rd = lc->rchild;
            switch(rd->bf)
        {
            case LH:
                (*T)->bf = RH;
                lc->bf = EH;
                break;
            case EH:
                (*T)->bf = lc->bf = EH;
                break;
            case RH:
                (*T)->bf = EH;
                lc->bf = LH;
                break;
        }
            rd->bf = EH;
            L_Rotate(&(*T)->lchild);
            R_Rotate(T);
            break;
    }
}
//右子树的平衡处理同左子树的平衡处理完全类似
void RightBalance(BSTree* T)
{
    BSTree lc,rd;
    lc= (*T)->rchild;
    switch (lc->bf)
    {
        case RH:
            (*T)->bf = lc->bf = EH;
            L_Rotate(T);
            break;
        case LH:
            rd = lc->lchild;
            switch(rd->bf)
        {
            case LH:
                (*T)->bf = EH;
                lc->bf = RH;
                break;
            case EH:
                (*T)->bf = lc->bf = EH;
                break;
            case RH:
                (*T)->bf = EH;
                lc->bf = LH;
                break;
        }
            rd->bf = EH;
            R_Rotate(&(*T)->rchild);
            L_Rotate(T);
            break;
    }
}

int InsertAVL(BSTree* T,ElemType e,bool* taller)
{
    //如果本身为空树，则直接添加 e 为根结点
    if ((*T)==NULL)
    {
        (*T)=(BSTree)malloc(sizeof(BSTNode));
        (*T)->bf = EH;
        (*T)->data = e;
        (*T)->lchild = NULL;
        (*T)->rchild = NULL;
        *taller=true;
    }
    //如果二叉排序树中已经存在 e ，则不做任何处理
    else if (e == (*T)->data)
    {
        *taller = false;
        return 0;
    }
    //如果 e 小于结点 T 的数据域，则插入到 T 的左子树中
    else if (e < (*T)->data)
    {
        //如果插入过程，不会影响树本身的平衡，则直接结束
        if(!InsertAVL(&(*T)->lchild,e,taller))
            return 0;
        //判断插入过程是否会导致整棵树的深度 +1
        if(*taller)
        {
            //判断根结点 T 的平衡因子是多少，由于是在其左子树添加新结点的过程中导致失去平衡，所以当 T 结点的平衡因子本身为 1 时，需要进行左子树的平衡处理，否则更新树中各结点的平衡因子数
            switch ((*T)->bf)
            {
                case LH:
                    LeftBalance(T);
                    *taller = false;
                    break;
                case  EH:
                    (*T)->bf = LH;
                    *taller = true;
                    break;
                case RH:
                    (*T)->bf = EH;
                    *taller = false;
                    break;
            }
        }
    }
    //同样，当 e>T->data 时，需要插入到以 T 为根结点的树的右子树中，同样需要做和以上同样的操作
    else
    {
        if(!InsertAVL(&(*T)->rchild,e,taller))
            return 0;
        if (*taller)
        {
            switch ((*T)->bf)
            {
                case LH:
                    (*T)->bf = EH;
                    *taller = false;
                    break;
                case EH:
                    (*T)->bf = RH;
                    *taller = true;
                    break;
                case  RH:
                    RightBalance(T);
                    *taller = false;
                    break;
            }
        }
    }
    return 1;
}
//判断现有平衡二叉树中是否已经具有数据域为 e 的结点
bool FindNode(BSTree root,ElemType e,BSTree* pos)
{
    BSTree pt = root;
    (*pos) = NULL;
    while(pt)
    {
        if (pt->data == e)
        {
            //找到节点，pos指向该节点并返回true
            (*pos) = pt;
            return true;
        }
        else if (pt->data>e)
        {
            pt = pt->lchild;
        }
        else
            pt = pt->rchild;
    }
    return false;
}
//中序遍历平衡二叉树
void InorderTra(BSTree root)
{
    if(root->lchild)
        InorderTra(root->lchild);
   
    printf("%d ",root->data);
   
    if(root->rchild)
        InorderTra(root->rchild);
}

int main()
{
    int i,nArr[] = {1,23,45,34,98,9,4,35,23};
    BSTree root=NULL,pos;
    bool taller;
    //用 nArr查找表构建平衡二叉树（不断插入数据的过程）
    for (i=0;i<9;i++)
    {
        InsertAVL(&root,nArr[i],&taller);
    }
    //中序遍历输出
    InorderTra(root);
    //判断平衡二叉树中是否含有数据域为 103 的数据
    if(FindNode(root,103,&pos))
        printf("\n%d\n",pos->data);
    else
        printf("\nNot find this Node\n");
    return 0;
}