平衡树的调整 案例与代码

一,分析平衡二叉查找树有什么意义？

   平衡二叉查找树是对二叉查找树的改进，那二叉查找树哪些地方是不尽人意的呢？

在分析二叉查找树的平均查找长度时，会发现，二叉查找树的平均查找长度与二叉查找树

的形态有关系，最坏的情况是退化为链表，查找变为线性查找，平均查找长度为(n 1)/2.最

好的情况就是树的形态与折半查找的判断树形式。平均查找长度为logN。

平衡二叉树就是为了保证树的形态向“树”的方向走。避免了二叉查找树退化为链表的可能。

从而提高了查找效率。其实平衡二叉查找树与二叉查找树的区别并不是很大，平衡树在“改变”

树的时候会维护树的形态，“改变”无非就两种，插入节点和删除节点，而树的查找只“读”

了树，并没改变，所以树的查找，平衡树和查找树是一样的。

例如：

现在我要使用24,12,53,28,45,90创建查找树，如果创建的二叉查找树（如左图），

则平均查找长度：(1 2 2 3 4 3)/6 = 15/6 如果创建的是平衡二叉查找树(如右图)，

则平均查找长度：(2 3 2 3 1 3)/6 = 14/6. 平衡二叉树的查找效率要高，

这个例子是借用上次使用的，可能代表性不是强。

----------------------------------------------------------------

二，平衡二叉查找树相关的重要概念。

1，什么是平衡二叉查找树？

平衡二叉查找树又称为平衡二叉排序树，又称为AVL树，是二叉查找树的改进。
     定义（满足如下三个条件）：
           (1),是二叉查找树。
           (2),左子树与右子树的深度之差的绝对值小于或等于1.
           (3),左右子树也是平衡二叉查找树。 

2，什么是平衡因子？

平衡二叉查找树的每个结点都要描述一个属性，就是平衡因子，
      它表示结点的左子树深度与右子树深度之差。 

该概念的引入也是为了更好地描述什么是平衡二叉查找树。有了这概念后。

我们可以重新对二叉查找树下个定义。

如果某个二叉查找树的所有节点的平衡因子只有-1,0,1则说明其实平衡的，

否则说明是不平衡的。
-------------------------------------------------------------------
三，平衡二叉查找树是如何创建和插入的？如何保证插入一个新节点后树仍然是

一棵平衡二叉查找树？

先介绍几个特殊的节点。

插入一个新的节点，只有该节点的祖先节点的平衡因子会变化，其他节点的

平衡因子都不会变化。

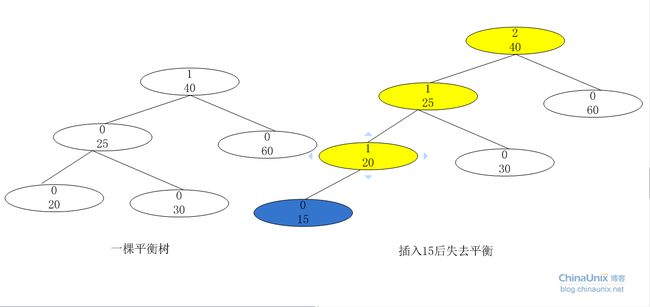
如上图，插入15这个节点后，平衡因子变化的只有20,25,40。都是15的“祖先节点”。

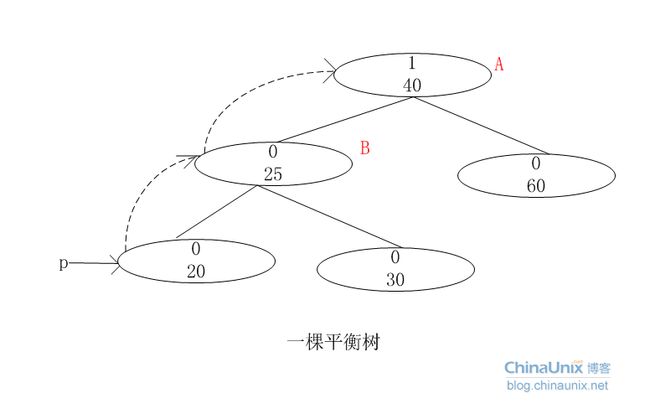
A节点：为插入点最底层“祖先节点”最可能的失衡点。比如插入的节点是15，故插入的位置是节点20的左孩子，这从20这个节点开始遍历祖先节点，取最近的的最可能失衡点，
这儿就是40这个节点。如果没有找到，说明插入这个节点不可能破坏平衡
B节点就是该祖先节点一条线中A节点的下一个。

这两个特殊的点很重要，因为后面的失衡类型就是根据这两个点的平衡因子来判断的。

插入节点很简单，主要就是插入节点后有可能破坏平衡，那就必须将非平衡的树调整为平衡树。

现在将非平衡的情况分为四种，每种情况都有自己的调整方法。

1，LL型。（左边重，需往右边转）

LL型的判断依据就是:A节点平衡因子为2，B节点的平衡因子为1.

即: A->bf = 2, B->bf = 1.

如果失衡类型是LL型，这调整算法如下：

以B点为轴，将A节点做顺时针旋转，然后将B的右子树作为A的左子树。

算法的代码实现如下：（可结合上面的图看）

case LL:
            B = A->lchild;//该类型B节点所在的位置
            A->lchild = B->rchild;//将B节点的右子树交给A，作为A的左子树。
            B->rchild = A;//把A作为B的右子树。
            A->bf = B->bf = 0;//更新A，B节点的平衡因子的值。
            if (father_A == NULL)  *root = B;//如果A是根，则现在把B节点设置为根节点。
            else if (A  == father_A->lchild) father_A->lchild = B;//如果原来A是father_A的
//左孩子，则现在把B，作为father_A的左孩子。否则，作为father_A的右孩子，就是用B的取代A原来的位置。
            else    father_A->rchild = B;
            break;

该算法的过程实现起来并不难，主要还是有人家的理论在这儿放着。详细的过程看代码注释。

2，RR型。与LL型是对称的。（右边重，需往左边转）

RR型的判断依据就是:A节点平衡因子为-2，B节点的平衡因子为-1.

即: A->bf = -2, B->bf = -1.

如果失衡类型是RR型，这调整算法如下：

该类型的调整和LL型调整差不多。以B节点为轴，将A节点作逆时针旋转，然后，把B的

左子树给A，作为A的右子树。

算法的代码实现如下：

case RR:
    B = A->rchild;//该类型B节点所在的位置
    A->rchild = B->lchild;//把B的左子树给A，充当A的右子树。
    B->lchild = A;//将A充当B的左子树，完成了逆时针旋转。
    A->bf = B->bf = 0;//重新设置平衡因子。
    if  (father_A == NULL)  *root = B;//看原来A在整个树中的位置，现在将B取代A的位置
    else  if (A == father_A->lchild) father_A->lchild = B;
    else father_A->rchild = B;
    break;

该类型和LL型是对称的，只要理解了其中一个，另外一个很好理解。

3，LR型。（左边，右边都重，都需要转）

该类型又引入了一个特殊节点C。该节点很好判断，和判断B节点一样，插入节点的

“祖先节点”那一线上，A的下一个是B，B的下一个就是C节点。

LR型的判断依据就是:A节点平衡因子为2，B节点的平衡因子为-1.

即: A->bf = 2, B->bf = -1.

如果失衡类型是LR型，这调整算法如下：

算法的实现代码分析：

case LR:
            B = A->lchild;//该类型B节点的位置
            C = B->rchild;//该类型C节点的位置
            B->rchild = C->lchild;//C节点的左子树交给B，作为B的右子树。
            A->lchild = C->rchild;//C节点的右子树交给A，作为A的左子树。
            C->lchild = B;//B作为C的左子树
            C->rchild = A;//A作为A的右子树
            if (s->key < C->key) {//根据插入节点与C节点的位置来更新平衡因子的值
                A->bf = -1;B->bf = 0;C->bf = 0;
            } else if  (s->key > C->key) {
                A->bf =0;B->bf = 1;C->bf = 0;
            } else {
                A->bf = 0;B->bf = 0;
            }
            if (father_A == NULL)  *root = C;//用C节点来取代A节点的位置。
            else if (A  == father_A->lchild) father_A->lchild = C;
            else father_A->rchild = C;
            break;

该类型的调整算法见代码注释。

4，RL型。（左边，右边都重，都需要转）
      这种类型和LR型是对称的，分析起来思路是一样的。故不再详细分析。

--------------------------------------------------------------------------------------
四，平衡树节点的删除，平衡树节点的删除和插入差不多，都有可能导致

平衡树的失衡，在删除节点后同样要找到A点和B点，然后判断是否有失衡，

如果失衡了，然后根据失衡的类型作出调整。调整的算法见上面的分析。