微积分的总结
再学微积分
初入微积分:不定积分
定义:不定积分是求导运算和微分运算不完全的逆运算。也是一种非构造的运算。
- 为什么是它是它的逆运算?
- 为什么说是不完全的逆运算?
- 为什么说它是非构造的运算?
F ′ ( x ) = f ( x ) d F ( x ) = f ( x ) d x ∫ f ( x ) d x = F ( x ) + C F'(x)=f(x)\\ dF(x)=f(x)dx\\ \int f(x)dx=F(x)+C F′(x)=f(x)dF(x)=f(x)dx∫f(x)dx=F(x)+C
所以,称它是它的逆运算。
证 明 : 为 什 么 f ( x ) 的 原 函 数 是 且 仅 是 F ( x ) + C ? 证明:为什么f(x)的原函数是且仅是F(x)+C? 证明:为什么f(x)的原函数是且仅是F(x)+C?
假 设 f ( x ) 的 原 函 数 不 止 一 个 , 设 F ( x ) 是 其 中 的 特 定 的 某 一 个 。 假设f(x)的原函数不止一个,设F(x)是其中的特定的某一个。 假设f(x)的原函数不止一个,设F(x)是其中的特定的某一个。
G ( x ) 代 表 其 中 的 任 意 一 个 。 则 , 根 据 原 函 数 的 定 义 , 有 : G(x)代表其中的任意一个。则,根据原函数的定义,有: G(x)代表其中的任意一个。则,根据原函数的定义,有:
F ′ ( x ) = f ( x ) , 且 G ′ ( x ) = f ( x ) , 则 有 : h ( x ) = G ′ ( x ) − F ′ ( x ) = 0 。 F'(x)=f(x),且G'(x)=f(x),则有:h(x)=G'(x)-F'(x)=0。 F′(x)=f(x),且G′(x)=f(x),则有:h(x)=G′(x)−F′(x)=0。
所 以 , 只 要 F ( x ) 是 f ( x ) 的 一 个 原 函 数 , 任 意 的 一 个 原 函 数 都 可 以 被 表 示 为 : 所以,只要F(x)是f(x)的一个原函数,任意的一个原函数都可以被表示为: 所以,只要F(x)是f(x)的一个原函数,任意的一个原函数都可以被表示为:
F ( x ) + C , 所 以 f ( x ) 的 原 函 数 是 且 仅 是 F ( x ) + C F(x)+C,所以f(x)的原函数是且仅是F(x)+C F(x)+C,所以f(x)的原函数是且仅是F(x)+C
假设不定积分和求导,微分在两个空间之间建立起了联系,那么,假设运算从求导,微分开始:
解空间 C 1 C1 C1对应的解空间 C 2 C2 C2所对应的解空间不是 C 1 C1 C1。实际上 C 2 C2 C2是 C 1 C1 C1的父集。
故称它们是一对不完全的逆运算。
任何一个特定的不定积分的求解空间 Y 2 Y2 Y2是所有不定积分的求解空间的合空间 Y 1 Y1 Y1的一个很小的子集。
所以说它是非构造的运算。
基本的不定积分公式
∫ 0 d x = C ∫ 1 d x = ∫ d x = x + C ∫ x a d x = 1 a + 1 x a + 1 + C ( a ≠ − 1 ) ∫ x − 1 d x = l n ∣ x ∣ + C ∫ a x d x = a x l n a + C ∫ e x d x = e x + C ∫ c o s x d x = s i n x + C ∫ s i n x d x = − c o s x + C ∫ s e c 2 x d x = t a n x + C ∫ c s c 2 d x = − c o t x + C ∫ s e c x t a n x d x = s e c x + C ∫ c s c x c o t x d x = − c s c x + C ∫ 1 1 + x 2 d x = a r c t a n x + C = − a r c c o t x + C 1 ∫ 1 1 − x 2 d x = a r c s i n x + C = − a r c c o s x + C 1 \int 0dx=C\\ \int 1dx=\int d x=x+C \\ \int x^adx=\frac{1}{a+1}x^{a+1}+C (a\not =-1)\\ \int x^{-1}dx= ln |x|+C\\ \int a^x dx= \frac{a^x}{ln a}+C\\ \int e^xdx= e^x+C\\ \int cos xdx= sin x+C\\ \int sin xdx= -cos x+C\\ \int sec^2xdx= tanx +C\\ \int csc^2dx= -cot x+C\\ \int sec x tan xdx=sec x +C\\ \int csc x cot xdx=-csc x +C\\ \int \frac{1}{1+x^2}dx= arctan x+C=-arccot x+C1\\ \int \frac{1}{\sqrt{1-x^2}}dx=arcsin x +C=-arccos x+C1 ∫0dx=C∫1dx=∫dx=x+C∫xadx=a+11xa+1+C(a=−1)∫x−1dx=ln∣x∣+C∫axdx=lnaax+C∫exdx=ex+C∫cosxdx=sinx+C∫sinxdx=−cosx+C∫sec2xdx=tanx+C∫csc2dx=−cotx+C∫secxtanxdx=secx+C∫cscxcotxdx=−cscx+C∫1+x21dx=arctanx+C=−arccotx+C1∫1−x21dx=arcsinx+C=−arccosx+C1
不定积分的四大法宝
1. 不定积分的线性运算法则
若 ∫ f ( x ) d x , ∫ g ( x ) d x 均 存 在 ∀ α , β ( 不 同 时 为 零 ) 则 : ∫ [ α f ( x ) + β g ( x ) ] d x = α ∫ f ( x ) d x + β ∫ g ( x ) d x 若\int f(x)dx,\int g(x)dx均存在\\ {\forall}\alpha,\beta(不同时为零)\\ 则:\int[\alpha f(x)+\beta g(x)]dx=\alpha \int f(x)dx+\beta \int g(x)dx 若∫f(x)dx,∫g(x)dx均存在∀α,β(不同时为零)则:∫[αf(x)+βg(x)]dx=α∫f(x)dx+β∫g(x)dx
例题1
求 ∫ t a n 2 x d x ∫ t a n 2 x d x = ∫ ( s e c 2 x − 1 ) d x = ∫ s e c 2 x d x − ∫ d x 求\int tan^2xdx\\ \int tan^2xdx=\int (sec^2x-1)dx=\int sec^2 xdx-\int dx 求∫tan2xdx∫tan2xdx=∫(sec2x−1)dx=∫sec2xdx−∫dx
例题2
求 ∫ 1 s i n 2 x c o s 2 ∫ 1 s i n 2 x c o s 2 = ∫ s i n 2 x + c o s 2 s i n 2 x c o s 2 = ∫ ( s e c 2 x + c s c 2 x ) d x 求\int \frac{1}{sin^2xcos^2}\\ \int \frac{1}{sin^2xcos^2}=\int \frac{sin^2x+cos^2}{sin^2xcos^2}=\int (sec^2x+csc^2x)dx 求∫sin2xcos21∫sin2xcos21=∫sin2xcos2sin2x+cos2=∫(sec2x+csc2x)dx
例题3
求 ∫ x 4 x 2 + 1 d x ∫ x 4 x 2 + 1 d x = ∫ x 4 − 1 + 1 x 2 + 1 d x = ∫ ( x 2 − 1 + 1 x 2 + 1 ) d x 求\int \frac{x^4}{x^2+1}dx\\ \int \frac{x^4}{x^2+1}dx=\int \frac{x^4-1+1}{x^2+1}dx=\int (x^2-1+\frac{1}{x^2+1})dx 求∫x2+1x4dx∫x2+1x4dx=∫x2+1x4−1+1dx=∫(x2−1+x2+11)dx
2. 不定积分的凑微分(第一换元法)
定义:在保持被积表达式的值不变时,于内部进行微分运算,以同时改变被积函数和积分变量,在整体上达到被积表达式形式的改变,以使其形式更加便于求解。
例题1
求 ∫ t a n x d x ∫ t a n x d x = − ∫ 1 c o s x d c o s x = − l n ∣ c o s x ∣ + C ( ∫ c o t x d x = l n ∣ s i n x ∣ + C ) 求\int tan xdx\\ \int tan xdx=-\int \frac{1}{cos x}dcosx =-ln|cosx|+C\\ (\int cot x dx=ln|sinx|+C) 求∫tanxdx∫tanxdx=−∫cosx1dcosx=−ln∣cosx∣+C(∫cotxdx=ln∣sinx∣+C)
记住一些微分关系式
a ∗ d x = d ( a x + b ) 2 x ∗ d x = d ( x 2 ± a 2 ) − 2 x ∗ d x = d ( a 2 − x 2 ) c o s x d x = d s i n x s i n x d x = − d c o s x 1 x d x = d ∣ l n x ∣ e x d x = d e x a*dx=d(ax+b)\\ 2x*dx=d(x^2 \pm a^2)\\ -2x*dx=d(a^2 - x^2)\\ cos xdx=dsinx\\ sinxdx=-dcosx\\ \frac{1}{x}dx=d|lnx|\\ e^xdx=de^x a∗dx=d(ax+b)2x∗dx=d(x2±a2)−2x∗dx=d(a2−x2)cosxdx=dsinxsinxdx=−dcosxx1dx=d∣lnx∣exdx=dex
例题2
求 ∫ 1 a 2 + x 2 d x ( a ≠ 0 ) ∫ 1 a 2 + x 2 d x = 1 a 2 ∫ 1 1 + ( x a ) 2 d x = 1 a ∫ 1 1 + ( x a ) 2 d ( x a ) = 1 a a r c t a n x a + C 求\int \frac{1}{a^2+x^2}dx(a \not =0)\\ \int \frac{1}{a^2+x^2}dx=\frac{1}{a^2}\int \frac{1}{1+(\frac{x}{a})^2}dx=\frac{1}{a}\int \frac{1}{1+(\frac{x}{a})^2}d(\frac{x}{a})\\ =\frac{1}{a}arctan \frac{x}{a}+C 求∫a2+x21dx(a=0)∫a2+x21dx=a21∫1+(ax)21dx=a1∫1+(ax)21d(ax)=a1arctanax+C
例题3
求 ∫ 1 a 2 − x 2 d x ( a > 0 ) ∫ 1 a 2 − x 2 d x = 1 a ∫ 1 1 − ( x a ) 2 d x = ∫ 1 1 − ( x a ) 2 d ( x a ) = a r c s i n x a + C 求\int \frac{1}{\sqrt{a^2-x^2}}dx(a>0)\\ \int \frac{1}{\sqrt{a^2-x^2}}dx=\frac{1}{a}\int \frac{1}{\sqrt{1-(\frac{x}{a})^2}}dx=\int \frac{1}{\sqrt{1-(\frac{x}{a})^2}}d(\frac{x}{a})\\ =arcsin \frac{x}{a}+C 求∫a2−x21dx(a>0)∫a2−x21dx=a1∫1−(ax)21dx=∫1−(ax)21d(ax)=arcsinax+C
例题4
求 ∫ 1 a 2 − x 2 d x ( a ≠ 0 ) ∫ 1 a 2 − x 2 d x ( a ≠ 0 ) = ∫ 1 ( a − x ) ( a + x ) d x = 1 2 a ∫ ( 1 a − x − 1 a + x ) d x = 1 2 a ∫ ( 1 a − x − 1 a + x ) d x = 1 2 a [ ∫ 1 a − x d x − ∫ 1 a + x d x ] = 1 2 a l n ∣ a + x a − x ∣ + C 求\int \frac{1}{a^2-x^2}dx(a \not =0)\\ \int \frac{1}{a^2-x^2}dx(a \not =0)=\int \frac{1}{(a-x)(a+x)}dx=\frac{1}{2a}\int (\frac{1}{a-x}-\frac{1}{a+x})dx\\=\frac{1}{2a}\int (\frac{1}{a-x}-\frac{1}{a+x})dx=\frac{1}{2a}[\int \frac{1}{a-x}dx- \int \frac{1}{a+x}dx] \\ =\frac{1}{2a}ln|\frac{a+x}{a-x}| +C 求∫a2−x21dx(a=0)∫a2−x21dx(a=0)=∫(a−x)(a+x)1dx=2a1∫(a−x1−a+x1)dx=2a1∫(a−x1−a+x1)dx=2a1[∫a−x1dx−∫a+x1dx]=2a1ln∣a−xa+x∣+C
例题5
求 ∫ s e c x d x ∫ s e c x d x = ∫ 1 1 − s i n x 2 d s i n x = l n ∣ s e c x + t a n x ∣ + C ( ∫ c s c x d x = l n ∣ c s c x − c o t x ∣ + C ) 求\int secxdx\\ \int secx dx=\int \frac{1}{1-sinx^2}dsinx\\ =ln|secx+tanx|+C\\ (\int csc x dx=ln|cscx-cotx|+C) 求∫secxdx∫secxdx=∫1−sinx21dsinx=ln∣secx+tanx∣+C(∫cscxdx=ln∣cscx−cotx∣+C)
另解:
求 ∫ s e c x d x ∫ s e c x d x = ∫ s e c x ( s e c x + t a n x ) s e c x + t a n x d x = ∫ 1 s e c x + t a n x d ( s e c x + t a n x ) = l n ∣ s e c x + t a n x ∣ + C 求\int secxdx\\ \int secxdx=\int \frac{secx(secx+tanx)}{secx+tanx}dx=\int \frac{1}{secx+tanx}d(secx+tanx)\\ =ln|secx+tanx|+C 求∫secxdx∫secxdx=∫secx+tanxsecx(secx+tanx)dx=∫secx+tanx1d(secx+tanx)=ln∣secx+tanx∣+C
例题6
求 ∫ e a x ∫ e a x = 1 a ∫ e a x d ( a x ) = 1 a e a x + C ( ∫ c o s a x d x = 1 a s i n a x + C ) ( ∫ s i n a x d x = − 1 a c o s a x + C ) 求\int e^{ax}\\ \int e^{ax}=\frac{1}{a}\int e^{ax}d(ax)\\ =\frac{1}{a}e^{ax}+C\\ (\int cosaxdx=\frac{1}{a}sinax+C)\\ (\int sinaxdx=-\frac{1}{a}cosax+C) 求∫eax∫eax=a1∫eaxd(ax)=a1eax+C(∫cosaxdx=a1sinax+C)(∫sinaxdx=−a1cosax+C)
3. 不定积分的变量代换(第二换元法)
定义:创建一个新的变元,并使其与x建立函数关系(这个函数被要求是可导并且严格单调的),而代替入被积表达式之中,以此使得被积表达式的形式发生变化,以使其形式更加便于求解
记忆一些常用的代换
- a 2 − x 2 , 令 x = a s i n t , t ∈ [ − π 2 , π 2 ] \sqrt{a^2-x^2} ,令x=asint,t \in [-\frac{\pi}{2},\frac{\pi}{2}] a2−x2,令x=asint,t∈[−2π,2π]
- a 2 + x 2 , 令 x = a t a n t , t ∈ [ − π 2 , π 2 ] \sqrt{a^2+x^2} ,令x=atant,t \in [-\frac{\pi}{2},\frac{\pi}{2}] a2+x2,令x=atant,t∈[−2π,2π]
- x 2 − a 2 , 令 x = a s e c t , t ∈ [ 0 , π 2 ] ∪ [ π 2 , π ] \sqrt{x^2-a^2} ,令x=asect,t \in [0,\frac{\pi}{2}]\cup [\frac{\pi}{2},\pi] x2−a2,令x=asect,t∈[0,2π]∪[2π,π]
- a x + b c x + d n , 令 a x + b c x + d n = t \sqrt[n]{\frac{ax+b}{cx+d}} ,令\sqrt[n]{\frac{ax+b}{cx+d}}=t ncx+dax+b,令ncx+dax+b=t
- a x + b n , 令 a x + b n = t \sqrt[n]{ax+b} ,令\sqrt[n]{ax+b}=t nax+b,令nax+b=t
例题1
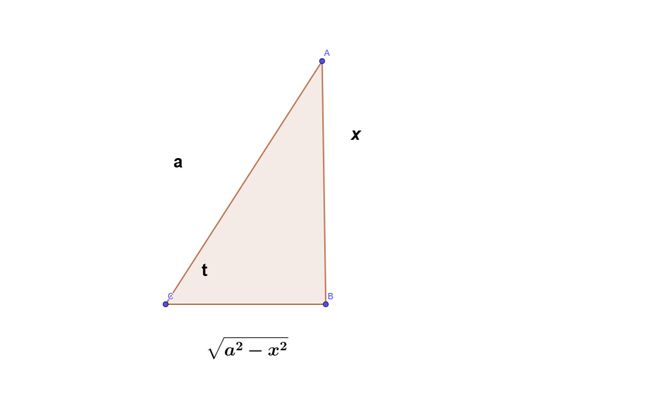
求 ∫ a 2 − x 2 d x 令 x = a s i n t ∫ a 2 − x 2 = ∫ a 2 − a 2 s i n 2 t a c o s t d t = a 2 ∫ ∣ c o s t ∣ c o s t d t = a 2 ∫ c o s 2 t d t = a 2 2 ∫ ( 1 + c o s 2 t ) t d t = a 2 2 t + a 2 4 s i n 2 t + C = a 2 2 a r c s i n x a + a 2 2 s i n t c o s t + C 求\int \sqrt{a^2-x^2}dx\\ 令x=asint\\ \int \sqrt{a^2-x^2}=\int \sqrt{a^2-a^2sin^2t} acost dt=a^2\int |cost|costdt \\ =a^2\int cos^2tdt=\frac{a^2}{2}\int (1+cos2t)tdt=\frac{a^2}{2}t+\frac{a^2}{4}sin2t+C\\ =\frac{a^2}{2}arcsin \frac{x}{a}+ \frac{a^2}{2}sintcost+C 求∫a2−x2dx令x=asint∫a2−x2=∫a2−a2sin2tacostdt=a2∫∣cost∣costdt=a2∫cos2tdt=2a2∫(1+cos2t)tdt=2a2t+4a2sin2t+C=2a2arcsinax+2a2sintcost+C
再 根 据 上 面 的 三 角 形 法 则 , = a 2 2 a r c s i n x a + a 2 2 ∗ x a a 2 − x 2 a + C = a 2 2 ∗ 1 2 x a 2 − x 2 + C 再根据上面的三角形法则,\\ =\frac{a^2}{2}arcsin \frac{x}{a}+ \frac{a^2}{2}* \frac{x}{a} \frac{\sqrt{a^2-x^2}}{a}+C=\frac{a^2}{2}* \frac{1}{2}x\sqrt{a^2-x^2}+C 再根据上面的三角形法则,=2a2arcsinax+2a2∗axaa2−x2+C=2a2∗21xa2−x2+C
例题2
求 ∫ 1 x 2 + a 2 d x ( a > 0 ) 令 x = a t a n t ∫ 1 x 2 + a 2 d x = ∫ a s e c 2 a 2 t a n 2 t + a 2 d t = ∫ s e c t d t = l n ∣ s e c t + t a n t ∣ + C 再 次 运 用 三 角 形 法 则 。 此 处 省 略 。 = l n ∣ x + x 2 + a 2 ∣ + C ( 同 理 : ∫ 1 x 2 − a 2 d x = l n ∣ x + x 2 − a 2 ∣ + C ) ( 涉 及 到 绝 对 值 问 题 ) 求\int \frac{1}{\sqrt{x^2+a^2}}dx(a>0)\\ 令x=atant\\ \int \frac{1}{\sqrt{x^2+a^2}}dx=\int \frac{asec^2}{a^2tan^2t+a^2}dt\\ =\int sectdt=ln|sect+tant|+C\\ 再次运用三角形法则。此处省略。\\ =ln|x+ \sqrt{x^2+a^2}|+C\\ (同理:\int \frac{1}{\sqrt{x^2-a^2}}dx=ln|x+ \sqrt{x^2-a^2}|+C)(涉及到绝对值问题) 求∫x2+a21dx(a>0)令x=atant∫x2+a21dx=∫a2tan2t+a2asec2dt=∫sectdt=ln∣sect+tant∣+C再次运用三角形法则。此处省略。=ln∣x+x2+a2∣+C(同理:∫x2−a21dx=ln∣x+x2−a2∣+C)(涉及到绝对值问题)
例题3
求 ∫ 1 x + x 3 d x 令 x 6 = t ∫ 1 x + x 3 d x = ∫ 6 t 5 t 3 + t 2 d t = 6 ∫ t 3 + 1 − 1 t + 1 d t = 6 ∫ ( t 2 − t + 1 + 1 t + 1 ) d x = 6 ( 1 3 t 3 − 1 2 t 2 − l n ( 1 + t ) ) + C = . . . 求\int \frac{1}{\sqrt{x}+\sqrt[3]{x}}dx\\ 令 \sqrt[6]{x}=t\\ \int \frac{1}{\sqrt{x}+\sqrt[3]{x}}dx=\int \frac{6t^5}{t^3+t^2}dt=6 \int \frac{t^3+1-1}{t+1}dt\\ =6 \int (t^2-t+1+ \frac{1}{t+1})dx=6(\frac{1}{3}t^3-\frac{1}{2}t^2-ln(1+t))+C=... 求∫x+3x1dx令6x=t∫x+3x1dx=∫t3+t26t5dt=6∫t+1t3+1−1dt=6∫(t2−t+1+t+11)dx=6(31t3−21t2−ln(1+t))+C=...
例题4
求 ∫ x 2 ( 2 x + 1 ) 10 d x 令 ( 2 x + 1 ) = t ∫ x 2 ( 2 x + 1 ) 10 d x = 1 8 ∫ t 2 − 2 t + 1 t 1 0 = . . . 求\int \frac{x^2}{(2x+1)^{10}}dx\\ 令(2x+1)=t\\ \int \frac{x^2}{(2x+1)^{10}}dx=\frac{1}{8}\int \frac{t^2-2t+1}{t^10}=... 求∫(2x+1)10x2dx令(2x+1)=t∫(2x+1)10x2dx=81∫t10t2−2t+1=...
3. 分部积分
定义:将被积函数分为相乘的两个部分, C 1 ( x ) C1(x) C1(x)和 C 2 ( x ) C2(x) C2(x)。对其中容易求导的一个求导,容易求原函数的求原函数,设其分别为 L 1 ( x ) L1(x) L1(x)和 L 2 ( x ) L2(x) L2(x)。将被积函数化为 g ( x ) = L 1 ( x ) × L 2 ( x ) d x g(x)=L1(x)\times L2(x)dx g(x)=L1(x)×L2(x)dx,有 ∫ f ( x ) d x + ∫ g ( x ) d x = C 1 ( x ) × L 2 ( x ) d x \int f(x)dx+\int g(x)dx=C1(x)\times L2(x)dx ∫f(x)dx+∫g(x)dx=C1(x)×L2(x)dx,编成一句口诀就是:“求原的真的求原了,求导的并不是真的求导”。
原 理 : ∫ u d v = u v − ∫ v d u 原理:\int udv=uv-\int vdu 原理:∫udv=uv−∫vdu
证明:
( u v ) ′ = u ′ v + u v ′ ∫ ( u v ) ′ d x = ∫ u ′ v d x + ∫ u v ′ d x u v = ∫ v d u + ∫ u d v ( 也 可 以 使 用 微 分 证 明 ) (uv)'=u'v+uv'\\ \int (uv)'dx=\int u'vdx+\int uv'dx\\ uv=\int vdu+\int udv\\ (也可以使用微分证明) (uv)′=u′v+uv′∫(uv)′dx=∫u′vdx+∫uv′dxuv=∫vdu+∫udv(也可以使用微分证明)
例题1
求 ∫ x e x d x ∫ x e x d x + ∫ e x d x = x e x ∫ x e x d x = x e x − e x + C 求\int xe^xdx\\ \int xe^xdx+\int e^xdx=xe^x\\ \int xe^xdx=xe^x-e^x+C 求∫xexdx∫xexdx+∫exdx=xex∫xexdx=xex−ex+C
记忆一些常见的分步积分情况
- L 1 ( x ) = P k ( x ) , L 2 ( x ) = e a x ( 需 要 k 次 不 定 积 分 ) L1(x)=P_k(x),L2(x)=e^{ax}(需要k次不定积分) L1(x)=Pk(x),L2(x)=eax(需要k次不定积分)
- L 1 ( x ) = P k ( x ) , L 2 ( x ) = c o s a x ( 需 要 k 次 不 定 积 分 ) L1(x)=P_k(x),L2(x)=cosax(需要k次不定积分) L1(x)=Pk(x),L2(x)=cosax(需要k次不定积分)
- L 1 ( x ) = P k ( x ) , L 2 ( x ) = s i n a x ( 需 要 k 次 不 定 积 分 ) L1(x)=P_k(x),L2(x)=sinax(需要k次不定积分) L1(x)=Pk(x),L2(x)=sinax(需要k次不定积分)
- L 1 ( x ) = h ( a r c . . . x ) , L 2 ( x ) = P ( x ) ( 能 凑 出 d a r c . . . x 则 先 凑 ) L1(x)=h(arc...x),L2(x)=P(x)(能凑出darc...x则先凑) L1(x)=h(arc...x),L2(x)=P(x)(能凑出darc...x则先凑)
- L 1 ( x ) = h ( l n x ) , L 2 ( x ) = P ( x ) ( 能 凑 出 d l n x 则 先 凑 ) L1(x)=h(lnx),L2(x)=P(x)(能凑出dlnx则先凑) L1(x)=h(lnx),L2(x)=P(x)(能凑出dlnx则先凑)
例题2
求 ∫ ( 1 + x 2 ) c o s 2 x d x ∫ ( 1 + x 2 ) c o s 2 x d x + ∫ ( 2 x ) ( s i n 2 x 2 ) = ( 1 + x 2 ) ( s i n 2 x 2 ) ∫ x s i n x + ∫ 1 ∗ ( − c o s x ) = x ( − c o s x ) 求\int (1+x^2)cos2xdx\\ \int (1+x^2)cos2xdx+\int (2x)( \frac{sin2x}{2})=(1+x^2)( \frac{sin2x}{2})\\ \int xsinx+\int1*(-cosx)=x(-cosx)\\ 求∫(1+x2)cos2xdx∫(1+x2)cos2xdx+∫(2x)(2sin2x)=(1+x2)(2sin2x)∫xsinx+∫1∗(−cosx)=x(−cosx)
例题3
求 ∫ a r c t a n x 1 + x 2 d x ∫ a r c t a n x 1 + x 2 d x = ∫ a r c t a n x d a r c t a n x = 1 2 ( a r c t a n x ) 2 + C 求\int \frac{arctanx}{1+x^2}dx\\ \int \frac{arctanx}{1+x^2}dx=\int arctanxdarctanx\\ =\frac{1}{2}(arctanx)^2+C 求∫1+x2arctanxdx∫1+x2arctanxdx=∫arctanxdarctanx=21(arctanx)2+C
例题4
求 ∫ a r c t a n x d x ∫ a r c t a n x d x + ∫ x ( 1 1 + x 2 ) = x a r c t a n x ∫ a r c t a n x d x = x a r c t a n x − 1 2 l n ( 1 + x 2 ) + C 求\int arctan xdx\\ \int arctan xdx+\int x(\frac{1}{1+x^2})=xarctanx\\ \int arctan xdx=xarctanx-\frac{1}{2}ln(1+x^2)+C 求∫arctanxdx∫arctanxdx+∫x(1+x21)=xarctanx∫arctanxdx=xarctanx−21ln(1+x2)+C
例题
求 ∫ a r c t a n x x 2 ( 1 + x 2 ) d x ∫ a r c t a n x x 2 ( 1 + x 2 ) d x = ∫ ( 1 x 2 − 1 1 + x 2 ) a r c t a n x d x = ∫ ( 1 x 2 ) a r c t a n x d x − ∫ a r c t a n x 1 + x 2 d x { ∫ ( 1 x 2 ) a r c t a n x d x + ∫ ( − 1 x ) ( 1 1 + x 2 ) = ( − 1 x ) a r c t a n x ∫ a r c t a n x 1 + x 2 d x = ∫ a r c t a n x d a r c t a n x 且 又 有 : ∫ ( 1 x ) ( 1 1 + x 2 ) d x = ∫ ( 1 x − x 1 + x 2 ) d x ∫ a r c t a n x x 2 ( 1 + x 2 ) d x = . . . 求\int \frac{arctanx}{x^2(1+x^2)}dx\\ \int \frac{arctanx}{x^2(1+x^2)dx}=\int (\frac{1}{x^2}-\frac{1}{1+x^2})arctanxdx\\ =\int (\frac{1}{x^2})arctanxdx-\int \frac{arctanx}{1+x^2}dx\\ \begin{cases} \int (\frac{1}{x^2})arctanxdx+\int (-\frac{1}{x})(\frac{1}{1+x^2})=(-\frac{1}{x})arctanx \\ \int \frac{arctanx}{1+x^2}dx=\int arctanxdarctanx \end{cases}\\ 且又有:\int (\frac{1}{x})(\frac{1}{1+x^2})dx=\int (\frac{1}{x}-\frac{x}{1+x^2})dx\\ \int \frac{arctanx}{x^2(1+x^2)}dx=... 求∫x2(1+x2)arctanxdx∫x2(1+x2)dxarctanx=∫(x21−1+x21)arctanxdx=∫(x21)arctanxdx−∫1+x2arctanxdx{∫(x21)arctanxdx+∫(−x1)(1+x21)=(−x1)arctanx∫1+x2arctanxdx=∫arctanxdarctanx且又有:∫(x1)(1+x21)dx=∫(x1−1+x2x)dx∫x2(1+x2)arctanxdx=...