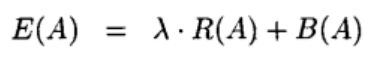经典图割算法中图的构建及实现:Graph-Cut

经典图割算法中图的构建及实现之graph-cut

本文目的：

讲解目前典型的3种图割算法：graph-cut、grab-but、one-cut。本文主要讲解graph-cut的方法在应用时，准则函数与图构建关系，如何构建图，以及如何代码实现图的构建。图割的原理网上文章和论文已介绍比较详细，不再详细介绍。

一．graph-cut：准则函数

该方法可谓是图割方法的开山鼻祖。该方法的准则函数如下：

R(A)是先验惩罚项，B(A)是区域相似度惩罚项，是平衡因子。

该准则函数意义：同类间，颜色差别小；异类间，颜色差别大。原则上该准则可解决图像任意类分割，并且一定是有全局最优解得，但在无种子点的超过2分类的问题时，该优化是个NP难问题，需要进行指数级的比较才能获得最优解，无工程价值。

二．Graph-cut：图的建立

1.术语：

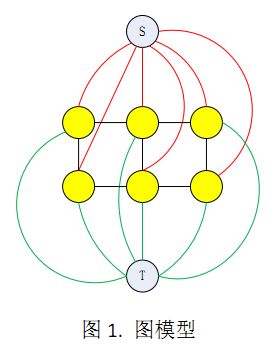
1. )与S和T链接的边叫t-link(红线与绿线)，领域之间的链接边叫n-link(黑线)。其中红线进一步称为s-t-link，绿线进一步称为t-t-link。
2. )黑线的权值对应的是B(A)项，红线与绿线的权值对应的是R(A)项。
3. )权值用w表示。
4. )蓝色节点表示类别标志节点，S表示正类类标节点，T表示负类类标节点，黄色节点是图像中的每一个像素点。

       最终通过求最小割之后，与节点S相连的所有黄色节点(图像像素点)属于一类，同理与节点T相连的所有黄色节点属于另一类。两类被最小割割开，割值即是准则函数的值。

2.图的建立

       拿到待分割的图像后，图的节点与边已确定，即图的形状已确定下来。仅仅需要做的就是给图中所有边赋值相应的权值。

图中的边有3种情况：种子点的t-link；非种子点的t-link；像素领域关系的n-link。接下来将说明每一种边的权值取值。

1).种子点t-link权值：种子点认为是硬约束，其用户预设类别后，类别不会随分割算法而改变。

a.对于正类别种子点，s-t-link必须保留，t-t-link必须割去。工程中，通过将s-t-link权值设置为超级大值，t-t-link设置为0。保证一定仅仅割去t-t-link，否则一定不是最小割，因为当前w(s-t-link)权值是超级大值，割去这条边的代价一定是最大的。

           b.反之同理。

2).非种子点的t-link权值：通过正负类种子点，我们能建立2类的颜色直方图。将直方图归一化成概率密度函数，定义为H_F，H_B。其中s-t-link权值为-ln(H_F(x))，t-t-link权值为-ln(H_B(x))，x为该像素点颜色值。

3).n-link权值：n-link用于度量相邻像素点之间颜色的差异性。设一对相邻点Pi，Pj，则n-link(Pi-Pj)的权值w等于：

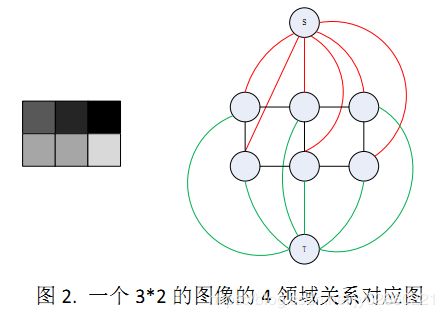
         其中，dist()是距离函数，表示点之间的图像距离。即4领域下，所以领域点距离均为1,；8领域下，对角像素点距离为；在5*5领域下，对角像素点距离为。

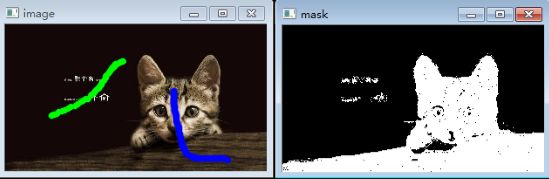
         设种子点的超级大值是1000，=1。图像是3*2的灰度图，数字表示灰度值，红色和蓝色节点表示用户选择的正负种子点。当然种子点过少时，计算的H_F，H_B可能不准，可将种子点附近的像素点也算入先验直方图中，往往可以取得更好效果。

  

       如上图所示，将所有边的权值赋值后，图就建立完毕。剩余则直接运用最小割算法即可求解。最小割算法有很多，包括graph-cut作者提出的快速算法An Experimental Comparison of Min-Cut/Max-Flow Algorithms for Energy Minimization in Vision。Opencv即采用该算法计算最小割。

3.建立图的代码实现：

void GCApplication::graphConstruct(const Mat& img, GCGraphMy& graph)
{
    lambda = 1000;//极大值
    beta = calcBeta(*(this->image));

    Mat leftW, upleftW, upW, uprightW;
    calcNWeights(img, leftW, upleftW, upW, uprightW, beta, gamma);

    int vtxCount = img.cols*img.rows,
        edgeCount = 2 * (4 * img.cols*img.rows - 3 * (img.cols + img.rows) + 2);

    fillSeedToMask(this->mask);
    calSeedPHist(img, this->mask);

    graph.create(vtxCount, edgeCount);
    Point p;
    double a = 1.5;
    for (p.y = 0; p.y < img.rows; p.y++)
    {
        for (p.x = 0; p.x < img.cols; p.x++)
        {
            // add node
            int vtxIdx = graph.addVtx();
            Vec3b color = img.at(p);

            // set t-weights
            double fromSource, toSink;
            if (mask.at(p) == 0)//非种子点的t-link
            {
                fromSource = -a*log(calBgdPrioriCost(color));
                toSink = -a*log(calFgdPrioriCost(color));
            }
            else if (mask.at(p) == MASK_BG_COLOR)//负种子点t-link
            {
                fromSource = 0;
                toSink = lambda;
            }
            else if (mask.at(p) == MASK_FG_COLOR) //正种子点t-link
            {
                fromSource = lambda;
                toSink = 0;
            }
            graph.addTermWeights(vtxIdx, fromSource, toSink);

            // set n-link-weights,每个点只需要与左上4个点进行边连接即可,这样可以不重复的添加所有的N-8-edge
            if (p.x>0)
            {
                double w = leftW.at(p);
                graph.addEdges(vtxIdx, vtxIdx - 1, w, w);
            }
            if (p.x>0 && p.y>0)
            {
                double w = upleftW.at(p);
                graph.addEdges(vtxIdx, vtxIdx - img.cols - 1, w, w);
            }
            if (p.y>0)
            {
                double w = upW.at(p);
                graph.addEdges(vtxIdx, vtxIdx - img.cols, w, w);
            }
            if (p.x0)
            {
                double w = uprightW.at(p);
                graph.addEdges(vtxIdx, vtxIdx - img.cols + 1, w, w);
            }
        }
    }
}

 

2)分割效果：

       从实验结果来看，图中如果有多个类，该方法一般不能取得较好结果。对于2类的图像，该方法效果很好，最后仅需再加上一些空洞填补、小区域过滤等操作就好。

3）完整资源代码：https://download.csdn.net/download/jy02660221/10761799，最后鄙视一下CSDN最低下载分数限制。