无重叠子区间问题——以leetcode56、253、435、452为例

LeetCode 253 会议室Ⅱ

Given an array of meeting time intervals consisting of start and end times [[s1,e1],[s2,e2],…] (si < ei), find the minimum number of conference rooms required.

For example,
Given [[0, 30],[5, 10],[15, 20]],
return 2.

题目链接

题解链接：
双指针法和最小堆法
map法

昨天我在考试中遇到了这道题，原题是：

输入一个n表示要输入的通话记录个数，接下来输入n行，每行为逗号相隔的两个整数，两个数字分别代表呼入时间和挂断时间的时间戳。 举例：10,30，表示[10,30)，代表第10秒呼入，第30秒已经挂断，即第30秒可以接入新的来电； 每一行都是一条通话记录，通话记录已经按呼入时间由小到大排序；

输出一个整数；
代表最少需要多少客服，可以满足所有旅客来电不用等待。

6
0,30
0,50
10,20
15,30
20,50
20,65

这道题很重要。是一道无重叠子区间的题，在这之前可以先做一下LeetCode 56题，二者有一些相似。另外452和435题也是类似的。

对于这道题，双指针法和最小堆法是比较好理解的，map法有些惊艳。根据参考题解，我也写了一些自认为便于理解的注释，希望跟大家交流学习。

/*
给定一个会议时间安排的数组，每个会议时间都会包括开始和结束的时间 [[s1,e1],[s2,e2],…] (si < ei)，为避免会议冲突，同时要考虑充分利用会议室资源，请你计算至少需要多少间会议室，才能满足这些会议安排。

输入: [[0, 30],[5, 10],[15, 20]]
输出: 2

输入: [[7,10],[2,4]]
输出: 1
 */
public class LeetCode253 {
    public static void main(String[] args) {
//        int[][] intervals = {{0, 30}, {5, 10}, {15, 20}};
        int[][] intervals = {
                {0, 30},
                {0, 50},
                {10, 20},
                {10, 15},
                {15, 30},
                {10, 20},
                {20, 50},
                {20, 65}};

        LeetCode253 leetCode253 = new LeetCode253();
        int result1 = leetCode253.minMeetingRooms1(intervals);
        int result2 = leetCode253.minMeetingRooms2(intervals);
        int result3 = leetCode253.minMeetingRooms3(intervals);

        System.out.println(result1);
        System.out.println(result2);
        System.out.println(result3);
    }

    /**
     * 分别对起始时间和结束时间排序，由于会议之间并无差异，所以分别使用两个指针来推进起始时间和结束时间。
     * 题解1：https://blog.csdn.net/jmspan/article/details/51093343
     * 题解2：https://segmentfault.com/a/1190000016524274
     */
    private int minMeetingRooms1(int[][] intervals) {
        if (intervals.length == 0) {
            return 0;
        }

//        int max = 0;
        int rooms = 0;

        int[] startTime = new int[intervals.length];
        int[] endTime = new int[intervals.length];
        for (int i = 0; i<intervals.length; i++){
            startTime[i] = intervals[i][0];
            endTime[i] = intervals[i][1];
        }

        Arrays.sort(startTime);
        Arrays.sort(endTime);

        int i = 0;
        int j = 0;
        while (i < startTime.length && j < endTime.length){
            if (startTime[i] < endTime[j]){
                rooms++;
//                i++;
            }else{
//                rooms--;
                j++;
            }
            i++;
//            max = Math.max(rooms, max);
        }

        return rooms;
    }

    /**
     * 对起始时间进行排序，使用 最小堆 来记录当前会议的结束时间，当新会议的起始时间大于最小堆中的最早结束时间，说明新会议与堆中的最早结束会议不重叠。
     */
    private int minMeetingRooms2(int[][] intervals) {
//        Arrays.sort(intervals, new Comparator() {
        Arrays.sort(intervals, (i1, i2) -> Integer.compare(i1[0], i2[0]));

        PriorityQueue<Integer> minHeap = new PriorityQueue<>();

        int rooms = 0;

        for (int i = 0; i < intervals.length; i++) {
            minHeap.offer(intervals[i][1]);
            if (intervals[i][0] < minHeap.peek()) {
                rooms++;
            } else {
                minHeap.poll();
            }
        }

        return rooms;
    }

    /**
     * 将开始的时间map成+1，结束的时间map成-1；最后遍历，和最大的时候就是min room
     * 题解链接：https://blog.csdn.net/Opium_Z/article/details/88374497
     */
    private int minMeetingRooms3(int[][] intervals) {

        Arrays.sort(intervals, (i1, i2) -> Integer.compare(i2[1], i1[1]));

        int[] map = new int[intervals[0][1]+1];

        for (int[] temp : intervals) {
            map[temp[0]]++;
            map[temp[1]]--;
        }

        int sum = 0, max = 0;
        for (int i = 0; i < map.length; i++) {
            sum += map[i];
            max = Math.max(sum, max);
        }

        return max;
    }
}

剩下的三道题都用到了贪心算法，我大致会用了，代码很简单。
基本的流程是先排序，再以终点为界进行计算。

LeetCode 56 合并区间

题目链接

class Solution {
    public int[][] merge(int[][] intervals) {
        if (intervals == null || intervals.length < 2) {
            return intervals;
        }

        //起点排序
        Arrays.sort(intervals, (arr1, arr2) -> Integer.compare(arr1[0], arr2[0]));

        // create a temp arry
        int[] cur = intervals[0];
        // create the output array with unknow size
        List<int[]> res = new ArrayList();

        // loop through each interval
        for(int[] interval: intervals){
            // check overlap 检查重叠
            if(cur[1] >= interval[0]){
                // set the bigger end 找最大的终点
                cur[1] = Math.max(cur[1], interval[1]);
            } else {
                res.add(cur);
                //更新cur
                cur = interval;
            }
        }

        res.add(cur);
        
        return res.toArray(new int[res.size()][]);
    }
}

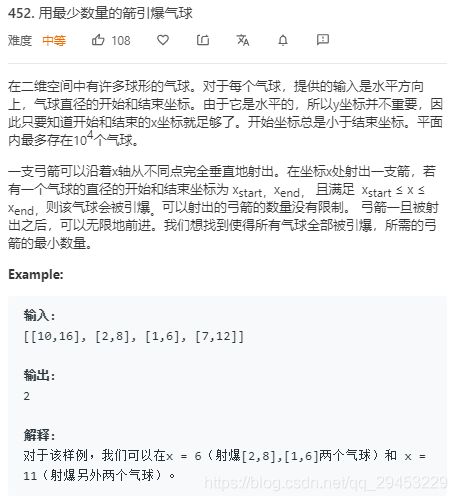
LeetCode 452 用最少数量的箭引爆气球

题目链接

这道题可能是标准的形式了。

从第一个点的终点开始，跟每个点的起点比较，如果起点小于该终点，则说明可以用同一支箭命中；
如果大于等于，则需要另一支箭，此时更新用做比较的点的终点。
最后，返回需要的箭。

class Solution {
    public int findMinArrowShots(int[][] points) {
        int len = points.length;
        if (len < 2) {
            return len;
        }

        //按照末端数字的升序排列
        Arrays.sort(points, (i1, i2) -> Integer.compare(i1[1], i2[1]));

        int limit = points[0][1];
        int count = 1;
        for (int i = 1; i < len; i++) {
            if (points[i][0] > limit) {
                count++;
                limit = points[i][1];
            }
        }

        return count;
    }
}

LeetCode 435

题目链接

452题的目标可以看作是求得了不重复的几个区间（一支箭代表了一个区间）。本题是求变成无重复区间需要拿去的区间数，因此，拿总区间数减这个答案就是本道题的答案了。

需要注意的是，题设区间 [1,2] 和 [2,3] 的边界相互“接触”，但没有相互重叠。因此是intervals[i][0] >= limit。

class Solution {
    public int eraseOverlapIntervals(int[][] intervals) {
        int len = intervals.length;
        if (len < 2) {
            return 0;
        }

        //按照末端数字的升序排列
        Arrays.sort(intervals, (i1, i2) -> Integer.compare(i1[1], i2[1]));

        int limit = intervals[0][1];
        int count = 1;
        for (int i = 1; i < len; i++) {
            if (intervals[i][0] >= limit) {
                count++;
                limit = intervals[i][1];
            }
        }

        return len - count;
    }
}