无参密度估计:KDE和KNN
无参密度估计:KDE和KNN
最大似然估计和贝叶斯估计应用于数据的密度函数形式已知但参数未知的情况,然而并非所有的情况下数据的密度函数的形式是已知的。针对于这种情况,我们可以选择一些无参密度估计方法。
直观上,我们对于概率密度的理解就是单位区域数据出现的概率,公式表示如下:
p ( x ) ≅ k N V p(x) \cong \frac{k}{{NV}} p(x)≅NVk
其中,k是面积是V的区域内数据的个数,N是数据的总个数。对于这个直观,我们可以进行以下证明:
- 假设一个观测变量x来自于一个概率密度为p(x)的分布,那么它落入一个区域R的概率为:
P = ∫ R p ( x ) d x P = \int_R p \left( x \right)dx P=∫Rp(x)dx
假设R非常小,小到R内的p(x)没有变化,那么P就可以根据p(x)和R的面积计算:
P = p ( x ) V ⇒ p ( x ) = P V ( 1 ) P = p\left( x \right)V \Rightarrow p(x) = \frac{P}{V} (1) P=p(x)V⇒p(x)=VP(1)
- 假设现有N个变量来自于概率密度为p(x)的分布,那么其中的k个变量落入区域R的概率可以用一个二项分布描述:
P ( k ) = ( N k ) P k ( 1 − P ) N − k P(k)=\left(\begin{array}{l} {N} \\ {k} \end{array}\right) P^{k}(1-P)^{N-k} P(k)=(Nk)Pk(1−P)N−k
由于二项分布的期望E(k)=NP,可以得到k/N的期望为P:
E ( k N ) = P ⇒ P ≅ k N ( 2 ) E\left( {\frac{k}{N}} \right) = P \Rightarrow P \cong \frac{k}{N}(2) E(Nk)=P⇒P≅Nk(2)
综合(1)(2)可以得:
p ( x ) ≅ k N V ( 3 ) p(x) \cong \frac{k}{{NV}}(3) p(x)≅NVk(3)
核密度估计Kernel Density Estimation (KDE)
我们都很熟悉直方图,在计算密度直方图时首先将样本空间分成若干个采样区域(英文所谓bin),然后通过统计每个区域内落入的样本的个数来近似估计每个区域的中心密度。公式表示为:
P H ( X ) = 1 N 区 域 ( b i n ) 中 样 本 x k 的 个 数 区 域 ( b i n ) 的 采 样 宽 度 {P_H}(X) = \frac{1}{N}\frac{{区域(bin)中样本{x^k}的个数}}{{区域(bin)的采样宽度}} PH(X)=N1区域(bin)的采样宽度区域(bin)中样本xk的个数
计算密度直方图有两个重要控制参数:bin的宽度和第一个bin的开始位置。

密度直方图是一种简单并且直观的模型,但是它不是一个连续的模型。这样的不连续性使得直方图很难表现分布的细节结构,直方图能够展现bin中心位置的概率分布,而在中心之外的位置,特别是bin边缘位置的概率密度就无法展现。为了解决这一问题,我们使用下面的方案计算概率密度:
首先定义一个核函数:
K ( u ) = { 1 ∣ u j ∣ < 1 / 2 ∀ j = 1 , … , D 0 otherwise \mathrm{K}(\mathrm{u})=\left\{\begin{array}{lll} 1 & \left|\mathrm{u}_{\mathrm{j}}\right|<1 / 2 & \forall \mathrm{j}=1, \ldots, \mathrm{D} \\ 0 & \text { otherwise } \end{array}\right. K(u)={10∣uj∣<1/2 otherwise ∀j=1,…,D
即,向量半径在1/2以内记为1,否则为0。
在(3)式中,将计数k利用上面的核函数做如下表示:
KaTeX parse error: Undefined control sequence: \ at position 103: …m{h}}}} \right)\̲ ̲
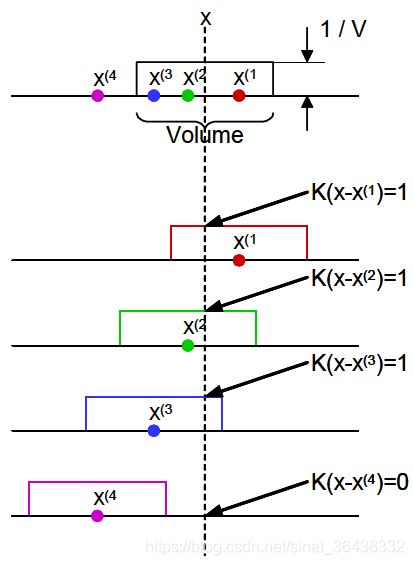
结合核函数的定义,上面的式子可以理解为与x距离在1/2以内的数据点的个数,如下图所示:
假设某一位置x处有三个点x1-x4,其中x1-x3距离x的距离小于1/2,x4距离x的位置大于1/2。此时x点的概率密度为3/V。
进一步的,将V定义为边长为h正多维块的“体积”,概率密度函数可以用下式表示:
p K D E ( x ) = 1 N h D ∑ n = 1 N K ( x − x n h ) {{\rm{p}}_{{\rm{KDE}}}}({\rm{x}}) = \frac{1}{{{\rm{N}}{{\rm{h}}^{\rm{D}}}}}\sum\limits_{{\rm{n}} = 1}^{\rm{N}} {\rm{K}} \left( {\frac{{x - {x^n}}}{{\rm{h}}}} \right) pKDE(x)=NhD1n=1∑NK(hx−xn)
这个公式下,任何一点的概率密度都可以计算出来,这个概率密度就变成一个连续的模型了。
进一步理解核函数
这个核函数,有的文献也叫它Parzen窗,那么为什么又叫它核函数呢?上面概率密度函数的期望:
E [ p K D E ( x ) ] = 1 N h D ∑ n = 1 N E [ K ( x − x D h ) ] = 1 h D E [ K ( x − x D ) h ) ] = 1 h D ∫ K ( x − x ′ h ) p ( x ′ ) d x ′ \begin{array}{l} {\rm{E}}\left[ {{{\rm{p}}_{{\rm{KDE}}}}({\rm{x}})} \right] = \frac{1}{{{\rm{N}}{{\rm{h}}^{\rm{D}}}}}\sum\limits_{{\rm{n}} = 1}^{\rm{N}} {\rm{E}} \left[ {{\rm{K}}\left( {\frac{{x - {x^D}}}{{\rm{h}}}} \right)} \right]\\ = \frac{1}{{{{\rm{h}}^{\rm{D}}}}}{\rm{E}}\left[ {{\rm{K}}\left( {\frac{{\left. {x - {x^D}} \right)}}{{\rm{h}}}} \right)} \right] = \frac{1}{{{{\rm{h}}^D}}}\int {\rm{K}} \left( {\frac{{{\rm{x}} - {{\rm{x}}^\prime }}}{{\rm{h}}}} \right){\rm{p}}\left( {{{\rm{x}}^\prime }} \right){\rm{d}}{{\rm{x}}^\prime } \end{array} E[pKDE(x)]=NhD1n=1∑NE[K(hx−xD)]=hD1E[K(hx−xD))]=hD1∫K(hx−x′)p(x′)dx′
最终可以化为数据点的真实分布p(x’)和核函数K(x)的卷积。为了方便比较,这里列出卷积公式:
∫ − ∞ ∞ f ( τ ) g ( x − τ ) d τ \int_{-\infty}^{\infty} f(\tau) g(x-\tau) d \tau ∫−∞∞f(τ)g(x−τ)dτ
核函数的选取有很多种,除了Parzen窗外,也可以用高斯核:
K ( x ) = 1 ( 2 π ) D / 2 exp ( − 1 2 u ⊤ u ) K(x)=\frac{1}{(2 \pi)^{D / 2}} \exp \left(-\frac{1}{2} u^{\top} u\right) K(x)=(2π)D/21exp(−21u⊤u)
参数h的选择
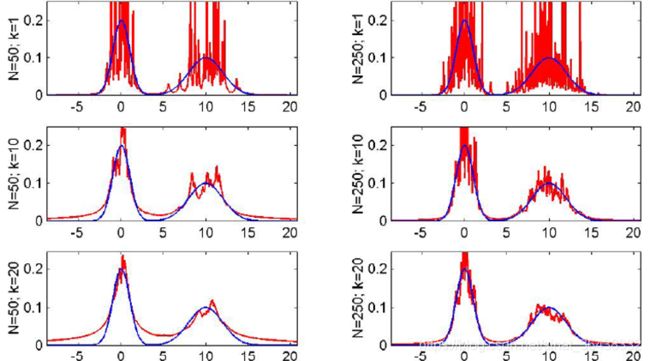
参数h控制着卷积核的大小,h越大,估计出来的密度函数越光滑。
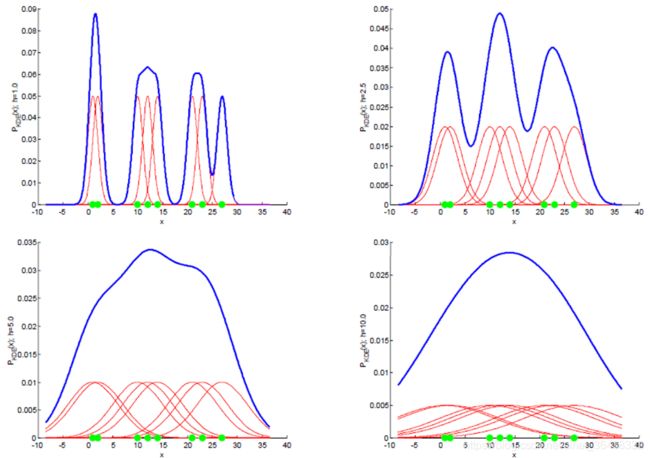 h趋于0时,核函数就成了δ函数,而δ函数与函数f(x)卷积后的结果仍是f(x),所以理论上当h趋于0时,概率密度函数估计值就是其真实值。然而这只是理论上,实际中我们样本的密度是有限的,h太小时,每个点附近的密度估计就不精确,所以h不可能无限小。
h趋于0时,核函数就成了δ函数,而δ函数与函数f(x)卷积后的结果仍是f(x),所以理论上当h趋于0时,概率密度函数估计值就是其真实值。然而这只是理论上,实际中我们样本的密度是有限的,h太小时,每个点附近的密度估计就不精确,所以h不可能无限小。
参数h的选择有下面两种思路:
1.偏差和方差的权衡
如果用均方误差MSE表示密度估计是误差,MSE计算如下:
M S E x ( p K D E ) = E [ ( p K D E ( x ) − p ( x ) ) 2 ] = E [ ( p K D E ( x ) − E ( p K D E ( x ) ) + E ( p K D E ( x ) ) − p ( x ) ) 2 ] = E [ ( p K D E ( x ) − E ( p K D E ( x ) ) ) 2 ] + E [ ( E ( p K D E ( x ) ) − p ( x ) ) 2 ] + E [ 2 ( p K D E ( x ) − E ( p K D E ( x ) ) ) ( E ( p K D E ( x ) ) − p ( x ) ) ] = E [ ( E ( p K D E ( x ) ) − p ( x ) ) 2 ] ⏟ b i a s + E [ ( p K D E ( x ) − E ( p K D E ( x ) ) ) 2 ] ⏟ v a r i a n c e \begin{array}{l} {{\mathop{\rm MSE}\nolimits} _x}\left( {{{\rm{p}}_{{\rm{KDE}}}}} \right) = {\rm{E}}\left[ {{{\left( {{{\rm{p}}_{{\rm{KDE}}}}({\rm{x}}) - {\rm{p}}({\rm{x}})} \right)}^2}} \right]\\ {\rm{ = E}}\left[ {{{\left( {{{\rm{p}}_{{\rm{KDE}}}}({\rm{x}}){\rm{ - E(}}{{\rm{p}}_{{\rm{KDE}}}}({\rm{x}}){\rm{) + E(}}{{\rm{p}}_{{\rm{KDE}}}}({\rm{x}}){\rm{)}} - {\rm{p}}({\rm{x}})} \right)}^2}} \right]\\ = {\rm{E}}\left[ {{{\left( {{{\rm{p}}_{{\rm{KDE}}}}({\rm{x}}){\rm{ - E(}}{{\rm{p}}_{{\rm{KDE}}}}({\rm{x}}){\rm{)}}} \right)}^2}} \right] + {\rm{E}}\left[ {{{\left( {{\rm{E(}}{{\rm{p}}_{{\rm{KDE}}}}({\rm{x}}){\rm{)}} - {\rm{p}}({\rm{x}})} \right)}^2}} \right] + \color{red}{\rm{E}}\left[ {2\left( {{{\rm{p}}_{{\rm{KDE}}}}({\rm{x}}){\rm{ - E(}}{{\rm{p}}_{{\rm{KDE}}}}({\rm{x}}){\rm{)}}} \right)\left( {{\rm{E(}}{{\rm{p}}_{{\rm{KDE}}}}({\rm{x}}){\rm{)}} - {\rm{p}}({\rm{x}})} \right)} \right]\\ = \underbrace {{\rm{E}}\left[ {{{\left( {{\rm{E(}}{{\rm{p}}_{{\rm{KDE}}}}({\rm{x}}){\rm{)}} - {\rm{p}}({\rm{x}})} \right)}^2}} \right]}_{{\rm{bias}}} + \underbrace {{\rm{E}}\left[ {{{\left( {{{\rm{p}}_{{\rm{KDE}}}}({\rm{x}}){\rm{ - E(}}{{\rm{p}}_{{\rm{KDE}}}}({\rm{x}}){\rm{)}}} \right)}^2}} \right]}_{{\rm{variance }}} \end{array} MSEx(pKDE)=E[(pKDE(x)−p(x))2]=E[(pKDE(x)−E(pKDE(x))+E(pKDE(x))−p(x))2]=E[(pKDE(x)−E(pKDE(x)))2]+E[(E(pKDE(x))−p(x))2]+E[2(pKDE(x)−E(pKDE(x)))(E(pKDE(x))−p(x))]=bias E[(E(pKDE(x))−p(x))2]+variance E[(pKDE(x)−E(pKDE(x)))2]
MSE可以分解为偏差和方差。公式红色部分为0,这是因为:
E [ 2 ( p K D E − E ( p K D E ) ) ( E ( p K D E ) − p ) ] = 2 E [ p K D E ⋅ E ( p K D E ) − p K D E ⋅ p − E ( p K D E ) 2 + p ⋅ E ( p K D E ) ] = 2 { E [ p K D E ⋅ E ( p K D E ) ] − E [ p K D E ⋅ p ] − E [ E ( p K D E ) 2 ] + E [ p ⋅ E ( p K D E ) ] } = 2 { E ( p K D E ) 2 − E [ p K D E ⋅ p ] − E ( p K D E ) 2 + E [ p ⋅ E ( p K D E ) ] } = E [ p ⋅ E ( p K D E ) − p ⋅ p K D E ] = 0 \begin{array}{l}{\rm{E}}\left[ {2\left( {{{\rm{p}}_{{\rm{KDE}}}}{\rm{ - E(}}{{\rm{p}}_{{\rm{KDE}}}}{\rm{)}}} \right)\left( {{\rm{E(}}{{\rm{p}}_{{\rm{KDE}}}}{\rm{)}} - {\rm{p}}} \right)} \right]\\ = 2{\rm{E}}\left[ {{{\rm{p}}_{{\rm{KDE}}}} \cdot {\rm{E(}}{{\rm{p}}_{{\rm{KDE}}}}{\rm{)}} - {{\rm{p}}_{{\rm{KDE}}}} \cdot {\rm{p}} - {\rm{E(}}{{\rm{p}}_{{\rm{KDE}}}}{{\rm{)}}^2}{\rm{ + p}} \cdot {\rm{E(}}{{\rm{p}}_{{\rm{KDE}}}}{\rm{)}}} \right]\\ = 2{\rm{\{ E[}}{{\rm{p}}_{{\rm{KDE}}}} \cdot {\rm{E(}}{{\rm{p}}_{{\rm{KDE}}}}{\rm{)] - E[}}{{\rm{p}}_{{\rm{KDE}}}} \cdot {\rm{p] - E[E(}}{{\rm{p}}_{{\rm{KDE}}}}{{\rm{)}}^2}{\rm{] + E[p}} \cdot {\rm{E(}}{{\rm{p}}_{{\rm{KDE}}}}{\rm{)]\} }}\\{\rm{ = }}2{\rm{\{ E(}}{{\rm{p}}_{{\rm{KDE}}}}{{\rm{)}}^2}{\rm{ - E[}}{{\rm{p}}_{{\rm{KDE}}}} \cdot {\rm{p] - E(}}{{\rm{p}}_{{\rm{KDE}}}}{{\rm{)}}^2}{\rm{ + E[p}} \cdot {\rm{E(}}{{\rm{p}}_{{\rm{KDE}}}}{\rm{)]\} }}\\{\rm{ = E[p}} \cdot {\rm{E(}}{{\rm{p}}_{{\rm{KDE}}}}{\rm{) - p}} \cdot {{\rm{p}}_{{\rm{KDE}}}}{\rm{]}}\\{\rm{ = 0}}\end{array} E[2(pKDE−E(pKDE))(E(pKDE)−p)]=2E[pKDE⋅E(pKDE)−pKDE⋅p−E(pKDE)2+p⋅E(pKDE)]=2{E[pKDE⋅E(pKDE)]−E[pKDE⋅p]−E[E(pKDE)2]+E[p⋅E(pKDE)]}=2{E(pKDE)2−E[pKDE⋅p]−E(pKDE)2+E[p⋅E(pKDE)]}=E[p⋅E(pKDE)−p⋅pKDE]=0
其中,偏差代表的是估计的系统误差;而方差代表由于样本采样导致的随机误差。往往减小偏差会增大方差,反之也是如此。当卷积核h比较大时,采样的数据点比较多,因此随机误差(方差)会比较小,但是会导致偏差的增大,反之亦然。较好的h是偏差和方差权衡的结果,如果我们假设样本分布是高斯分布,并利用高斯核估计密度函数,最优的h=1.06σN^(-0.2),其中σ是样本方差,N是训练样本个数。
2.最大似然交叉验证
可以借鉴最大似然的方法利用留一交叉验证寻找最优的h。此时,目标函数为:
h = argmax h { 1 N ∑ n = 1 N log p − n ( x ( n ) ) } where p − n ( x ( n ) ) = 1 ( N − 1 ) h ∑ m = 1 , n = m N K ( x ( n − x ( m ) h ) \begin{aligned}h &=\underset{h}{\operatorname{argmax}}\left\{\frac{1}{N} \sum_{n=1}^{N} \log p_{-n}\left(x^{(n)}\right)\right\} \\& \text { where } p_{-n}\left(x^{(n)}\right)=\frac{1}{(N-1) h} \sum_{m=1, n=m}^{N} K\left(\frac{\left.x^{(n}-x^{(m}\right)}{h}\right)\end{aligned} h=hargmax{N1n=1∑Nlogp−n(x(n))} where p−n(x(n))=(N−1)h1m=1,n=m∑NK(hx(n−x(m))
K临近K Nearest Neighbor (KNN)
KDE和KNN本质上都是遵循公式(3)的算法,不同的是:KDE是固定体积V而去想办法计算k;KNN是固定k而想办法计算V。KNN的公式如下:
P ( x ) ≅ k N V = k N ⋅ c D ⋅ R k D ( x ) P(x) \cong \frac{k}{N V}=\frac{k}{N \cdot c_{D} \cdot R_{k}^{D}(x)} P(x)≅NVk=N⋅cD⋅RkD(x)k
其中,R为估计点x到其第k临近的样本的距离,c是单位范围的体积。这个公式看起来很复杂,这是因为它扩展到D维的情况。其实kNN的思想很简单:计算x点附近恰好包含k个临近样本点的球的体积,k/N/体积就是点x的概率密度。KNN很简单,但是也有很多不足,比如容易受到噪声干扰、分布重尾、有不连续点等。