算法分析-动态规划电路布线问题

一、问题描述
\quad \quad 在一块电路板的上、下两端分别有 $n$ 个接线柱。根据电路设计，要求用导线 $(i,\pi (i))$ 将上端接线柱 $i$ 与下端接线柱 $\pi (i)$ 相连。如下图所示，其中，$\pi (i),1\le i\le n$, 是｛1,2,…,n｝的一个排列。导线 $(I,\pi (i))$ 称为该电路板上的第 $i$ 条连线。对于任何 $1\le i\le j\le n$, 第i条连线和第j条连线相交的充要条件是 $\pi (i)>\pi (j)$.

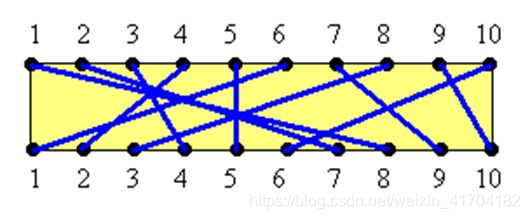
$$\pi （i）=｛8，7，4，2，5，1，9，3，10，6｝$$ \quad \quad 在制作电路板时，要求将这 $n$ 条连线分布到若干绝缘层上。在同一层上的连线不相交。电路布线问题要确定将哪些连线安排在第一层上，使得该层上有尽可能多的连线。换句话说，该问题要求确定导线集 $Nets=｛(i，\pi (i))，1\le i\le n\}$ 的最大不相交子集。
1）同一层电路布线可以如下

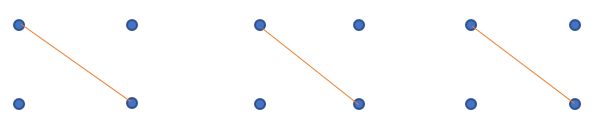
2）同一层电路布线不可能如下

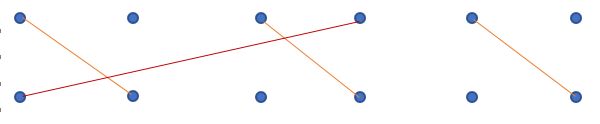
二、最优子结构性质
\quad \quad 记 $N(i,j)=\{t|(t,\pi (t))\in Nets，t\le i,\pi (t)\le j\}$。$N(i,j)$的最大不相交子集为 $MNS(i,j)$。$Size(i,j)=|MNS(i,j)|$。

(1) 当 $i=1$,
$$MNS(1,j)=N(1,j)=\{\begin{array}{l}0,j<\pi (1)\\ 1,j\ge \pi (1)\end{array}$$

(2) 当 $i>1$时，
1）$j<\pi (i)$ 时，$(i,\pi (i))\notin N(i,j)$，在这种情况下，$N(i,j)=N(i-1,j)$, 从而 $Size(i,j)=Size(i-1,j)$。
2）$j\ge \pi (i)$,此时，若 $(i,\pi (i))\in N(i,j)$,则对于任意的 $(t,\pi (t))\in MNS(i,j)$,有 $t<i$ 且 $\pi (t)<\pi (i)$,否则，$(i,\pi (i))$ 与 $(t,\pi (t))$ 相交。在这种情况下 $MNS(i,j)-\{(i,\pi (i))\}$ 是 $N(i-1,\pi (i)-1)$ 的最大不相交子集。

三、递归计数最优值
电路布线的最优值 $Size(n,n)$,由该问题的最优子结构性质可知：
(1) 当 $i=1$,
$$Size(1,j)=\{\begin{array}{l}0,j<\pi (1)\\ 1,j\ge \pi (1)\end{array}$$
(2) 当 $i>1$ 时，
$$Size(i,j)=\{\begin{array}{l}Size(i-1,j),j<\pi (i)\\ max\{Size(i-1,j),Size(i-1,\pi (i))+1\},j\ge \pi (i)\end{array}$$
四、自顶向下计算最优值

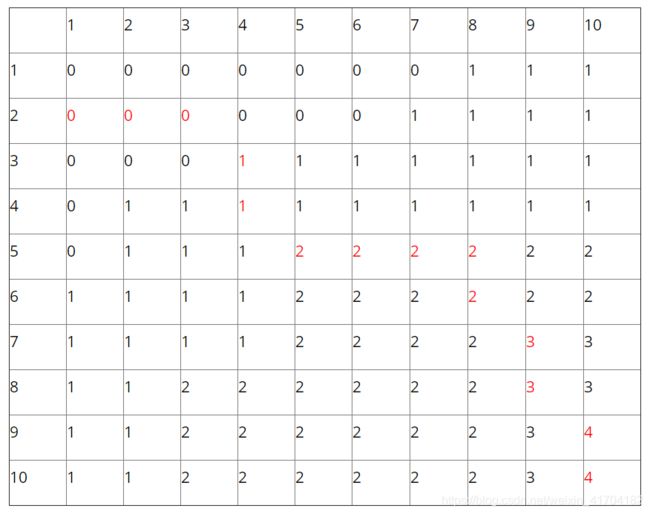
在斜角值改变时可以取得所求的子集。即(9,10),(7,9),(5,5)(3,4)