看完这篇还不会KMP算法,你打我

看完这篇还不会KMP算法你打我

1.引入

​ 这里有一个需求是这样的，我有一个字符串 s1 = “AABAA”,请找到子字符串"AB"在源字符串中的角标。
这里以后都称源字符串为 主串，称子串为模式串。

2.常规思路

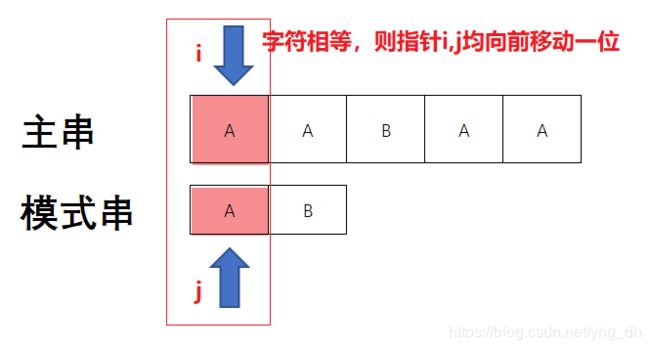
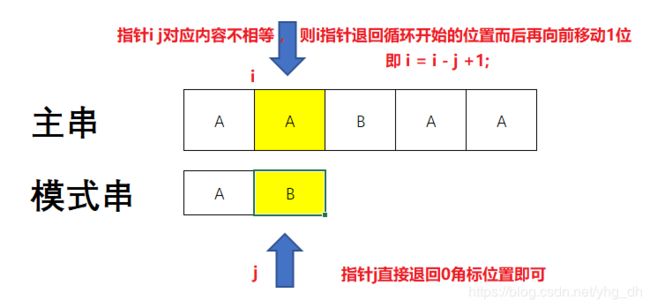
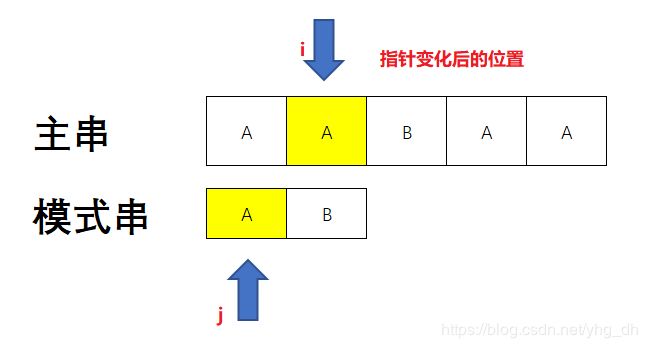
​ 使用两个变量，让这两个变量一开始分别指向字符串的首字符，而后一个一个依次比对，如果字符相等，则两个变量都向前移动一位，指向下一个字符，如果不相等则将主串的指针退回去原来的起始位置，而后再往前移动一位，因为已经判断过前面那位不匹配，所以下次循环开始的时候判断下一个。对于模式串而言，只要将指针移回首字符的位置即可开始下一次匹配。当有一次匹配结束后，模式串的指针移动到模式串外了，那么就找到了匹配的串了，这时候只要将主串的指针往回走就可以计算出起始位置了。
​ 看字如果有耐心的话，应该也懂了，但是怕你们打我还是给你们画画图吧。

之后在匹配两次就能很愉快的找到答案了，相信各位这么聪明，肯定能看懂的，我就不画了。
从上面的画图中可以看出这种算法的思路就是，假设主串的每一个字符都可能是模式串的首字符，而后遍历判断，这是一种相当耿直的算法，可以解决问题，但是会造成重复匹配，程序的执行效率一般，i , j指针会频繁的回溯。

Duang，Duang，Duang这时有三位老哥觉得这个算法太low了，一点都不上流。提出了他们的算法，也就是K.M.P算法，由D.E. Knuth、J.H.Morris和V.R. Pratt三位老大哥的英文名首字母组成，这很算法。

3.K.M.P算法

经过前面举的例子，你们肯定觉得我黄某人真短，才比较两个长度的模式串，这回就给长的。

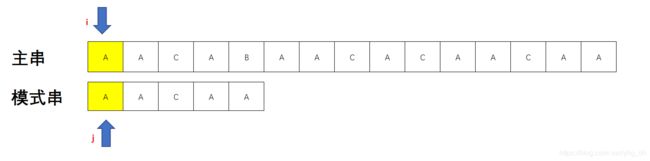
主串：AACAB AACAC AACAA

模式串：AACAA

注意：i j 分别保存的是角标值，同时也可以理解为i j指针的角标值代表了指针前共有多少个元素

话不多少，上图

我们先暂时以常规思路处理到不匹配的位置，经过四次匹配来到如图的位置

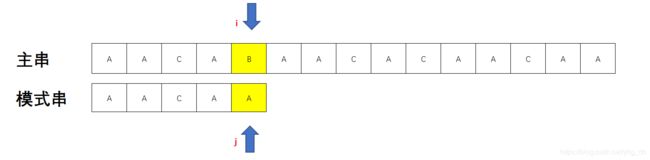
进行第五次匹配的时候可以发现 ij对应字符不匹配 ，那么KMP三位大佬就要开始秀起来了，此时你已经知道了前面的AACA四个字符是你已经匹配过的了，且第五个字符不匹配，所以主串前面3个字符肯定不会是我们想要的模式串的起始位置。
这里我为什么敢这么肯定前三个字符不会是我们想要的模式串的开头字符呢？

因为我手上有一个next数组，next数组告诉我当有四个字符能够匹配上而第五个字符不匹配的时候，我可以从第二个字符重新开始接着匹配。（这里i不需要回溯，只要回溯模式串的指针j到第二个字符A开始重新匹配就可以了）

那么这个next数组又是何方神圣？为什么敢这么肯定，我只要回溯j指针而不用回溯i指针就可以接着匹配？而且为什么是回到那个位置就可以接着匹配？这就涉及到next数组的构成方式了。

next数组的构成理解

kmp三位爷是这么想的，假设我已经匹配了n 个字符，再匹配第n+1个字符的时候没匹配上。那么我之前匹配的n个字符，就当成垃圾丢弃吗，未免太过可惜。有没有什么办法废物利用一下？

指针j为什么可以回溯到k这个位置

这时候他们想到了看看之前匹配的n个字符里面存不存在前k个字符 和倒数k个字符是一样的，同时让k尽可能大，如果存在就可以把之前匹配的n个字符的后k个字符看成是下一次匹配的开头，因为它和模式串的开头(前k和后k)是一模一样的，而且我已经匹配验证过了，所以下一次匹配我只需要从模式字符串的第 k +1 个字符开始继续匹配(这就说明了为什么指针j可以直接回溯到模式串k角标)就可以了。

指针i为什么可以不移动？

还有一个问题就是为什么i指针可以不动，难道k-1位置就不可以作为开头吗，还是从“前k个字符 和倒数k个字符是一样的，同时让k尽可能大”这句话入手，这三位爷这个方法已经从字符串的尾部开始寻找可以作为模式串开头的字符串了，所以倒数k个字符之前不存在可以作为开头的字符，如果可以它就会被纳入k了，所以指针i前面的那些字符，除了最后k个字符都是无用的，这就解释了为什么指针i可以不移动。

为什么需要next数组？

那么是不是每次发现不匹配就去计算一次这个k是多少呢？大可不必，因为模式字符串的长度总是有限的（无线的就不用闹了），那么所有的不匹配的情况也是有限的，要么第一次就不匹配，要么第二次就不匹配，以此类推，一直匹配到字符串的倒数第二个字符不匹配，我们就把所有的不匹配的情况都掌握了，然后我们把这些所有的情况对应的k值都存到next数组里，下次只需要看前面有多少个匹配的字符就知道j指针应该回到模式串哪个位置了。

那么我们怎么从next数组里面取出对应情况的k呢？

假设数组的角标为x,那么x可以理解成 i 指针前共有x个字符已经完成了对模式串的匹配，角标对应位置存放的内容是k，即next[x] == k，有了k我们就知道当发生不匹配的情况我们要把j指针回溯到哪里了。

next[j] == k

next[j] == k

next[j] == k这个公式实在太重要了所以我写了三次，见谅

举例来说就是 如果有next[2] == 1 那么表示第三次匹配的时候不匹配了，前面2个字符完成了匹配，且完成匹配的两个字符中，前一个字符和后一个字符是相等的，第三次匹配失败的时候我们需要将j指针回溯到k角标的位置。这里对于next数组的理解非常重要

再举2个例子帮助大家理解：

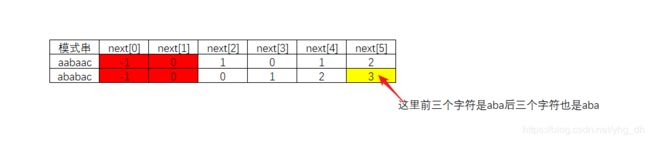
这里我们可以看到next[0] , next[1] 都是固定的，为什么是固定的呢？

为什么next[0] = -1 ; next[1] = 0 ;这两个数值是固定的呢？

首先字符串长度要大于等于2才有讨论这个的价值，就不分析了吧。

在讨论这个之前，我们先回顾一下根据三位爷的思路，

1. 要是i j 所指的内容相同那么就这两个指针均向前移动一位，而后进行下一次比较
2. 要是i j 所指内容不同那么就保持i 指针不动，移动j指针到模式串k角标的位置，进行下一次 i j内容的比较

乍一看之下好像没有什么问题，但是有种特殊情况是，当前i j 指针对应的内容不匹配且 i 指针前没有任何元素已经匹配成功，也就是目前主串还没有找到模式串的首字符，这个时候我们在按照上面的思路去移动j 指针就显得很不合理，因为j指针已经没有可以移动的位置 了，且这里明显应该移动i指针在主串中寻找可以作为模式串首字符的字符，所以对于这种特殊情况我们把 k 值设成 -1 也就是 next[0 ] = k = -1，然后发生了这种特殊情况的时候就把指针j移动到模式串开始前的一个位置，然后进入下一次比较。

这里为每次比较的时候增加一个条件，判断是否 k ==-1 如果是那么就移动j 指针到0角标的位置（也就是j++）， i 指针向前移动一位（也就是i++），这种移动方式是不是很熟悉？没错，这种移动方式和i j内容相同时移动方式是一样的。

所以三位爷的完整思路就是

1. 要是i j 所指的内容相同或者上一次比较的时候连一个都没有匹配成功的时候，那么这两个指针均向前移动一位，而后进行下一次比较
2. 要是i j 所指内容不同那么就保持i 指针不动，通过next数组获取k ,然后移动j指针到模式串k角标的位置，进行下一次 i j内容的比较

最后就是next[1]了，这里只是一个小的逻辑推理，可以不写不看。分析知道i指针前只有一个元素匹配成功，也就谈不上什么首尾相同，首尾相同必须要两个字符以上才可以，所以和上面的情况是类似的，这里表明第二个字符就匹配不上了，那么必然的主串前面那个匹配成功的也就废了，因为i所指的字符和模式串第二个不匹配，接下来就是移动j指针回到角标0的位置，然后匹配i,j是否相同。

说了这么多，大家肯定发现了，三位爷的思路不难理解，全靠next数组去移动 j 指针，那么next数组怎么得到呢

next数组的获得

只要模式串的长度大于2那么，那么next[0] = -1 ; next[1] = 0;都是确定的，下面说明如何获得角标2之后的next数组内容

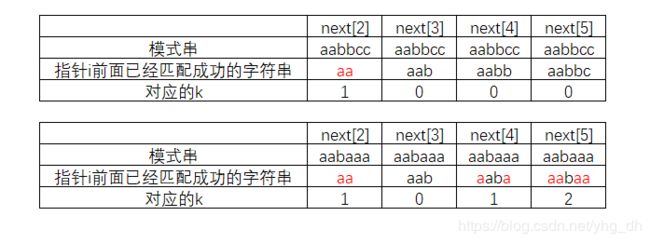
在说明怎么获得前，我们先看看小案例有2个字符串"aabbcc","aabaaa"我们可以很容易的通过肉眼得到next数组

观察红字是不是感觉有规律?但是还是不太清楚？没关系，我们以第二个为例子拆分一下，每个步骤。

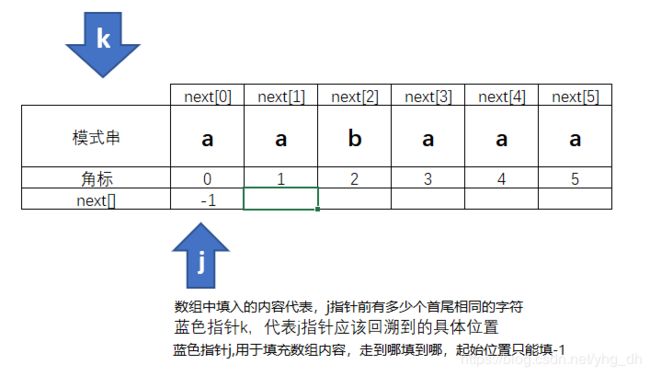
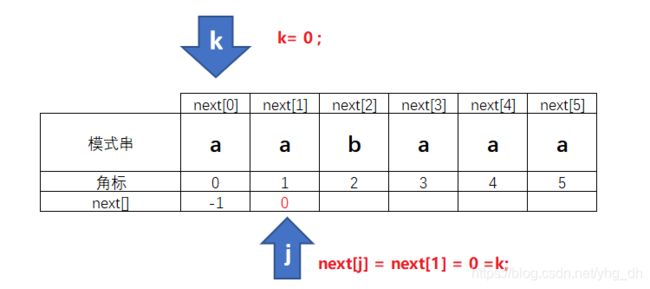
所有next刚生成的时候都是这样的，next [0] = -1 是必然的。

前面我们说过next 数组中 角标具有特殊意义，应该理解成 这样

1. next[j] 这个j角标位置保存的内容是当主串模式串已经成功匹配j个字符而j+1个字符不匹配的时候我的j 指针应该回退到的那个位置
2. 所以next[0] 代表的是一种特殊情况，即i指针前一个都没有匹配成功，那么我们应该在这种不匹配的时候去移动i指针，这里用 -1这个特殊值记录这个情况，所以所有的next数组 next[0] ==-1;
   

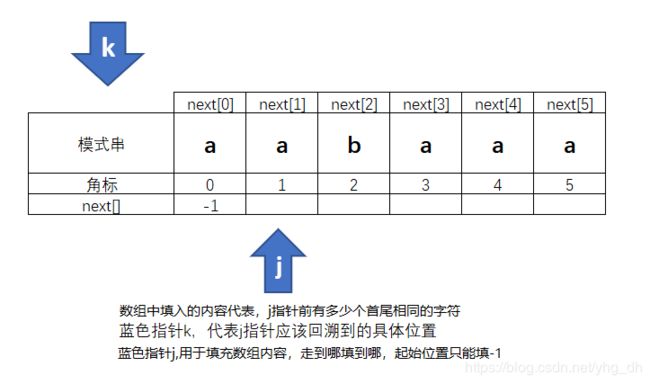
此时next[0] 的值已经确定，所以我们移动j 指针来确定下一个位置next[j]的值

1. 继续分析next[1] 这个位置，它意味着 主串模式串在匹配成功一个字符后发生了不匹配，j指针需要退回的位置，也就是下次需要退回去模式串的第一个字符重新开始匹配
2. 此时只要把j 指针退回 0 角标位置就可以了，这样下次 i j 比较的时候就又可以开始从头比较
3. 所以有next [1] == 0 , 要记住k 的值 就是 next[j]的值，所以j 的任何变动都要同步变动k 指针

此时这个图表明k 指针前有k个元素（不包括k所指元素） 等于 j指针的前k 个元素（不包括j所指元素）

那么我们如果比较 此时 k j 指针所指内容发现 ，有两种情况

1. 要么k j 指针所指内容相同，且已知k 指针前有k个元素（不包括k所指元素） 等于 j指针的前k 个元素（不包括j所指元素），那么我们就知道了 【0~k】==【j-k-1, j】, 简单的说就是两个相同的字符串再分别在末尾加一个相同的字符，得到的两个新的字符串肯定也是一样的。

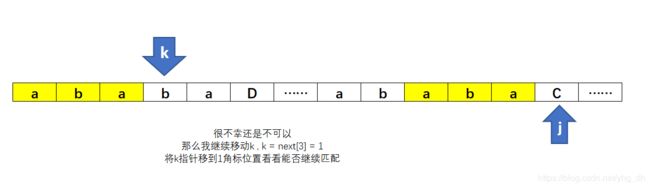
2. 要么k j指针所指内容不同，这个情况相当之复杂，仔细分析一下手上有的内容

   ​ 现在已经知道k j 指针前的k个字符是一样的，那么在这k个字符中存不存在一个k1使得这k个字符的前k1个字符等于后k1个字符？答案是肯定存在的毕竟 next[k]我们是知道的而且也已经求过这个数据了。所以下次比较的时候我们就看看用k1个字符作为开头能不能让 k1 j 指针所指内容相同，如果相同就愉快的回到第一种情况，如果还不相同，就继续执行第二种情况的处理方式，k2 = next[k1],以此类推。那么当kn == -1的时候说明没有任何元素可以继续作为模式字符串进行匹配，那么我们就直接按照 k = -1的情况去处理就好了。

   这里烧脑了，举个例子吧。假设我现在已经知道ababa ……ababa是前后有五个相同的字符ababa。
   
   
   

通过这几个图片，可以找到规律，就是

1. 如果j指针后面的那一个元素 和 k指针后面那一个元素相等，那么就可以k j 指针一起向前移动一位，同时在j第一次来到这个位置的时候将k 的新位置保存在next[j] 中
2. 如果j指针后面的那一个元素 和 k指针后面那一个元素不相等，那么先将k指针移动到next[k]的位置，然后进入下一次循环继续判断，看看用稍短一点的字符串作为模式串的开头能否匹配成功
3. 如果k ==-1了说明这个j指针所在的位置不可能作为模式串的一部分所以直接放弃这个位置，将两个指针同时前移就好了

K.M.P算法实现

好了，感谢各位看官的支持，到这一步了我觉得以大家的聪明才智肯定已经完全理解了三位爷的思路，我们现在只需要写写代码就好了。

public class FindSubStrTest {
    //
    public static void main(String[] args) {
        int index = findSubStr("ababc", "abc");
        System.out.println(index);//输出2

    }
    public static int findSubStr(String src , String sub){
        //创建两个指针指向两个字符串的头部
        int i = 0 , j = 0;
        //获取next数组
        int[] next = getNext(sub);
        while(i<src.length()&&j<sub.length()){
            if(j == -1 || src.charAt(i) == sub.charAt(j)){
                i++;
                j++;
            }else{
                j = next[j];

            }

        }
        if( j == sub.length() ){
            return i-sub.length();
        }
        return -1;
    }
    public static int[] getNext(String sub){
        int[] next = new int [sub.length()];
        next[0] = -1 ;
        //next[1] = 0 ;这个可写可不写
        int k = -1;
        for(int j = 0; j< next.length-1;){
            if(k == -1 || sub.charAt(j) == sub.charAt(k)){
                k++;//这两行代码可以和下面的最后一行合并秀一下
                j++;//这两行代码可以和下面的最后一行合并秀一下，个人不是很喜欢
                next[j] = k;
            }else{
                k = next[k];
            }
        }
        return next;
    }
}

//喜欢的觉得有点帮助的点个赞，留个言吧。

//如果还有不懂的你来打我，我躺平了，来吧。