深度学习与PyTorch笔记12
随机梯度下降
什么是梯度
导数(derivate):反映y随x变化的趋势。标量 d d d
偏微分(partial derivate):一个函数对其自变量的变化的描述程度。标量 ∂ \partial ∂。导数的特殊情况。
z = y 2 − x 2 z=y^{2}-x^{2} z=y2−x2
∂ z ∂ x = − 2 x ∂ z ∂ y = 2 y \frac{\partial z}{\partial x }=-2x\qquad\frac{\partial z}{\partial y }=2y ∂x∂z=−2x∂y∂z=2y
梯度(gradient):所有的偏微分组成的一个向量。 ∇ f = ( ∂ f ∂ x 1 ; ∂ f ∂ x 2 ; . . . ; ∂ f ∂ x n ) \nabla f=(\frac{\partial f}{\partial x_{1}};\frac{\partial f}{\partial x_{2}};...;\frac{\partial f}{\partial x_{n}}) ∇f=(∂x1∂f;∂x2∂f;...;∂xn∂f)
1、梯度的长度从某种反面反映了函数变化的趋势,增长的速率。
2、梯度的方向代表函数增长的方向。
How to search for minima?
θ t + 1 = θ t − α t ∇ f ( θ t ) \theta_{t+1}=\theta_{t}-\alpha_{t}\nabla f(\theta_{t}) θt+1=θt−αt∇f(θt)
θ t \theta_{t} θt函数当前值, ∇ f ( θ t ) \nabla f(\theta_{t}) ∇f(θt)当前值梯度, α t \alpha_{t} αt一个比较小的learning rate。
举个栗子:
function:
J ( θ 1 , θ 2 ) = θ 1 2 + θ 2 2 J(\theta_{1},\theta_{2})=\theta^{2}_{1}+\theta^{2}_{2} J(θ1,θ2)=θ12+θ22
objective:
min θ 1 , θ 2 J ( θ 1 , θ 2 ) \min_{\theta_{1},\theta_{2}}J(\theta_{1},\theta_{2}) θ1,θ2minJ(θ1,θ2)
update rules:
θ 1 ′ = θ 1 − α d d θ 1 J ( θ 1 , θ 2 ) \theta^{'}_{1}=\theta_{1}-\alpha\frac{d}{d\theta_{1}}J(\theta_{1},\theta_{2}) θ1′=θ1−αdθ1dJ(θ1,θ2)
θ 2 ′ = θ 2 − α d d θ 2 J ( θ 1 , θ 2 ) \theta^{'}_{2}=\theta_{2}-\alpha\frac{d}{d\theta_{2}}J(\theta_{1},\theta_{2}) θ2′=θ2−αdθ2dJ(θ1,θ2)
derivatives:
d d θ 1 J ( θ 1 , θ 2 ) = d d θ 1 θ 1 2 + d d θ 1 θ 2 2 = 2 θ 1 \frac{d}{d\theta_{1}}J(\theta_{1},\theta_{2})=\frac{d}{d\theta_{1}}\theta^{2}_{1}+\frac{d}{d\theta_{1}}\theta^{2}_{2}=2\theta_{1} dθ1dJ(θ1,θ2)=dθ1dθ12+dθ1dθ22=2θ1
d d θ 2 J ( θ 1 , θ 2 ) = d d θ 2 θ 1 2 + d d θ 2 θ 2 2 = 2 θ 2 \frac{d}{d\theta_{2}}J(\theta_{1},\theta_{2})=\frac{d}{d\theta_{2}}\theta^{2}_{1}+\frac{d}{d\theta_{2}}\theta^{2}_{2}=2\theta_{2} dθ2dJ(θ1,θ2)=dθ2dθ12+dθ2dθ22=2θ2
初始化 θ \theta θ值, α \alpha α可以取0.001代入公式求解。
影响搜索过程:
1、local minima:局部极小值
2、saddle point:鞍点
3、initialization status:初始状态,一定要初始化,学习何凯明的方法
4、learning rate:学习率,影响收敛速度和精度,一定要小
5、momentum :动量,怎么逃离局部极小值,添加一个动量,可以理解为惯性,下降时惯性大可以把参数从局部极小值推出去。
6、etc.
常见函数梯度
一维函数
| common functions | function | derivative |
|---|---|---|
| constant | c c c | 0 0 0 |
| line | x x x | 1 1 1 |
| a x ax ax | a a a | |
| square | x 2 x^{2} x2 | 2 x 2x 2x |
| square root | x \sqrt{x} x | ( 1 / 2 ) x − 1 / 2 (1/2)x^{-1/2} (1/2)x−1/2 |
| exponential | e x e^{x} ex | e x e^{x} ex |
| a x a^{x} ax | ( l n a ) a x (lna)a^{x} (lna)ax | |
| logarithms | l n ( x ) ln(x) ln(x) | 1 / x 1/x 1/x |
| l o g a x log_{a}x logax | 1 / ( x l n ( a ) ) 1/(xln(a)) 1/(xln(a)) | |
| trigonometry | s i n ( x ) sin(x) sin(x) | c o s ( x ) cos(x) cos(x) |
| c o s ( x ) cos(x) cos(x) | − s i n ( x ) -sin(x) −sin(x) | |
| t a n ( x ) tan(x) tan(x) | s e c 2 ( x ) sec^{2}(x) sec2(x) |
激活函数与Loss的梯度
激活函数及其梯度
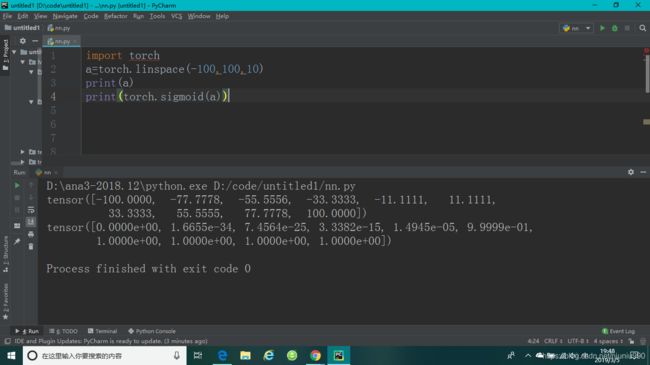
sigmoid/logistic
f ( x ) = σ ( x ) = 1 1 + e − x f(x)=\sigma(x)=\frac{1}{1+e^{-x}} f(x)=σ(x)=1+e−x1
连续,光滑,压缩到(0,1),概率 P r o b ∈ [ 0 , 1 ] Prob\in[0,1] Prob∈[0,1],像素值 R G B ∈ [ 0 , 1 ] RGB\in[0,1] RGB∈[0,1]。
致命缺陷:在正无穷或负无穷处, σ \sigma σ的导数趋近于0,参数长时间得不到更新,出现梯度离散现象。
求导:
d d x σ ( x ) = d d x ( 1 1 + e − x ) = e − x ( 1 + e − x ) 2 = ( 1 + e − x ) − 1 ( 1 + e − x ) 2 = 1 + e − x ( 1 + e − x ) 2 − ( 1 1 + e − x ) 2 = σ ( x ) − σ ( x ) 2 \frac{d}{dx}\sigma(x)=\frac{d}{dx}(\frac{1}{1+e^{-x}})=\frac{e^{-x}}{(1+e^{-x})^{2}}=\frac{(1+e^{-x})-1}{(1+e^{-x})^{2}}=\frac{1+e^{-x}}{(1+e^{-x})^{2}}-(\frac{1}{1+e^{-x}})^{2}=\sigma(x)-\sigma(x)^{2} dxdσ(x)=dxd(1+e−x1)=(1+e−x)2e−x=(1+e−x)2(1+e−x)−1=(1+e−x)21+e−x−(1+e−x1)2=σ(x)−σ(x)2
σ ′ = σ ( 1 − σ ) \sigma^{'}=\sigma(1-\sigma) σ′=σ(1−σ)
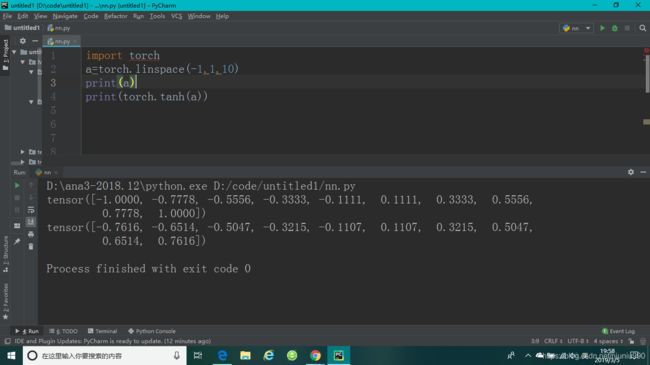
tanh
f ( x ) = t a n h ( x ) = e x − e − x e x + e − x = 2 s i g m o i d ( 2 x ) − 1 f(x)=tanh(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}=2sigmoid(2x)-1 f(x)=tanh(x)=ex+e−xex−e−x=2sigmoid(2x)−1
在RNN中用的比较多。范围[-1,1]。
d d x t a n h ( x ) = ( e x + e − x ) ( e x + e − x ) − ( e x − e − x ) ( e x − e − x ) ( e x + e − x ) 2 = 1 − ( e x − e − x ) 2 ( e x + e − x ) 2 = 1 − t a n h 2 ( x ) \frac{d}{dx}tanh(x)=\frac{(e^{x}+e^{-x})(e^{x}+e^{-x})-(e^{x}-e^{-x})(e^{x}-e^{-x})}{(e^{x}+e^{-x})^{2}}=1-\frac{(e^{x}-e^{-x})^{2}}{(e^{x}+e^{-x})^{2}}=1-tanh^{2}(x) dxdtanh(x)=(ex+e−x)2(ex+e−x)(ex+e−x)−(ex−e−x)(ex−e−x)=1−(ex+e−x)2(ex−e−x)2=1−tanh2(x)
rectified linear unit(ReLU)
目前使用最多,简单有效。
f ′ ( x ) = { 0 for x < 0 x for x ≥ 0 f^{'}(x)= \begin{cases} \mathcal{0} &\text{for $x<0$}\\ \mathcal{x} &\text{for $x\ge0$} \end{cases} f′(x)={0xfor x<0for x≥0
梯度不变,不容易出现梯度离散和梯度爆炸。
LOSS及其梯度
两种常见LOSS。
mean squared error(MSE)
均方差。
l o s s = ∑ [ y − ( x w + b ) ] 2 loss=\sum[y-(xw+b)]^{2} loss=∑[y−(xw+b)]2
L 2 n o r m = ∣ ∣ y − ( x w + b ) ∣ ∣ 2 L2norm=||y-(xw+b)||_{2} L2norm=∣∣y−(xw+b)∣∣2(各元素相减的差的平方和再开根号)
l o s s = n o r m ( y − ( x w + b ) ) 2 loss=norm(y-(xw+b))^{2} loss=norm(y−(xw+b))2
求导:
l o s s = ∑ [ y − f θ ( x ) ] 2 loss=\sum[y-f_{\theta}(x)]^{2} loss=∑[y−fθ(x)]2
∇ l o s s ∇ θ = 2 ∑ [ y − f θ ( x ) ] ∗ ∇ f θ ( x ) ∇ θ \frac{\nabla loss}{\nabla \theta}=2\sum[y-f_{\theta}(x)]*\frac{\nabla f_{\theta}(x)}{\nabla \theta} ∇θ∇loss=2∑[y−fθ(x)]∗∇θ∇fθ(x)
使用pytorch自动求导:
1、torch.autograd.grad(loss.[w1,w2,…])
p r e d = x ∗ w + b pred=x*w+b pred=x∗w+b,使用F.mse_loss(pred,label)函数,得到 ( y − p r e d ) 2 (y-pred)^{2} (y−pred)2,再使用torch.autograd.grad(pred,[w])函数进行求导,但是直接求导会出错,说w参数是不需要求导的,那是因为w初始化的时候没有设置为是需要导数信息的,此时需要对w参数进行更新,使用w.requires_grad_()#_此符号会对w进行更新,告诉pytorch这个w变量是需要grad信息的函数来更新,由于pytorch是做一步计算一步图的,所以还需要对图进行更新。w除了用此方法设置梯度信息外还可以用w=torch.tensor([Initial value],requiregrad=True)来设置。

2、loss.backward()
loss.backward()backword表示向后传播,在完成前面的建图后,pytorch会记录下来图的所有路径,在loss最后的节点调用backward时会自动的往后,从后往前传播,完成这条路径上所有的需要梯度的tensor的梯度的计算方法,计算出来的梯度不会再返回出来,它会自动的把所有的梯度信息附加在每一个tensor的成员变量.grad上。
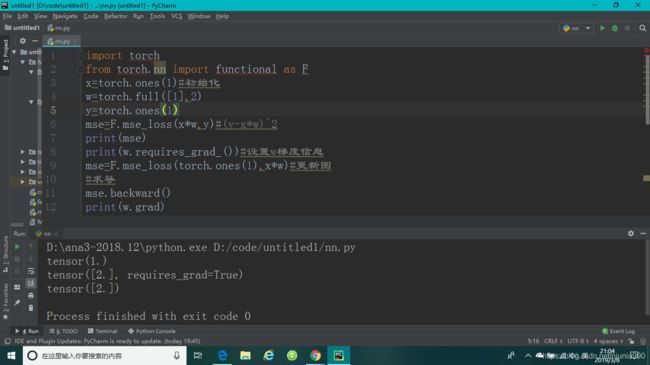
w.norm返回的是tensor本身的一个L2norm,w.grad.norm()返回的是w梯度的norm。
cross entropy loss
用于分类,既可以用于二分类,也可以用于多分类,一般与softmax搭配使用。这里只介绍一下softmax函数。
softmax函数每一个值的区间满足[0,1],所有值加起来的和等于1,非常适合多分类的情况。
S ( y i ) = e y i ∑ j e y j S(y_{i})=\frac{e^{y_{i}}}{\sum_{j}e^{y_{j}}} S(yi)=∑jeyjeyi
把大距离变得更大,小距离变得更小。
p i = e a i ∑ k = 1 N e a k p_{i}=\frac{e^{a_{i}}}{\sum^{N}_{k=1}e^{a_{k}}} pi=∑k=1Neakeai
when i = j i=j i=j,
∂ p i ∂ a j = ∂ e a i ∑ k = 1 N e a k ∂ a j \frac{\partial p_{i}}{\partial a_{j} }=\frac{\partial\frac{e^{a_{i}}}{\sum^{N}_{k=1}e^{a_{k}}}}{\partial a_{j} } ∂aj∂pi=∂aj∂∑k=1Neakeai
f ( x ) = g ( x ) h ( x ) f(x)=\frac{g(x)}{h(x)} f(x)=h(x)g(x)
f ′ ( x ) = g ′ ( x ) h ( x ) − h ′ ( x ) g ( x ) h ( x ) 2 f^{'}(x)=\frac{g^{'}(x)h(x)-h^{'}(x)g(x)}{h(x)^{2}} f′(x)=h(x)2g′(x)h(x)−h′(x)g(x)
g ( x ) = e a i g(x)=e^{a_{i}} g(x)=eai
h ( x ) = ∑ k = 1 N e a k h(x)=\sum^{N}_{k=1}e^{a_{k}} h(x)=k=1∑Neak
∂ e a i ∑ k = 1 N e a k ∂ a j = e a i ∑ k = 1 N e a k − e a j e a i ( ∑ k = 1 N e a k ) 2 = e a i ( ∑ k = 1 N e a k − e a j ) ( ∑ k = 1 N e a k ) 2 = e a i ∑ k = 1 N e a k × ( ∑ k = 1 N e a k − e a j ) ∑ k = 1 N e a k = p i ( 1 − p j ) \frac{\partial\frac{e^{a_{i}}}{\sum^{N}_{k=1}e^{a_{k}}}}{\partial a_{j} }=\frac{e^{a_{i}}\sum^{N}_{k=1}e^{a_{k}}-e^{a_{j}}e^{a_{i}}}{(\sum^{N}_{k=1}e^{a_{k}})^{2}}=\frac{e^{a_{i}}(\sum^{N}_{k=1}e^{a_{k}}-e^{a_{j}})}{(\sum^{N}_{k=1}e^{a_{k}})^{2}}=\frac{e^{a_{i}}}{\sum^{N}_{k=1}e^{a_{k}}}\times\frac{(\sum^{N}_{k=1}e^{a_{k}}-e^{a_{j}})}{\sum^{N}_{k=1}e^{a_{k}}}=p_{i}(1-p_{j}) ∂aj∂∑k=1Neakeai=(∑k=1Neak)2eai∑k=1Neak−eajeai=(∑k=1Neak)2eai(∑k=1Neak−eaj)=∑k=1Neakeai×∑k=1Neak(∑k=1Neak−eaj)=pi(1−pj)
∵ i = j ∴ ∂ p i ∂ a j = p j ( 1 − p j ) \because i=j \therefore\frac{\partial p_{i}}{\partial a_{j} }=p_{j}(1-p_{j}) ∵i=j∴∂aj∂pi=pj(1−pj)
当 i i i不等于 j j j,
∂ e a i ∑ k = 1 N e a k ∂ a j = 0 − e a j e a i ( ∑ k = 1 N e a k ) 2 = − e a j ∑ k = 1 N e a k × e a i ∑ k = 1 N e a k = − p j p i \frac{\partial\frac{e^{a_{i}}}{\sum^{N}_{k=1}e^{a_{k}}}}{\partial a_{j} }=\frac{0-e^{a_{j}}e^{a_{i}}}{(\sum^{N}_{k=1}e^{a_{k}})^{2}}=\frac{-e^{a_{j}}}{\sum^{N}_{k=1}e^{a_{k}}}\times\frac{e^{a_{i}}}{\sum^{N}_{k=1}e^{a_{k}}}=-p_{j}p_{i} ∂aj∂∑k=1Neakeai=(∑k=1Neak)20−eajeai=∑k=1Neak−eaj×∑k=1Neakeai=−pjpi
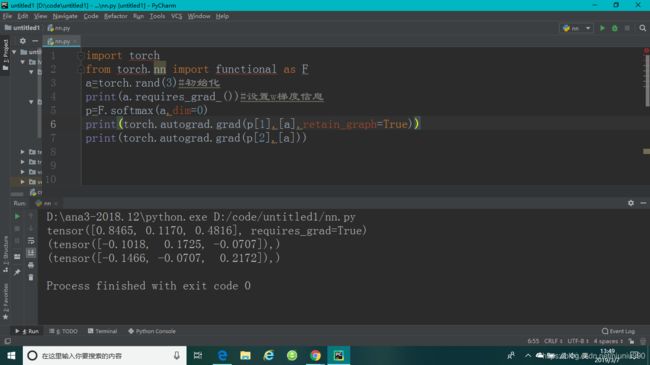
F.softmax(tensor,dim=d)一定要指定维度。
retain_graph=True标志只能保留一次,图就会被清掉。grad和backward后面的loss一定是dim为1长度为1的。