Pytorch：nn.BatchNorm2d()函数
机器学习中，进行模型训练之前，需对数据做归一化处理，使其分布一致。在深度神经网络训练过程中，通常一次训练是一个batch，而非全体数据。每个batch具有不同的分布产生了internal covarivate shift问题——在训练过程中，数据分布会发生变化，对下一层网络的学习带来困难。Batch Normalization将数据拉回到均值为0，方差为1的正态分布上(归一化)，一方面使得数据分布一致，另一方面避免梯度消失、梯度爆炸。
Batch Noramlization 是想让输入满足同一个分布， 那么是让输入的什么特征满足同一分布呢？就是让每张图片的相同通道的所有像素值的均值和方差相同。比如我们有两张图片（都为3通道），我们现在只说R通道，我们希望第一张图片的R通道的均值 和 第二张图片R通道的均值相同，方差同理。
那么在实际运行过程中均值是如何计算的呢？可以有两种方法：
把所有图片的相同通道的值相加，然后求平均数，
也可以先求出每一个图片此通道的均值，然后再求所有图片此通道均值的均值。
1 Internal Covariate Shift
Internal Covariate Shift ：此术语是google小组在论文Batch Normalizatoin 中提出来的，其主要描述的是：训练深度网络的时候经常发生训练困难的问题，因为，每一次参数迭代更新后，上一层网络的输出数据经过这一层网络计算后，数据的分布会发生变化，为下一层网络的学习带来困难（神经网络本来就是要学习数据的分布，要是分布一直在变，学习就很难了），此现象称之为Internal Covariate Shift。
Batch Normalizatoin之前的解决方案就是使用较小的学习率，和小心的初始化参数，对数据做白化处理，但是显然治标不治本。
Internal Shift 和 Covariate Shift具有相似性，但并不是一个东西，前者发生在神经网络的内部，所以是Internal InternalInternal，后者发生在输入数据上。Covariate CovariateCovariate Shift ShiftShift主要描述的是由于训练数据和测试数据存在分布的差异性，给网络的泛化性和训练速度带来了影响，我们经常使用的方法是做归一化或者白化。想要直观感受的话，看下图：
举个简单线性分类栗子，假设我们的数据分布如a所示，参数初始化一般是0均值，和较小的方差，此时拟合的y=wx+b，如b图中的橘色线，经过多次迭代后，达到紫色线，此时具有很好的分类效果，但是如果我们将其归一化到0点附近，显然会加快训练速度，如此我们更进一步的通过变换拉大数据之间的相对差异性，那么就更容易区分了。
2 nn.BatchNorm2d()函数
class torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True)| parameters： | num_features： 一般输入参数为batch_size*num_features*height*width，即为其中特征的数量，channel数。 eps： 为保证数值稳定性（分母不能趋近或取0）,给分母加上的值。默认为1e-5。 momentum： 动态均值和动态方差所使用的动量，即一个用于运行过程中均值和方差的一个估计参数，默认值为0.1。期望和方差的更新公式： affine： 一个布尔值，当设为true，给该层添加可学习的仿射变换参数，即给定可以学习的系数矩阵 |
| shape： | 输入：（N, C，H, W) 输出：（N, C, H, W）（输入输出相同） |
，其中
是估计值，
是新的观测值3 数学原理
-
BatchNorm2d()函数数学原理如下：
其中x为需要归一化的输入数据，
和
为批量数据的均值和方差，
为防止分母出现零所增加的变量，
(gamma)和
(beta)是对输入值进行仿射操作，即线性变换。 和 的默认值分别为1和0，仿射包含了不进行仿射的结果，使得BatchNormlization的引入至少不降低模型， 和 为模型的学习参数。
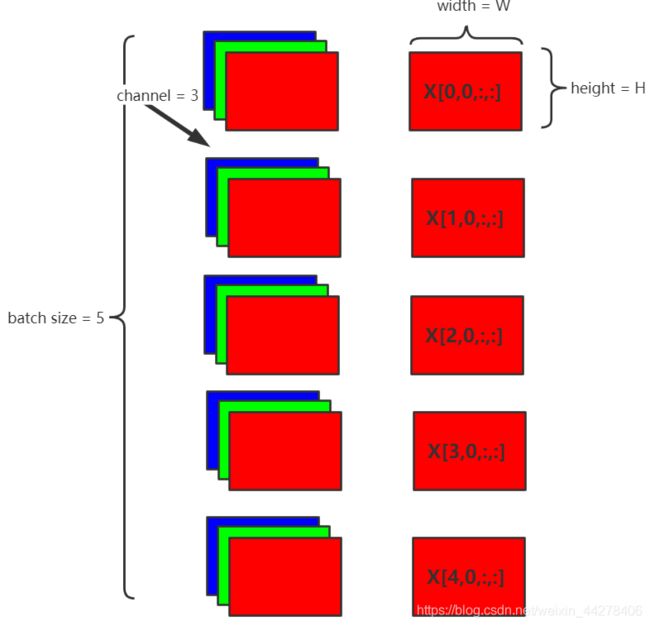
4 图解
假设在网络中间经过某些卷积操作之后的输出的feature maps的尺寸为N×C×W×H，5为batch size（N），3为channel（C），W×H为feature map的宽、高，则Batch Normalization的计算过程如下：
步骤：
- 1.每个batch计算同一通道的均值μ \muμ，如图取channel 0，即c=0 c=0c=0（红色表示）：
![\mu =\frac{\sum_{n=0}^{N-1}\sum_{w=0}^{W-1}\sum_{h=0}^{H-1}X[n, c, w, h]}{N \times W \times H}](http://img.e-com-net.com/image/info8/77ebb105f1054734a21eec0fdda5de50.gif){kind=small}
- 2.每个batch计算同一通道的方差
：
![\sigma ^{2}=\frac{\sum_{n=0}^{N-1}\sum_{w=0}^{W-1}\sum_{h=0}^{H-1}(X[n, c, w, h]-\mu)^{2} }{N \times W \times H}](http://img.e-com-net.com/image/info8/b3d4313248df477db932bc1af5fa668c.gif){kind=small}
- 3.对当前channel下feature map中每个点
，索引形式![X[n, c, w, h]](http://img.e-com-net.com/image/info8/c14c5b24fec04bd4a214eea8f9bc6a67.gif)
，做归一化：
- 4.增加缩放和平移变量
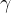和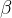 
可学习的仿射变换参数），归一化后的值：
简化公式：
5 代码演示
更具体的演示可看：https://blog.csdn.net/algorithmPro/article/details/103982466
import torch
import torch.nn as nn
#num_features - num_features from an expected input of size:batch_size*num_features*height*width
#eps:default:1e-5 (公式中为数值稳定性加到分母上的值)
#momentum:动量参数，用于running_mean and running_var计算的值，default：0.1
input=torch.randn(1, 2, 3, 4) # 生成一个三维矩阵，bitch_size=1, C=2, H=3, W=4
m=nn.BatchNorm2d(2, affine=True) # 2为输入的通道数，affine参数设为True表示weight和bias将被使用，即 gamma 和 Beta
output=m(input) # 批正则化变换
print(input)
print(m.weight) # gamma
print(m.bias) # Beta
print(output)
print(output.size())
# result
tensor([[[[ 1.4174, -1.9512, -0.4910, -0.5675],
[ 1.2095, 1.0312, 0.8652, -0.1177],
[-0.5964, 0.5000, -1.4704, 2.3610]],
[[-0.8312, -0.8122, -0.3876, 0.1245],
[ 0.5627, -0.1876, -1.6413, -1.8722],
[-0.0636, 0.7284, 2.1816, 0.4933]]]])
Parameter containing:
tensor([1., 1.], requires_grad=True) # gamma
Parameter containing:
tensor([0., 0.], requires_grad=True) # Beta
tensor([[[[ 0.2892, -0.4996, -0.1577, -0.1756],
[ 0.2405, 0.1987, 0.1599, -0.0703],
[-0.1824, 0.0743, -0.3871, 0.5101]],
[[-0.0975, -0.0948, -0.0347, 0.0377],
[ 0.0997, -0.0064, -0.2121, -0.2448],
[ 0.0111, 0.1232, 0.3287, 0.0899]]]],
grad_fn=)
torch.Size([1, 2, 3, 4])
输入是一个1*2*3*4 四维矩阵，gamma和beta为一维数组，是针对input[0][0]，input[0][1]两个3*4的二维矩阵分别进行处理的，我们不妨将input[0][0]的按照上面介绍的基本公式来运算，看是否能对的上output[0][0]中的数据。首先我们将input[0][0]中的数据输出，并计算其中的均值和方差。
# 输入如下结果
输入的第一个维度:
tensor([[ 1.4174, -1.9512, -0.4910, -0.5675],
[ 1.2095, 1.0312, 0.8652, -0.1177],
[-0.5964, 0.5000, -1.4704, 2.3610]])
BatchNorm2d(2, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
m.eps= 1e-05
tensor(0.1825)
tensor(1.4675)
# 通过计算器计算出均值和方差均正确计算。最后通过公式计算input[0][0][0][0]的值，代码如下：
batchnormone=((input[0][0][0][0]-firstDimenMean)/(torch.pow(firstDimenVar,0.5)+m.eps))\
*m.weight[0]+m.bias[0]
print(batchnormone)
# result
tensor(0.2892, grad_fn=)
注：贝塞尔校正系数：
从公式上理解即在计算方差时一般的计算方式如下：
通过贝塞尔校正的样本方差如下：
目的是在总体中选取样本时能够防止边缘数据不被选到
参考：
- https://blog.csdn.net/qq_27261889/article/details/87284076
- https://blog.csdn.net/algorithmPro/article/details/103982466
- https://blog.csdn.net/weixin_44278406/article/details/105554268
- https://blog.csdn.net/bigFatCat_Tom/article/details/91619977
- https://blog.csdn.net/qq_25737169/article/details/79048516