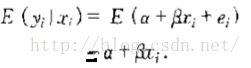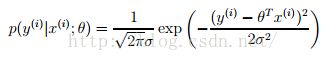统计学习方法(三) logisitic回归与最大熵模型
前言：本文实际为阅读众多LR相关资料总结而成，其中几个讲解得比较好的：
logistic回归--方法与应用
对数线性模型，广义线性模型
在机器学习实战的逻辑斯蒂回归中我们有讲到，logistic模型就是使用sigmoid函数拟合条件概率，具体地：
此前，我的主要理解仅限于sigmoid函数及其函数图像形式。但是为什么使用这个函数来拟合自变量和因变量之间的关系呢？
一.线性回归模型LRM
线性回归模型常用于定量分析中，其限制在于对因变量未做任何限制，这也就引入了假设--因变量y必须在负无穷正无穷之间变化。这就限制了线性回归模型的使用场景---不适用于因变量为分类变量的情况；不适用于因为量在有限区间取值的情况。
对于二分类问题，假设使用线性回归方程：
则其条件期望为：
又由于y只能取值0和1，所以条件期望又等于：
正因如此，因变量为二分类的线性回归模型又称为线性概率模型(Linear Probability Model, 缩写LPM)。
显然，概率取值范围[0, 1]，线性模型不能拟合这种非线性关系，如下图：
二.logistic回归模型LR
自然地，我们想用一个在x趋于负无穷时y趋于零，x趋于正无穷是y趋于1，即值域在[0, 1]之间有着S形状的曲线。这种曲线类似于随机变量的累积分布曲线。常用logistic分布--logistic模型，或者标准正态分布--probit模型。
对LR模型，时间发生于不发生的概率之比(定义为几率，odds)为：
对数几率为：
上述等式右边是线性的，也就是LR模型中，对数线性几率是线性的。所以，LR模型是对数线性模型的特例，后文会介绍的最大熵模型也是对数线性模型。
总结：LR的公式为什么是这个形式？答：简单粗暴的理解就是需要一个上述提到的S型曲线的函数，sigmoid函数符合该形式。还可以从广义线性模型的角度来理解，logistic回归模型假设输出是服从伯努利分布，根据广义线性模型的要求可得其概率形式。具体参见前言中提到的第二个链接。（注：更进一步的理解，可参见ANdrewNg的课程讲义，网址Ng讲义--广义线性回归）
三.线性回归模型VS逻辑斯谛回归
同：LRM的原则也应用于LR
异：两者是完全不同的：
1）LRM中自变量与因变量是线性关系，LR中为非线性；
2）LRM中假设对自变量xi 的某个值，yi的观测值有正太分布；而LR中卫二项分布；
3）LR中不存在LRM中有的残差项
总结来说，为什么在分类问题上使用LR而启用线性回归模型的原因主要有二：
1）等式两边的取值范围不同，右边是负无穷到正无穷，左边是[0,1]，这个分类模型的存在问题
2）实际中的很多问题，都是当x很小或很大时，对于因变量P的影响很小，当x达到中间某个阈值时，影响很大。即实际中很多问题，概率P与自变量并不是直线关系。
为什么在LRM中优化目标函数是最小二乘，而LR中是极大似然函数？
答：逻辑回归中，Y服从二项分布，误差服从二项分布，而非高斯分布，所以不能用最小二乘进行模型参数估计，可以用极大似然估计来进行参数估计。具体而言，线性回归模型满足如下等式：
该模型假设误差(噪声)符号0均值的正态分布，则给定xi 的输出符合正态分布，即：
由于有上式得假设，故而有如下似然函数：
对上述似然函数的最大化实质就是least mean squares。
而对logistic回归，其给定xi 的输出yi 服从二项分布二分正态分布，故最小二乘不适用。
补充@2016.12.01 logistic回归的损失函数是对数损失函数！！！【
对数损失函数 L(Y, P(Y|X)) = -log P(Y|X)】
看到一篇博客，是关于AndrewNg的课程的笔记，当时看那个笔记作为入门还是觉得讲广义线性模型GLM有点难，公式看的宝宝好困。但是现在回过头来看，从一般线性回归到加权线性回归，再到logistic回归，最后是Genralized Linear Model，其实条理真的很清晰。
但是重点是为什么会有GLM这个东西，我还是没很明白~于是乎，尝试去看wiki，【这是一次伟大的尝试，一个良好的开端~~~
首先，理解一下为什么会有GLM：
我们知道一般线性回归是基于噪声是正态分布的假设的，这个假设其实以为着一般线性回归的假设是y在x和噪声的条件下是正态分布的。因此，GLM的扩展在于可以假设噪声是任意分布的。但是它又叫线性模型，为嘛呢？因为输出虽然不再是x的线性，但是y还是g(wx)，也就是原来的线性求和，做一个变换再得到y。
前面在讲logistic回归的时候讲到，不能用线性回归最显著的一个特点就是线性回归y的值域是正无穷到负无穷的，而概率是[0,1]的。再有就是线性回归拟合的是一条直线啊，这就意味着一定量的x的变换一定导致常量的y的变换，但是对很多实际场景，这是不正确的，比如说随着x的增大，x的变化对y的影响变小了。
所以logistic回归有两个解释，一个是对数几率是线性模型，一个是它是伯努利分布下的GLM。
以上，一个GLM由三个部分组成：1）一个属于指数家族的分布；2）一个线性预测器；3）一个映射函数g(z)，由线性组合映射到输出y。
wiki还没看完，to be continued...
补充@2016.12.01
看到一篇博客，是关于AndrewNg的课程的笔记，当时看那个笔记作为入门还是觉得讲广义线性模型GLM有点难，公式看的宝宝好困。但是现在回过头来看，从一般线性回归到加权线性回归，再到logistic回归，最后是Genralized Linear Model，其实条理真的很清晰。
但是重点是为什么会有GLM这个东西，我还是没很明白~于是乎，尝试去看wiki，【这是一次伟大的尝试，一个良好的开端~~~
首先，理解一下为什么会有GLM：
我们知道一般线性回归是基于噪声是正态分布的假设的，这个假设其实以为着一般线性回归的假设是y在x和噪声的条件下是正态分布的。因此，GLM的扩展在于可以假设噪声是任意分布的。但是它又叫线性模型，为嘛呢？因为输出虽然不再是x的线性，但是y还是g(wx)，也就是原来的线性求和，做一个变换再得到y。
前面在讲logistic回归的时候讲到，不能用线性回归最显著的一个特点就是线性回归y的值域是正无穷到负无穷的，而概率是[0,1]的。再有就是线性回归拟合的是一条直线啊，这就意味着一定量的x的变换一定导致常量的y的变换，但是对很多实际场景，这是不正确的，比如说随着x的增大，x的变化对y的影响变小了。
所以logistic回归有两个解释，一个是对数几率是线性模型，一个是它是伯努利分布下的GLM。
以上，一个GLM由三个部分组成：1）一个属于指数家族的分布；2）一个线性预测器；3）一个映射函数g(z)，由线性组合映射到输出y。
补充@2016.12.03
前(fei)言(hua)：宝宝真的是一个热爱学习的勤奋好宝宝~~~
又从另一个思路思考了一下logistic回归，毕竟这个模型效果好，实际中很经常使用嘛，以我少有的面试经验来看，在面试中常常会问到LR。
恩，上面有讲到最小二乘法是线性回归在噪声为正态分布假设下的最大似然估计，然后logistic回归我们就只介绍说它也是用最大似然估计，然后我们是这样推导出theta的更新规则的：
假设对数几率(log odds)是线性分布的【不知道的请自行回去翻统计学习方法，并面壁思过】，然后用最大似然估计推到出了最小化的目标(最大似然)：
![$$J(\theta) = - \frac{1}{m}\left [ \sum_{i=1}^m y^{(i)} \log h_{\theta}(x^{(i)}) + (1-y^{(i)}) \log(1-h_{\theta}(x^{(i)})) \right ]$$](http://img.e-com-net.com/image/info8/029066a01d6f439a891425f40791b421.gif)
后来我们发现，这等同于最小化损失时将损失函数取为对数损失。
总结：在线性回归中损失函数是平方损失，因为其基本假设是噪声符合正态分布，基于此假设用最大似然估计，等同于平方损失和最小化。
在logistic回归中损失函数是对数损失，因为在对数几率为线性的假设下，用最大似然估计，等同于log损失和最小化。log损失形式是 L(Y, P(Y|X)) = -log P(Y|X)