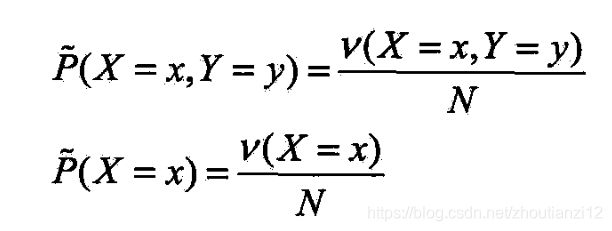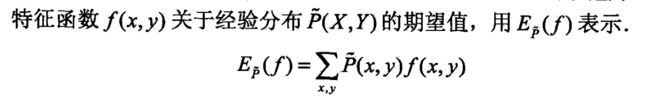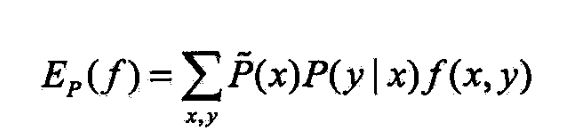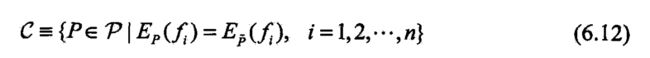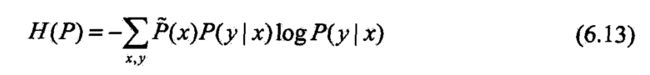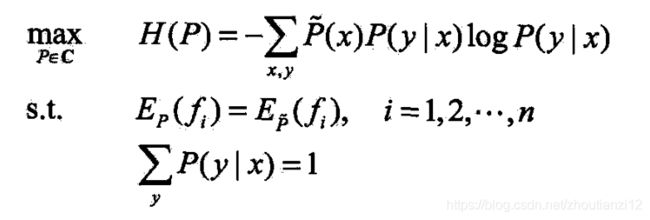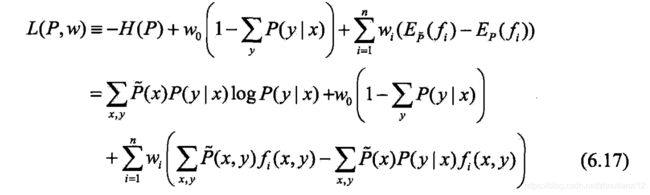6 logistic回归与最大熵模型
文章目录
- 6.1 逻辑斯谛回归模型
- 6.1.1 逻辑斯蒂分布
- 6.1.2 逻辑斯蒂回归模型
- 6.1.3 模型参数估计
- P ( Y = 1 ∣ x ) = π ( x ) , P ( Y = 0 ∣ x ) = 1 ー π ( x ) P(Y=1|x)=\pi(x),P(Y=0|x)=1ー\pi(x) P(Y=1∣x)=π(x),P(Y=0∣x)=1ーπ(x)
- 6.1.4 多项逻辑斯蒂回归
- 6.2 最大熵模型
- 6.2.1 最大熵原理
- 6.2.2最大熵模型的定义
- 6.2.3最大熵模型的学习
- 最大熵是概率模型学习的一个准则,将其推广到分类问题得到maximum entropy model).
- 逻辑斯谛回归与最大熵都属对数线性模型.
- 本章先逻辑斯谛回归模型,然后介绍最大熵模型
- 最后讲述逻辑斯谛回归与最大熵模型的学习算法,
- 包括改进的迭代尺度算法和拟牛顿法
6.1 逻辑斯谛回归模型
6.1.1 逻辑斯蒂分布
-
definition 6.1
-
X X X连续随机变量
F ( x ) = P ( X ≤ x ) = 1 1 + e − ( x − μ ) / γ (6.1) F(x)=P(X\le x)=\frac{1}{1+e^{-(x-\mu)/\gamma}}\tag{6.1} F(x)=P(X≤x)=1+e−(x−μ)/γ1(6.1)
f ( x ) = e − ( x − μ ) / γ γ ( 1 + e − ( x − μ ) / γ ) 2 (6.2) f(x)=\frac{e^{-(x-\mu)/\gamma}}{\gamma(1+e^{-(x-\mu)/\gamma})^2}\tag{6.2} f(x)=γ(1+e−(x−μ)/γ)2e−(x−μ)/γ(6.2) -
位参
-
形参
- F F F属逻辑斯谛函数
- S形曲线( sigmoid curve)
- ( μ , 1 2 ) (\mu,\frac 12) (μ,21)为中心对称
f ( − x + μ ) − 1 2 = − F ( x − μ ) + 1 2 f(-x+\mu)-\frac 12=-F(x-\mu)+\frac 12 f(−x+μ)−21=−F(x−μ)+21
- 形参 γ \gamma γ越小,曲线在中心附近增长得越快
6.1.2 逻辑斯蒂回归模型
- binomial logistic regression model是一种分类模型,
- 由条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)表示,形式为参数化的逻辑斯谛分布.
- X取实数,Y1或0.
- 二项逻辑斯谛回归模型是如下的条件概率分布
P ( Y = 1 ∣ x ) = e x p ( w ⋅ x + b ) 1 + e x p ( w ⋅ x + b ) (6.3) P(Y=1|x)=\frac{exp(w\cdot x+b)}{1+exp(w\cdot x+b)}\tag{6.3} P(Y=1∣x)=1+exp(w⋅x+b)exp(w⋅x+b)(6.3)
P ( Y = 0 ∣ x ) = 1 1 + e x p ( w ⋅ x + b ) (6.4) P(Y=0|x)=\frac{1}{1+exp(w\cdot x+b)}\tag{6.4} P(Y=0∣x)=1+exp(w⋅x+b)1(6.4)
- 将权值向量和输入向量扩充,仍记作 w w w, x x x,
- 即 w = ( w ( 1 ) , w ( 2 ) , … , w ( n ) , b ) w=(w^{(1)},w^{(2)},…,w^{(n)},b) w=(w(1),w(2),…,w(n),b)
- x = ( x ( 1 ) , x ( 2 ) , … , 1 , ) x=(x^{(1)},x^{(2)},…,1,) x=(x(1),x(2),…,1,)
- 这时,模型如下
P ( Y = 1 ∣ x ) = e x p ( w ⋅ x ) 1 + e x p ( w ⋅ x ) (6.5) P(Y=1|x)=\frac{exp(w\cdot x)}{1+exp(w\cdot x)}\tag{6.5} P(Y=1∣x)=1+exp(w⋅x)exp(w⋅x)(6.5)
P ( Y = 0 ∣ x ) = 1 1 + e x p ( w ⋅ x ) (6.6) P(Y=0|x)=\frac{1}{1+exp(w\cdot x)}\tag{6.6} P(Y=0∣x)=1+exp(w⋅x)1(6.6)
- 事件的几率(odds)
- 指该事件发生的概率与不发生的比值
- 发生是P,则事件几率是 p 1 − p \frac {p}{1-p} 1−pp
- 该事件的对数几率( log odds)或logit是
l o g i t ( p ) = l o g p 1 − p logit(p)=log \frac{p}{1-p} logit(p)=log1−pp
- 该事件的对数几率( log odds)或logit是
- 对逻辑斯谛回归而言,由(6.5)与(6.6)得
l o g P ( Y = 1 ∣ x ) 1 − P ( Y = 1 ∣ x ) = w ⋅ x log \frac{P(Y=1|x)}{1-P(Y=1|x)}=w\cdot x log1−P(Y=1∣x)P(Y=1∣x)=w⋅x - 输出 Y = 1 Y=1 Y=1的对数几率是输入 x x x的线性函数.
- 输出 Y = 1 Y=1 Y=1的对数几率是由输入 x x x的线性函数
- 表示的模型,
- 就是逻辑斯谛回归模型
- 对输入 x x x进行分类的线性函数 w ⋅ x w\cdot x w⋅x,值域为实数.
- x ∈ R n + 1 x\in R^{n+1} x∈Rn+1
- w ∈ R n + 1 w\in R^{n+1} w∈Rn+1
- 通过逻辑斯谛回归模型定义(6.5)可将线性函数 w ⋅ x w\cdot x w⋅x转换为概率
P ( Y = 1 ∣ x ) = e x p ( w ⋅ x ) 1 + e x p ( w ⋅ x ) P(Y=1|x)=\frac{exp(w\cdot x)}{1+exp(w\cdot x)} P(Y=1∣x)=1+exp(w⋅x)exp(w⋅x)
- 线性函数的值越近 + ∞ +\infty +∞,概率就越近1;
- 线性函数的值越近 − ∞ -\infty −∞,概率就越近0
- (如图6.1).
- 这样的模型就是逻辑斯谛回归模型
6.1.3 模型参数估计
- 训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x N , y N ) } T=\{(x_1,y_1),(x_2,y_2),…,(x_N,y_N)\} T={(x1,y1),(x2,y2),…,(xN,yN)},
- 用极大似然估计法估计参数
P ( Y = 1 ∣ x ) = π ( x ) , P ( Y = 0 ∣ x ) = 1 ー π ( x ) P(Y=1|x)=\pi(x),P(Y=0|x)=1ー\pi(x) P(Y=1∣x)=π(x),P(Y=0∣x)=1ーπ(x)
- 似然函数为
∏ i = 1 N [ π ( x i ) ] y i [ 1 − π ( x i ) ] 1 − y i \prod_{i=1}^N[\pi(x_i)]^{y_i}[1-\pi(x_i)]^{1-y_i} i=1∏N[π(xi)]yi[1−π(xi)]1−yi - 对数似然函数为
L ( w ) = ∑ i = 1 N [ y i l o g π ( x i ) + ( 1 − y i ) l o g ( 1 − π ( x i ) ) ] L(w)=\sum_{i=1}^N[y_ilog\pi(x_i)+(1-y_i)log(1-\pi(x_i))] L(w)=i=1∑N[yilogπ(xi)+(1−yi)log(1−π(xi))]
= ∑ i = 1 N [ y i l o g π ( x i ) 1 − π ( x i ) + l o g ( 1 − π ( x i ) ) ] =\sum_{i=1}^N[y_ilog\frac{\pi(x_i)}{1-\pi(x_i)}+log(1-\pi(x_i))] =i=1∑N[yilog1−π(xi)π(xi)+log(1−π(xi))]
∑ i = 1 N [ y i ( w ⋅ x i ) − l o g ( 1 + e x p ( w ⋅ x i ) ) ] \sum_{i=1}^N[y_i(w\cdot x_i)-log(1+exp(w\cdot x_i))] i=1∑N[yi(w⋅xi)−log(1+exp(w⋅xi))] - 对 L ( w ) L(w) L(w)求极大值,得 w w w的估计值
- 问题变成了以对数似然函数为目标函数的最优化问题,
- 逻辑斯谛回归学习中常用
- 是梯度下降法及
- 拟牛顿法
- 设 w w w的极大似然估计值是 w ^ \hat{w} w^,
- 则学到的逻辑斯谛回归模型为
6.1.4 多项逻辑斯蒂回归
-
上介绍二分类
-
可将其推广multi-nominal logistic regression model,
-
设 Y Y Y的取值是 1 , 2 , . . . , K 1,2,...,K 1,2,...,K
-
多项逻辑斯谛回归模型
P ( Y = k ∣ x ) = e x p ( w k ⋅ x ) 1 + ∑ k = 1 K − 1 e x p ( w k ⋅ x ) k = 1 , 2 , . . . , K − 1 P(Y=k|x)=\frac{exp(w_k\cdot x)}{1+\sum_{k=1}^{K-1}exp(w_k\cdot x)}k=1,2,...,K-1 P(Y=k∣x)=1+∑k=1K−1exp(wk⋅x)exp(wk⋅x)k=1,2,...,K−1
P ( Y = K ∣ x ) = 1 1 + ∑ k = 1 K − 1 e x p ( w k ⋅ x ) P(Y=K|x)=\frac{1}{1+\sum_{k=1}^{K-1}exp(w_k\cdot x)} P(Y=K∣x)=1+∑k=1K−1exp(wk⋅x)1 -
x ∈ R n + 1 x\in R^{n+1} x∈Rn+1
-
w k ∈ R n + 1 w_k\in R^{n+1} wk∈Rn+1
-
二项逻辑斯谛回归的参数估计法
- 可推广到多项.
6.2 最大熵模型
- maximum entropy model由最大熵原理推导实现
- 先 一般的最大熵原理,
- 然 最大熵模型的推导,
- 最 最大熵模型学习的形式
6.2.1 最大熵原理
- 谁是概率模型学习的一个准则.
- 它认为,学习概率模型时在所有可能的概率模型(分布)中,
- 熵最大的模型是最好的.
- 用约束条件来确定概率模型的集合,
- 所以,最大熵原理可表述为
- 在满足约束条件的模型集合
- 中选熵最大的.
- 离散随变 X X X的概率分布 P ( X ) P(X) P(X),
- 其熵(参5.2.2)是
H ( P ) = − ∑ x P ( x ) l o g P ( x ) (6.9) H(P)=-\sum_xP(x)logP(x)\tag{6.9} H(P)=−x∑P(x)logP(x)(6.9)
0 ≤ H ( P ) ≤ l o g ∣ X ∣ 0\le H(P)\le log|X| 0≤H(P)≤log∣X∣
- ∣ X ∣ |X| ∣X∣是 X X X的取值个数,
- 当且仅当X的是均匀分布时等号成立
- 均匀分布时,熵最大.
- 谁认为要选的概率模型必先满足事实
- 即约束
- 无更多信息情况下,不确定的部分“等可能”
- 最大熵原理通过熵的最大化表示等可能
- “等可能”不易操作,
- 熵则是可优化的数值
- 例子来介绍最大熵原理
- 例6.1
- 随机变量 X X X有5取值${A,B,C,D,E}$
- 估计取各个值的概率P
-
解
-
概率值满足约束
P ( A ) + P ( B ) + P ( C ) + P ( D ) + P ( E ) = 1 P(A)+P(B)+P(C)+P(D)+P(E)=1 P(A)+P(B)+P(C)+P(D)+P(E)=1 -
满足此约束的概率分布无穷多.
-
若无其他信息,仍要对概率估计,
- 一法是认为这个分布中取各个值是相等
- 为1/5
- 等概率表示了对事实的无知,
- 因为无多信息,此判断合理
- 有时从先验知识中得到对概率值的约束,
- 如:
P ( A ) + P ( B ) = 3 10 P(A)+P(B)=\frac{3}{10} P(A)+P(B)=103
P ( A ) + P ( B ) + P ( C ) + P ( D ) + P ( E ) = 1 P(A)+P(B)+P(C)+P(D)+P(E)=1 P(A)+P(B)+P(C)+P(D)+P(E)=1 - 满足这两约束的概率仍无穷多
- 在缺少其他信息的情况下
- 可认为A、B等概率
- C,D与E等概率
- 若还有约束:
P ( A ) + P ( C ) = 1 2 P(A)+P(C)=\frac 12 P(A)+P(C)=21
P ( A ) + P ( B ) = 3 10 P(A)+P(B)=\frac {3}{10} P(A)+P(B)=103
( A ) + P ( B ) + P ( C ) + P ( D ) + P ( E ) = 1 (A)+P(B)+P(C)+P(D)+P(E)=1 (A)+P(B)+P(C)+P(D)+P(E)=1 - 可继续按约束条件下求等概率的方法估计概率分布.
- 这里不讨论.
- 以上概率模型学习的方法正遵循了最大熵原理
-
图6.2提供用最大熵原理进行概率模型选择的几何解释
-
概率模型集合 P P P可由欧氏空间中的simplex表示
- 如左图的三角形(2-单纯形).
-
一个点代表一个模型,整个单纯形代表模型集合
- 右图上的一条直线对应一个约束,
- 直线的交集对应满足所有约束的模型集合
- 一般地,这样的模型有无穷多
-
学习的目的是在可能的模型集合中选择最优模型,
- 最大熵原理给出最优模型选择的一准则
-
单纯形是在m维欧氏空间中的n+1个仿射无关的点的集合的凸包
6.2.2最大熵模型的定义
- 最大熵原理是统计学习的一般原理,
- 应用到分类得最大熵模型
- 设分类模型是条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X),
- X ∈ X ⊆ R n X\in\mathcal{X}\subseteq R^{n} X∈X⊆Rn表示输入,
- Y ∈ Y Y\in\mathcal{Y} Y∈Y表输出
- 模型表示的是对给定输入 X X X,
- 以条件概率输出 Y Y Y
- 给定
- 学习的目标是用最大熵原理选最好的分类模型
- 首先考虑模型应该满足的条件.
- 给定训练数据集,可确定联合分布 P ( X , Y ) P(X,Y) P(X,Y)的经验分布和
- 边缘分布 P ( X ) P(X) P(X)的经验分布,分别以啥和啥表示
- 特征函数 f ( x , y ) f(x,y) f(x,y)描述输入 x x x和输出 y y y间的某一个事实
- 一般特征函数可是任意实函数
- 特征函数关于模型 P ( Y ∣ X ) P(Y|X) P(Y∣X)与经验分布 p ~ ( X ) \tilde{p}(X) p~(X)产的期望值,
- 如果模型能获取训练数据中的信息,
- 就可假设这两个期望值相等,
- 即
- 将式(6.10)或式(6.11)作为模型学习的约束条件.
- 假如有n个特征函数
- 那就有n个约東条件
- 定义6.3(最大熵模型)
- 设满足所有约東条件的模型集合为
- 定义在条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)上的条件熵为
- 则模型集合 C C C中条件熵 H ( P ) H(P) H(P)最大的模型称为最大嫡模型.
- 为自然对数
6.2.3最大熵模型的学习
- 最大熵模型的学习过程就是求解最大熵模型的过程.
- 最大熵模型的学习可以形式化为
- 约朿最优化问题
- 对给定的训练数据集及特征函数
- 最大熵模型的学习等价于约束最优化问题
- 将求最大值问题改写为等价的求最小值问题
- (6.14)~(6.16)的解,
- 就是最大熵模型学习的解.
- 下面推导
- 这里将约束最优化的原始问题转换为无约束最优化的对偶问题
- 通过求解对偶问题求解原始问题
- 引进拉格朗日乘子 w 0 , w 1 , . . . , w n w_0,w_1,...,w_n w0,w1,...,wn
- 定义拉格朗日函数 L ( P , w ) L(P,w) L(P,w)
- 最优化的原始问题是
- 对偶问题是
写到这儿了