模拟退火算法的 C++ 实现
模拟退火算法的 C++ 实现
最近的一个项目中需要实现个路径规划的算法,需要求得的路径的总长度尽可能的短。这就是典型的旅行商(TSP)问题了。解决这个问题的一个比较好用的方法就是模拟退火算法。网上关于用模拟退火算法解决 TSP 问题的文章挺多的,其中也有不少号称给出了 C++ 代码。但是说句实话,这些代码中没有一个是按照面向对象的思想来实现了,并没有把模拟退火算法的框架封装好。因此,遇到一个新问题时,改写算法就很麻烦。
看了几个网上的实现后,发现 gsl 库给出的框架还是不错的。但是 gsl 是 C 语言的库,虽然是按照面向对象的思想来设计的,但是实现的接口真是挺繁琐的,用起来并不好用。因此,我就花了半天时间,把 gsl 里的相关代码扒了出来,重新封装到了一个类中。
模拟退火算法最早的思想是由 Metropolis 等人提出的。1983 年, Kirkpatrick 成功地将退火思想引入到组合优化领域。简单的说,模拟退火算法就是一种基于 Monte-Carlo 迭代求解策略的随机寻优算法。关于模拟退火算法的理论网上有很多文章介绍。这里就不多写了,今天主要说说如何C++ 实现。
模拟退火算法的核心功能封装到了 SimulatedAnnualingSolver 类中。
#ifndef SIMULATEDANNUALINGSOLVER_H
#define SIMULATEDANNUALINGSOLVER_H
#include#include "SimulatedAnnualingSolver.h"
#include 这个类有几个纯虚函数。
- take_step 用来在解空间中随机游走到一个新的状态。
- undo_step 撤销最近的一次游走。
- save_best 将当前的状态保存下来,最为当前最佳的解。
- energy 能量函数,返回当前状态的目标函数值。(模拟退火算法就是求这个能量函数最小值所对应的状态)
- print 输出当前状态。这个函数只是起辅助作用,如果不需要,可以实现为空函数。
对于我们一个具体的问题,我们只需要定义一个派生自这个类的新类,在新类中实现这些虚函数。
比如对于我的问题,一个简化了的旅行商问题,我建立了一个 TspSolver 的类。
#ifndef TSPSOLVER_H
#define TSPSOLVER_H
#include "SimulatedAnnualingSolver.h"
#include points);
QVector result();
protected:
double take_step(double step_size) override;
void undo_step() override;
void save_best() override;
double energy() override;
void print() override;
private:
std::mt19937 m_randGen;
QVector m_points;
QVector m_best;
int m_N;
int m_n1;
int m_n2;
};
#endif // TSPSOLVER_H
#include "tspsolver.h"
tspSolver::tspSolver(int rand_seed, QVector points)
:SimulatedAnnualingSolver(rand_seed)
{
std::random_device r;
std::seed_seq seed2{r(), r(), r(), r(), r(), r(), r(), r()};
m_randGen.seed(seed2);
m_points = points;
m_N = m_points.size();
}
void tspSolver::save_best()
{
m_best = m_points;
}
QVector tspSolver::result()
{
return m_best;
}
void tspSolver::print()
{
qDebug() << m_points;
}
double tspSolver::take_step(double step_size)
{
std::uniform_int_distribution<> dis(1, m_N - 1);
m_n1 = dis(m_randGen);
do
{
m_n2 = dis(m_randGen);
}
while(m_n2 == m_n1);
// qDebug() << "n1 = " << m_n1 << "n2 = " << m_n2;
std::swap(m_points[m_n1], m_points[m_n2]);
return energy();
}
void tspSolver::undo_step()
{
std::swap(m_points[m_n1], m_points[m_n2]);
}
double tspSolver::energy()
{
double e = 0;
for(int i = 1; i < m_N; i ++)
{
QPoint a1 = m_points.at(i - 1);
QPoint a2 = m_points.at(i);
double x = abs(a1.x() - a2.x());
double y = abs(a1.y() - a2.y());
e += qMax(x, y);
}
return e;
} 大家可以看到,我这个 TSP 问题中的两点间的距离不是普通的直线距离,而是 X Y 方向投影距离的最大值。
take_step 函数实现的也很简答,就是随机选两个点,交换这两个点的坐标。undo_step 就是把这两个点的坐标再交换回去。
下面是一个算例,随便选了 9 个点。规划出的路径看起来还不错。
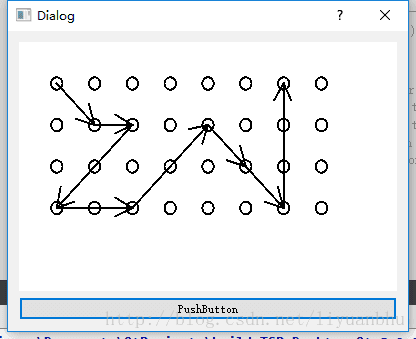
这个算例选了 32 个点。规划出的路径挺复杂,但是每一步的长度都是 1,所以是最优解。当然这个问题的最优解不止一个。这里得到的解是最优解中较复杂的一个情形。
