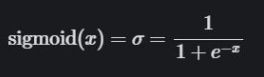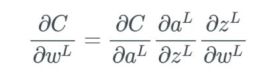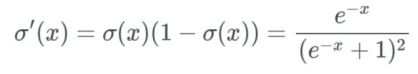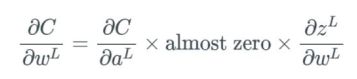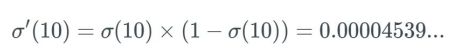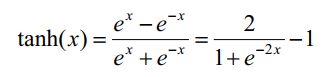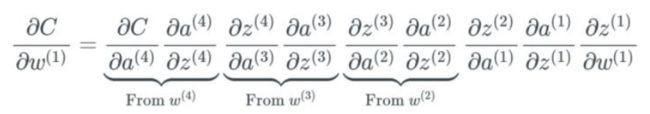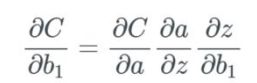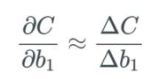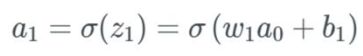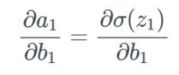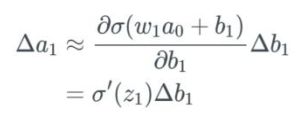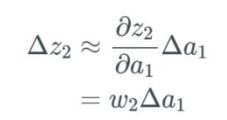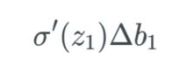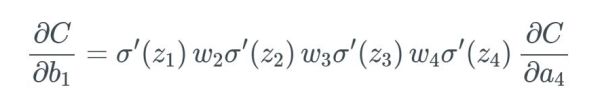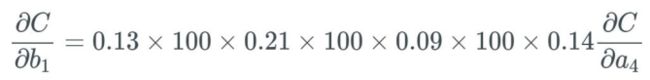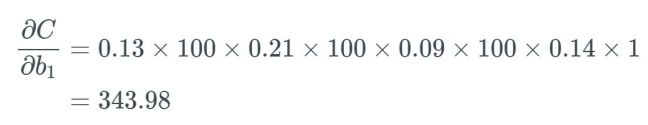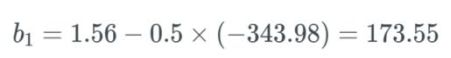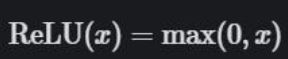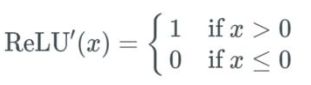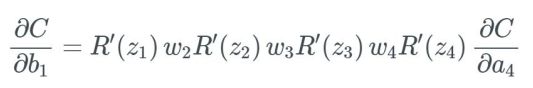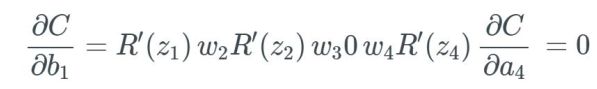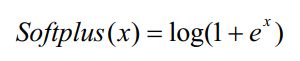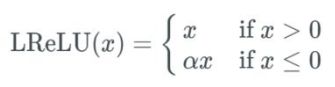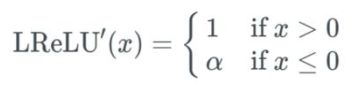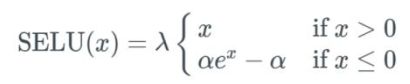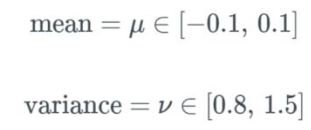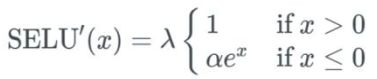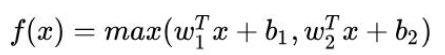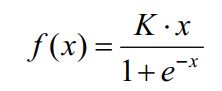【深度学习】2、Pytorch自行实现常见的11个激活函数的Fashion Minist项目实践对比（你需要的这里都有了！）

简介

神经网络为什么需要激活函数：首先数据的分布绝大多数是非线性的，而一般神经网络的计算是线性的，引入激活函数，是在神经网络中引入非线性，强化网络的学习能力。所以激活函数的最大特点就是非线性。

    激活函数对神经网络的重要性自不必多言，来自丹麦技术大学的 Casper Hansen 通过公式、图表和代码实验介绍了 Sigmoid、Tanh、ReLU、Softplus、Softmax、ELU 以及更新的 Leaky ReLU、SELU、GELU、Maxout 以及Swish这些激活函数，并比较了它们的优势和短板。

    在计算每一层的激活值时，我们要用到激活函数，之后才能确定这些激活值究竟是多少。根据每一层前面的激活、权重和偏置，我们要为下一层的每个激活计算一个值。但在将该值发送给下一层之前，我们要使用一个激活函数对这个输出进行缩放。本文将介绍不同的激活函数。

 

1、概述

    激活函数是神经网络中一个至关重要的部分。在这篇长文中，我将全面介绍11种不同的激活函数，并阐述它们各自的优缺点。我会给出激活函数的方程和微分方程，还会给出它们的图示。本文的目标是以简单的术语解释这些方程以及图。

 

2、Sigmoid 函数

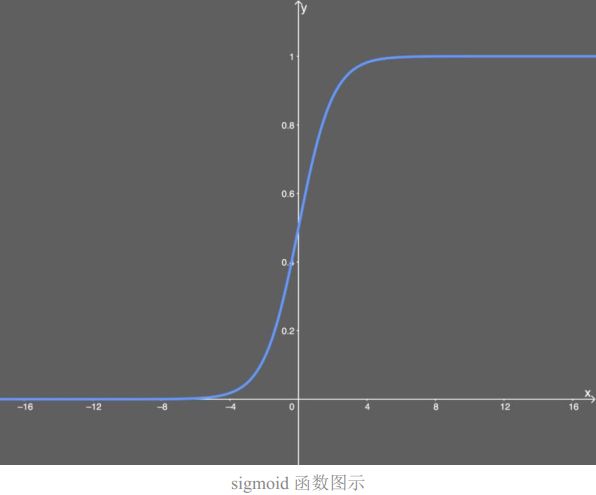
    Sigmoid 函数是一个Logistic函数，意思就是说：不管输入是什么，得到的输出都在0到1之间。也就是说，你输入的每个神经元、节点或激活都会被缩放为一个介于 0到1之间的值。

    ​sigmoid 这样的函数常被称为非线性函数，因为我们不能用线性的项来描述它。很多激活函数都是非线性或者线性和非线性的组合（有可能函数的一部分是线性的，但这种情况很少见）。

    ​这基本上没什么问题，但值恰好为 0 或 1 的时候除外（有时候确实会发生这种情况）。为什么这会有问题？

    ​这个问题与反向传播有关（有关反向传播的介绍请参阅我的前一篇文章）。在反向传播中，我们要计算每个权重的梯度，即针对每个权重的小更新。这样做的目的是优化整个网络中激活值的输出，使其能在输出层得到更好的结果，进而实现对成本函数的优化。

    ​在反向传播过程中，我们必须计算每个权重影响成本函数（cost function）的比例，具体做法是计算成本函数相对于每个权重的偏导数。假设我们不定义单个的权重，而是将最后一层 L 中的所有权重 w 定义为 w^L，则它们的导数为:

    ​注意，当求偏导数时，我们要找到 ∂a^L 的方程，然后仅微分 ∂z^L，其余部分保持不变。我们用撇号「'」来表示任意函数的导数。当计算中间项 ∂a^L/∂z^L 的偏导数时，我们有：

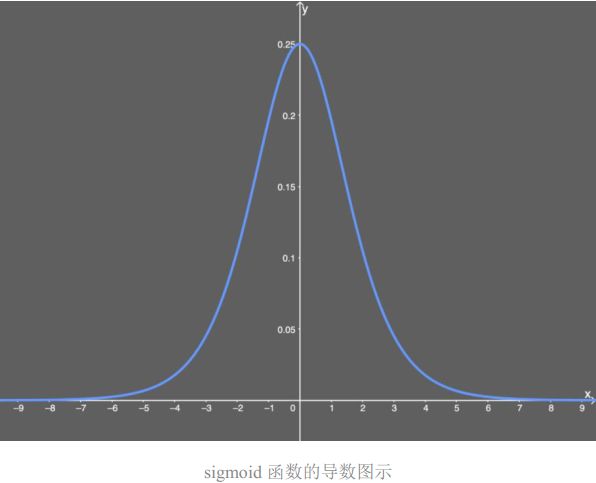
    ​则sigmoid 函数的导数就为：

    当我们向这个 sigmoid 函数输入一个很大的x值（正或负）时，我们得到几乎为 0 的y值——也就是说，当我们输入 w×a+b 时，我们可能得到一个接近于 0 的值。

    ​当 x 是一个很大的值（正或负）时，我们本质上就是用一个几乎为0的值来乘这个偏导数的其余部分。

    ​如果有太多的权重都有这样很大的值，那么我们根本就没法得到可以调整权重的网络，这可是个大问题。如果我们不调整这些权重，那么网络就只有细微的更新，这样算法就不能随时间给网络带来多少改善。对于针对一个权重的偏导数的每个计算，我们都将其放入一个梯度向量中，而且我们将使用这个梯度向量来更新神经网络。可以想象，如果该梯度向量的所有值都接近 0，那么我们根本就无法真正更新任何东西。

    这里描述的就是梯度消失问题。这个问题使得 sigmoid 函数在神经网络中并不实用，我们应该使用后面介绍的其它激活函数。

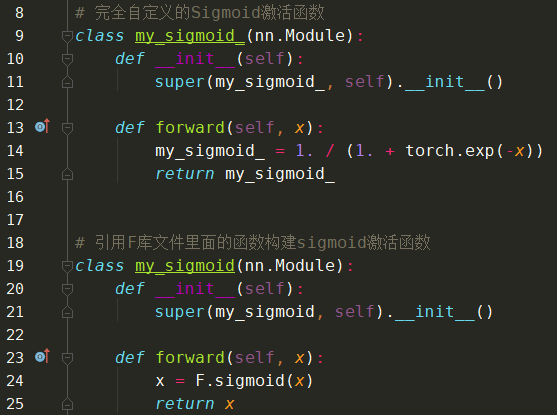
Sigmoid函数的自定义实现：

 

3、Tanh函数

    tanh为双曲正切函数，其英文读作Hyperbolic Tangent。tanh和 sigmoid 相似，都属于饱和激活函数，区别在于输出值范围由 (0,1) 变为了 (-1,1)，可以把 tanh 函数看做是 sigmoid 向下平移和拉伸后的结果。

tanh公式：

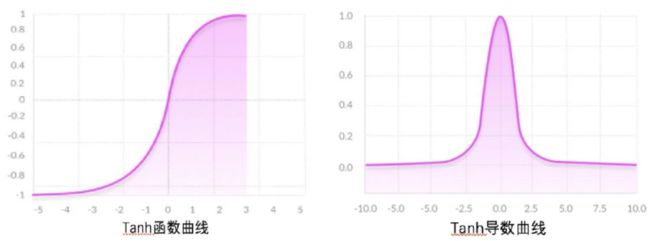
    从公式中，可以更加清晰看出tanh与sigmoid函数的关系（平移+拉伸）。tanh及其导数曲线：

tanh作为激活函数的特点：

相比Sigmoid函数，

    1、tanh的输出范围时(-1, 1)，解决了Sigmoid函数的不是zero-centered输出问题；

    2、幂运算的问题仍然存在；

    3、tanh导数范围在(0, 1)之间，相比sigmoid的(0, 0.25)，梯度消失（gradient vanishing）问题会得到缓解，但仍然还会存在。

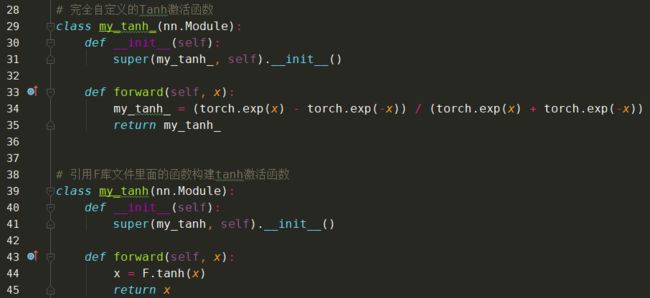
自定义实现：

 

4、梯度问题

4.1、梯度消失问题

 

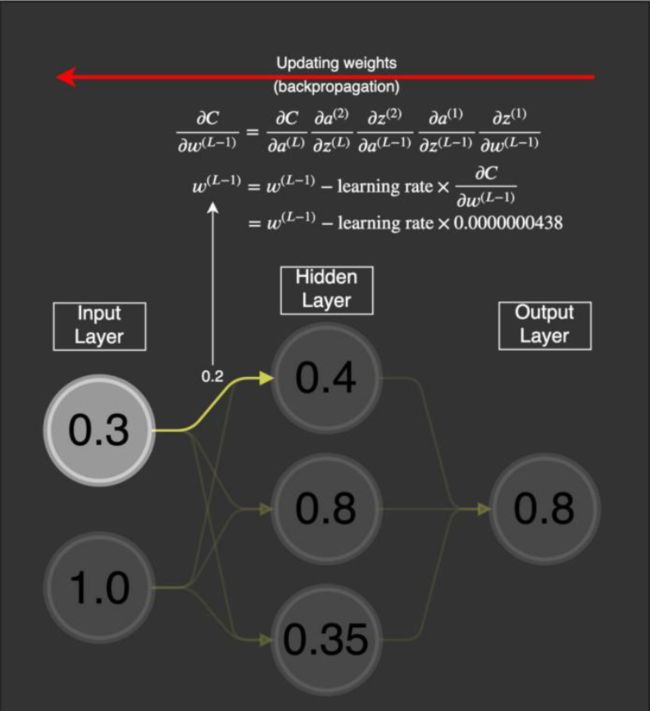
更新特定的权重，则更新规则为：

    但如果偏导数 ∂C/∂w^(L) 很小，如同消失了一般，又该如何呢？这时我们就遇到了梯度消失问题，其中许多权重和偏置只能收到非常小的更新。

    可以看到，如果权重的值为 0.2，则当出现梯度消失问题时，这个值基本不会变化。因为这个权重分别连接了第一层和第二层的首个神经元：

    假设这个权重的值为 0.2，给定一个学习率（具体多少不重要，这里使用了 0.5），则新的权重为：

    这个权重原来的值为 0.2，现在更新为了 0.199999978。很明显，这是有问题的：梯度很小，如同消失了一样，使得神经网络中的权重几乎没有更新。这会导致网络中的节点离其最优值相去甚远。这个问题会严重妨碍神经网络的学习。

 

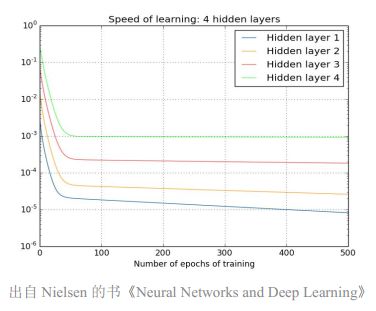
 人们已经观察到，如果不同层的学习速度不同，那么这个问题还会变得更加严重。层以不同的速度学习，前面几层总是会根据学习率而变得更差。

    在这个示例中，隐藏层 4 的学习速度最快，因为其成本函数仅取决于连接到隐藏层 4 的权重变化。我们看看隐藏层 1；这里的成本函数取决于连接隐藏层 1 与隐藏层 2、3、4 的权重变化。如果你看过了我前一篇文章中关于反向传播的内容，那么你可能知道网络中更前面的层会复用后面层的计算。

同时，如前面介绍的那样，最后一层仅取决于计算偏导时出现的一组变化：

    最终，这就是个大问题了，因为现在权重层的学习速度不同。这意味着网络中更后面的层几乎肯定会被网络中更前面的层受到更多优化。而且问题还在于反向传播算法不知道应该向哪个方向传递权重来优化成本函数。

 

4.2、梯度爆炸问题

    ​梯度爆炸问题本质上就是梯度消失问题的反面。研究表明，这样的问题是可能出现的，这时权重处于「爆炸」状态，即它们的值快速增长。

 我们将遵照以下示例来进行说明：http://neuralnetworksanddeeplearning.com/chap5.html#what's_causing_the_vanishing_gradient_problem_unstable_gradients_in_deep_neural_nets

    ​注意，这个示例也可用于展示梯度消失问题，而我是从更概念的角度选择了它，以便更轻松地解释。

    ​本质上讲，当 01 时，我们可能遇到梯度爆炸问题。但是，当一个层遇到这个问题时，必然有更多权重满足梯度消失或爆炸的条件。

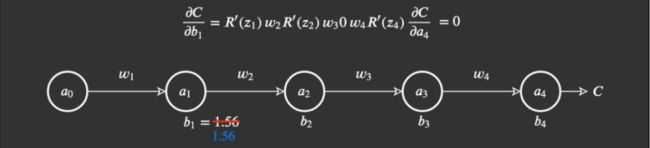
    ​我们从一个简单网络开始。这个网络有少量权重、偏置和激活，而且每一层也只有一个节点。

    这个网络很简单。权重表示为 w_j，偏置为 b_j，成本函数为 C。节点、神经元或激活表示为圆圈。

    Nielsen 使用了物理学上的常用表示方式 Δ 来描述某个值中的变化（这不同于梯度符号 ∇）。举个例子，Δb_j 描述的是第 j 个偏置的值变化。

通过下式衡量变化率：

    下面式子的论据和上面的偏导一样。即我们如何通过偏置的变化率来衡量成本函数的变化率？正如刚才介绍的那样，Nielsen 使用Δ来描述变化，因此我们可以说这个偏导能大致通过Δ来替代：

    先从网络的起点开始，计算第一个偏置 b_1 中的变化将如何影响网络。因为我们知道，在上一篇文章中，第一个偏置 b_1 会馈入第一个激活 a_1，我们就从这里开始。我们先回顾一下这个等式：

    ​如果 b_1 改变，我们将这个改变量表示为 Δb_1。因此，我们注意到当 b_1改变时，激活a_1也会改变——我们通常将其表示为 ∂a_1/∂b_1。

    ​因此，我们左边有偏导的表达式，这是 b_1中与 a_1 相关的变化。但我们开始替换左边的项，先用 z_1 的 sigmoid 替换a_1：

    ​上式表示当 b_1 变化时，激活值 a_1 中存在某个变化。我们将这个变化描述为 Δa_1。

    ​我们将变化 Δa_1 看作是与激活值 a_1 中的变化加上变化 Δb_1 近似一样。

    这里我们跳过了一步，但本质上讲，我们只是计算了偏导数，并用偏导的结果替代了分数部分。a_1 的变化导致 z_2 的变化所描述的变化 Δa_1 现在会导致下一层的输入 z_2 出现变化。

表示方式和前面一样，我们将下一个变化记为 Δz_2。我们又要再次经历前面的过程，只是这次要得到的是 z_2 中的变化：

可以使用下式替代 Δa_1：

​    ​计算这个式子。希望你清楚地明白到这一步的过程——这与计算 Δa_1 的过程一样。

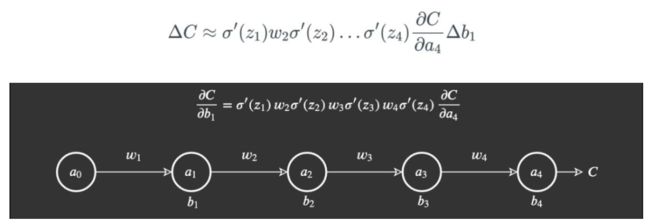
    ​这个过程会不断重复，直到我们计算完整个网络。通过替换 Δa_j 值，我们得到一个最终函数，其计算的是成本函数中与整个网络（即所有权重、偏置和激活）相关的变化。

基于此，我们再计算 ∂C/∂b_1，得到我们需要的最终式：

 

4.3、梯度爆炸的极端案例

    据此，如果所有权重 w_j 都很大，即如果很多权重的值大于 1，我们就会开始乘以较大的值。举个例子，所有权重都有一些非常高的值，比如 100，而我们得到一些在 0 到 0.25 之间、sigmoid 函数导数的随机输出：

可以合理地相信这会远大于1，但为了方便示例展示，我们将其设为 1。

使用这个更新规则，如果我们假设 b_1 之前等于 1.56，而学习率等于 0.5。

尽管这是一个极端案例，但你懂我的意思。权重和偏置的值可能会爆发式地增大，进而导致整个网络爆炸。

    现在花点时间想想网络的权重和偏置以及激活的其它部分，爆炸式地更新它们的值。这就是我们所说的梯度爆炸问题。很显然，这样的网络学不到什么东西，因此这会完全毁掉你想要解决的任务。

 

4.4、避免梯度爆炸：梯度裁剪/规范

    解决梯度爆炸问题的基本思路就是为其设定一个规则。这部分我不会深入进行数学解释，但我会给出这个过程的步骤：

    选取一个阈值——如果梯度超过这个值，则使用梯度裁剪或梯度规范；

    定义是否使用梯度裁剪或规范。如果使用梯度裁剪，你就指定一个阈值，比如 0.5。如果这个梯度值超过 0.5 或 -0.5，则要么通过梯度规范化将其缩放到阈值范围内，要么就将其裁剪到阈值范围内。

     但是要注意，这些梯度方法都不能避免梯度消失问题。所以我们还将进一步探索解决这个问题的更多方法。通常而言，如果你在使用循环神经网络架构（比如 LSTM 或 GRU），那么你就需要这些方法，因为这种架构常出现梯度爆炸的情况

 

5、整流线性单元（ReLU）

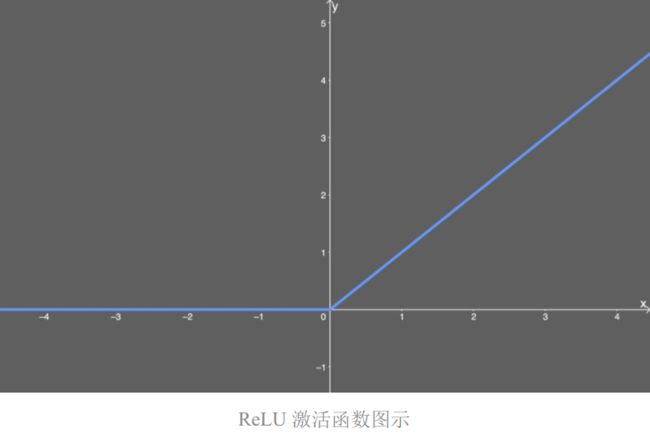
   整流线性单元是我们解决梯度消失问题的方法，但这是否会导致其它问题呢？请往下看。ReLU 的公式如下：

    ​ReLU 公式表明：如果输入 x 小于 0，则令输出等于 0；如果输入 x 大于 0，则令输出等于输入。

    ​尽管我们没法用大多数工具绘制其图形，但你可以这样用图解释 ReLU。x 值小于零的一切都映射为 0 的 y 值，但 x 值大于零的一切都映射为它本身。也就是说，如果我们输入 x=1，我们得到 y=1。

    ​这很好，但这与梯度消失问题有什么关系？首先，我们必须得到其微分方程：

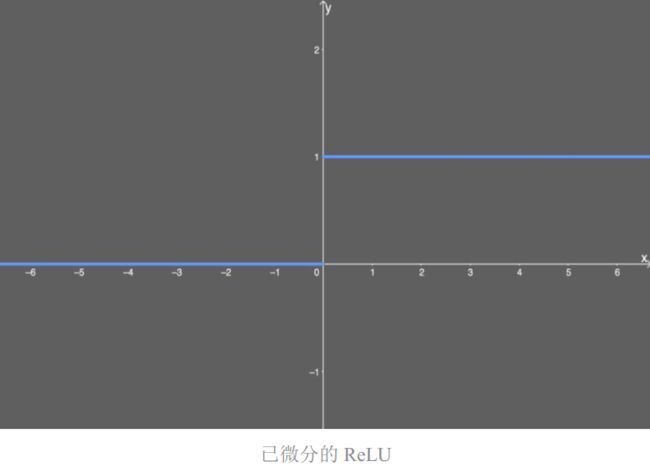
    其意思是：如果输入 x 大于 0，则输出等于 1；如果输入小于或等于 0，则输出变为 0。用下图表示：

    现在我们得到了答案：当使用 ReLU 激活函数时，我们不会得到非常小的值（比如前面sigmoid函数的 0.0000000438）。相反，它要么是0（导致某些梯度不返回任何东西），要么是 1。但这又催生出另一个问题：死亡 ReLU 问题。

    如果在计算梯度时有太多值都低于0会怎样呢？我们会得到相当多不会更新的权重和偏置，因为其更新的量为 0。要了解这个过程的实际表现，我们反向地看看前面梯度爆炸的示例。

我们在这个等式中将ReLU 记为R，我们只需要将每个 sigmoidσ 替换成 R：

现在，假如说这个微分后的 ReLU 的一个随机输入 z 小于 0——则这个函数会导致偏置「死亡」。假设是 R'(z_3)=0：

    反过来，当我们得到 R'(z_3)=0 时，与其它值相乘自然也只能得到 0，这会导致这个偏置死亡。我们知道一个偏置的新值是该偏置减去学习率减去梯度，这意味着我们得到的更新为 0。

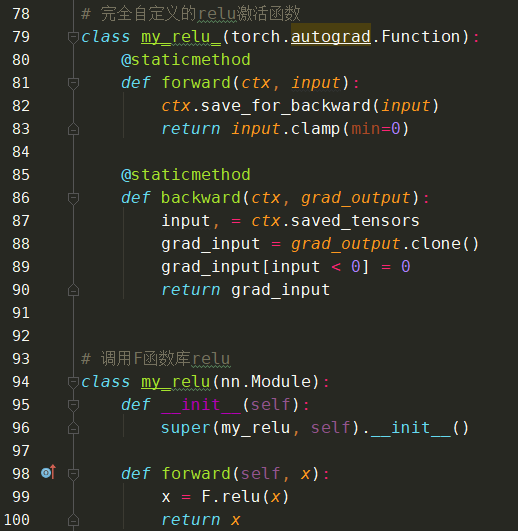
ReLU自定义如下：

 

6、死亡 ReLU：优势和缺点

    当我们将 ReLU 函数引入神经网络时，我们也引入了很大的稀疏性。那么稀疏性这个术语究竟是什么意思？

    稀疏：数量少，通常分散在很大的区域。在神经网络中，这意味着激活的矩阵含有许多 0。这种稀疏性能让我们得到什么？当某个比例（比如 50%）的激活饱和时，我们就称这个神经网络是稀疏的。这能提升时间和空间复杂度方面的效率——常数值（通常）所需空间更少，计算成本也更低。

    Yoshua Bengio 等人发现 ReLU 这种分量实际上能让神经网络表现更好，而且还有前面提到的时间和空间方面的效率。论文地址：https://www.utc.fr/~bordesan/dokuwiki/_media/en/glorot10nipsworkshop.pdf

torch.nn.ReLU(inplace=False)

torch.nn.ReLU6(inplace=False)

优点：相比于 sigmoid，由于稀疏性，时间和空间复杂度更低；不涉及成本更高的指数运算；能避免梯度消失问题。

缺点：引入了死亡 ReLU 问题，即网络的大部分分量都永远不会更新。但这有时候也是一个优势；ReLU 不能避免梯度爆炸问题。

 

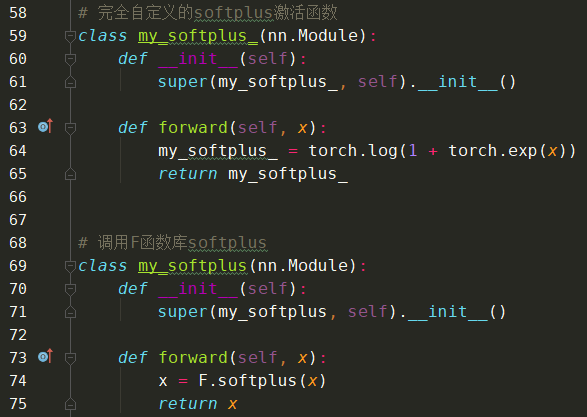
7、Softplus函数

    Softplus函数是Logistic-Sigmoid函数原函数。

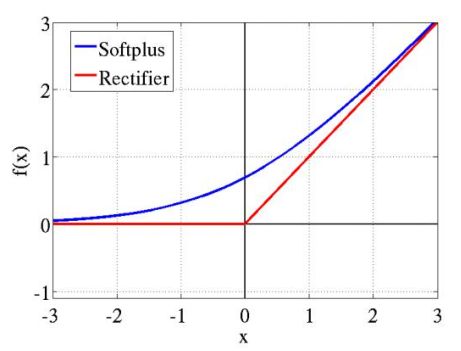
加了1是为了保证非负性。Softplus可以看作是强制非负校正函数max(0,x)平滑版本。红色的即为ReLU。

    softplus可以看作是ReLu的平滑。根据神经科学家的相关研究，softplus和ReLu与脑神经元激活频率函数有神似的地方。也就是说，相比于早期的激活函数，softplus和ReLu更加接近脑神经元的激活模型，而神经网络正是基于脑神经科学发展而来，这两个激活函数的应用促成了神经网络研究的新浪潮。

    ​Softplus自定义实现如下：

 

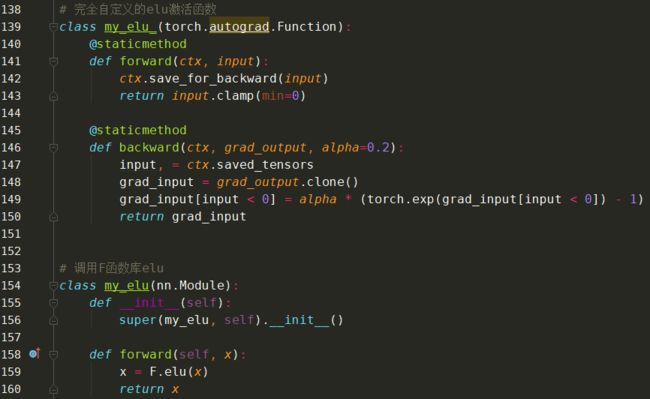
8、指数线性单元（ELU）

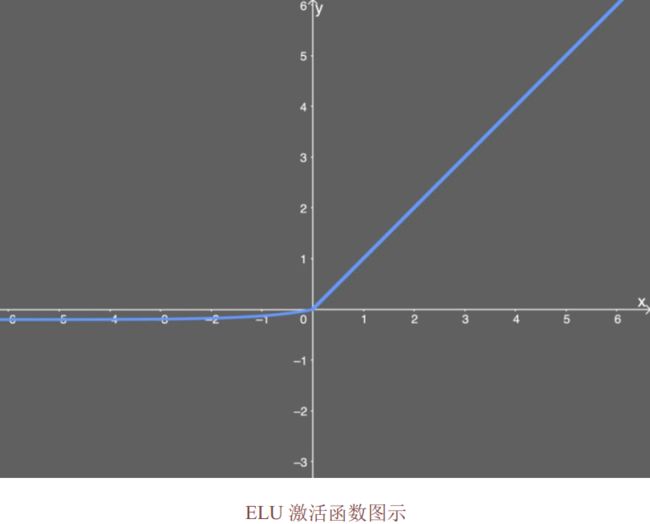
    指数线性单元激活函数解决了 ReLU 的一些问题，同时也保留了一些好的方面。这种激活函数要选取一个 α 值；常见的取值是在 0.1 到 0.3 之间。

 如果你数学不好，ELU 的公式看起来会有些难以理解：

​    ​如果你输入的 x值大于0，则结果与 ReLU 一样——即 y 值等于 x 值；但如果输入的 x 值小于 0，则我们会得到一个稍微小于 0 的值。

    ​所得到的 y 值取决于输入的 x 值，但还要兼顾参数 α——可以根据需要来调整这个参数。更进一步，我们引入了指数运算 e^x，因此 ELU 的计算成本比 ReLU 高。下面绘出了α值为 0.2 的 ELU 函数的图：

    ​上图很直观，我们应该还能很好地应对梯度消失问题，因为输入值没有映射到非常小的输出值。

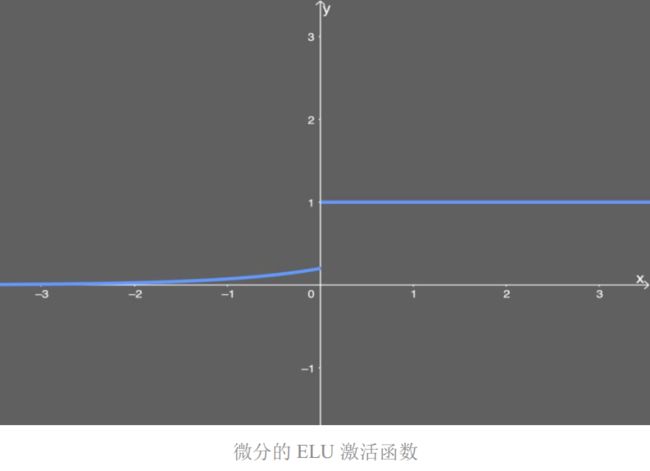
    ​但 ELU 的导数又如何呢？这同样也很重要。

    ​看起来很简单。如果输入 x 大于 0，则 y 值输出为 1；如果输入 x 小于或等于 0，则输出是 ELU 函数（未微分）加上 α 值。可绘出图为：

    你可能已经注意到，这里成功避开了死亡 ReLU 问题，同时仍保有 ReLU 激活函数的一些计算速度增益——也就是说，网络中仍还有一些死亡的分量。

torch.nn.ELU(alpha=1.0,inplace=False)

ELU自定义实现如下：

优点：能避免死亡 ReLU 问题；能得到负值输出，这能帮助网络向正确的方向推动权重和偏置变化；在计算梯度时能得到激活，而不是让它们等于 0。

缺点：由于包含指数运算，所以计算时间更长；无法避免梯度爆炸问题；神经网络不学习α值。

 

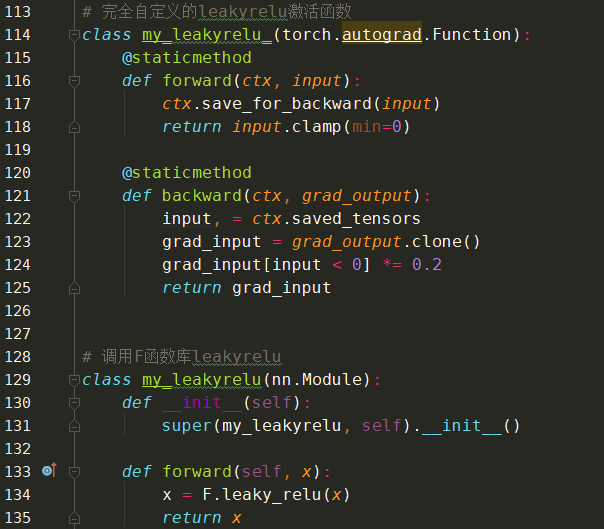
9、渗漏型整流线性单元激活函数（Leaky ReLU）

    ​渗漏型整流线性单元激活函数也有一个α值，通常取值在 0.1 到 0.3 之间。Leaky ReLU 激活函数很常用，但相比于 ELU 它也有一些缺陷，但也比 ReLU 具有一些优势。

    ​Leaky ReLU 的数学形式如下：

    ​因此，如果输入x大于 0，则输出为x；如果输入x小于或等于 0，则输出为 α 乘以输入。

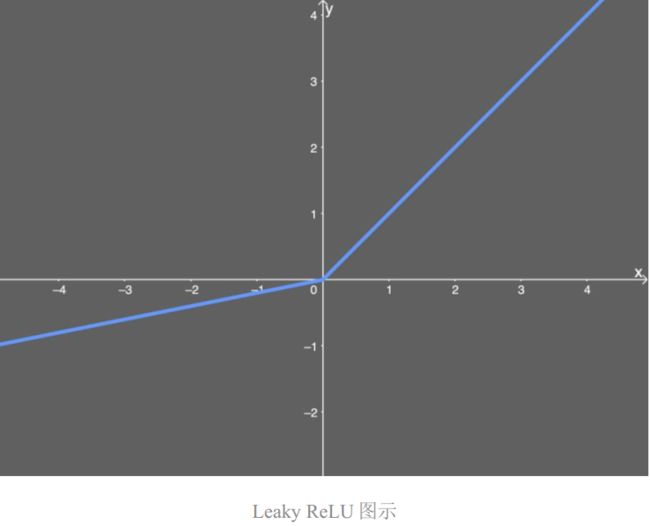
    ​这意味着能够解决死亡 ReLU 问题，因为梯度的值不再被限定为 0——另外，这个函数也能避免梯度消失问题。尽管梯度爆炸的问题依然存在，但后面的代码部分会介绍如何解决。下面给出了 Leaky ReLU 的图示，其中假设 α 值为 0.2：

    和在公式中看到的一样，如果 x 值大于 0，则任意 x 值都映射为同样的 y 值；但如果 x 值小于 0，则会多一个系数 0.2。也就是说，如果输入值 x为 -5，则映射的输出值为 -1。

    因为 Leaky ReLU 函数是两个线性部分组合起来的，所以它的导数很简单：

第一部分线性是当 x 大于 0 时，输出为 1；而当输入小于 0 时，输出就为 α 值，这里我们选择的是 0.2。

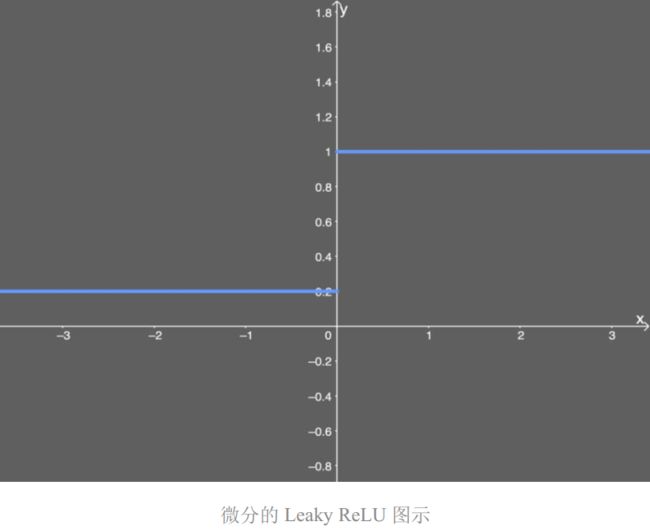
    ​从上图中也能明显地看出来，输入 x 大于或小于 0，微分的 Leaky ReLU 各为一个常量。

torch.nn.LeakyReLU(negative_slope=0.01,inplace=False)

自定义实现：

优点：类似 ELU，Leaky ReLU 也能避免死亡 ReLU 问题，因为其在计算导数时允许较小的梯度；由于不包含指数运算，所以计算速度比 ELU 快。

缺点：无法避免梯度爆炸问题；神经网络不学习 α 值；在微分时，两部分都是线性的；而 ELU 的一部分是线性的，一部分是非线性的。

 

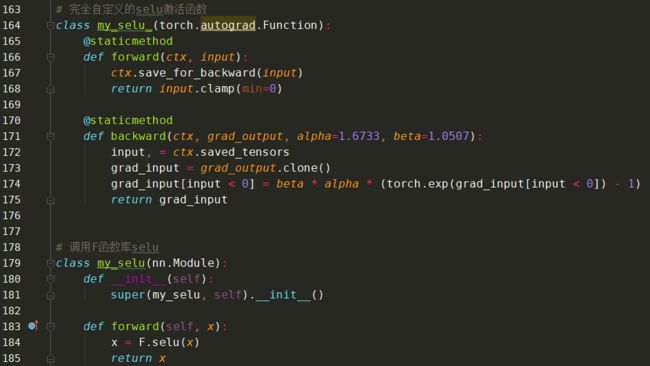
10、扩展型指数线性单元激活函数（SELU）

    ​扩展型指数线性单元激活函数比较新，介绍它的论文包含长达90页的附录（包括定理和证明等）。当实际应用这个激活函数时，必须使用 lecun_normal 进行权重初始化。如果希望应用 dropout，则应当使用 AlphaDropout。后面的代码部分会更详细地介绍。

    ​论文作者已经计算出了公式的两个值：α 和 λ；如下所示：

    ​可以看到，它们的小数点后还有很多位，这是为了绝对精度。而且它们是预先确定的，也就是说我们不必担心如何为这个激活函数选取合适的 α 值。

    ​说实话，这个公式看起来和其它公式或多或少有些类似。所有新的激活函数看起来就像是其它已有的激活函数的组合。

​    ​SELU 的公式如下：

    也就是说，如果输入值 x 大于 0，则输出值为 x 乘以 λ；如果输入值 x 小于 0，则会得到一个奇异函数——它随 x 增大而增大并趋近于 x 为 0 时的值 0.0848。本质上看，当 x 小于 0 时，先用 α 乘以 x 值的指数，再减去 α，然后乘以 λ 值。

自定义实现SELU激活函数：

 

11、SELU的特例

    SELU激活能够对神经网络进行自归一化（self-normalizing）。这是什么意思？

    ​首先，我们先看看什么是归一化（normalization）。简单来说，归一化首先是减去均值，然后除以标准差。因此，经过归一化之后，网络的组件（权重、偏置和激活）的均值为 0，标准差为 1。而这正是 SELU 激活函数的输出值。

    ​均值为 0 且标准差为 1 又如何呢？在初始化函数为 lecun_normal 的假设下，网络参数会被初始化一个正态分布（或高斯分布），然后在 SELU 的情况下，网络会在论文中描述的范围内完全地归一化。本质上看，当乘或加这样的网络分量时，网络仍被视为符合高斯分布。我们就称之为归一化。反过来，这又意味着整个网络及其最后一层的输出也是归一化的。

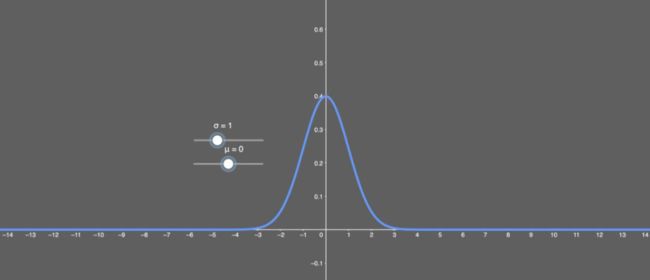
    ​均值 μ 为 0 且标准差 σ 为 1 的正态分布看起来是怎样的？

    ​SELU 的输出是归一化的，这可称为内部归一化（internal normalization），因此事实上其所有输出都是均值为 0 且标准差为 1。这不同于外部归一化（external normalization）——会用到批归一化或其它方法。

    ​很好，也就是说所有分量都会被归一化。但这是如何做到的？

    ​简单解释一下，当输入小于 0 时，方差减小；当输入大于 0 时，方差增大——而标准差是方差的平方根，这样我们就使得标准差为 1。

    ​我们通过梯度得到零均值。我们需要一些正值和负值才能让均值为 0。我的上一篇文章介绍过，梯度可以调整神经网络的权重和偏置，因此我们需要这些梯度输出一些负值和正值，这样才能控制住均值。

    ​均值 μ 和方差 ν 的主要作用是使我们有某个域 Ω，让我们总是能将均值和方差映射到预定义的区间内。这些区间定义如下：

    ∈ 符号表示均值和方差在这些预定义的区间之内。反过来，这又能避免网络出现梯度消失和爆炸问题。

    下面引述一段论文的解释，说明了他们得到这个激活函数的方式，我认为这很重要：SELU 允许构建一个映射 g，其性质能够实现 SNN（自归一化神经网络）。SNN 不能通过（扩展型）修正线性单元（ReLU）、sigmoid 单元、tanh 单元和 Leaky ReLU 实现。这个激活函数需要有：

（1）负值和正值，以便控制均值；

（2）饱和区域（导数趋近于零），以便抑制更低层中较大的方差；

（3）大于 1 的斜率，以便在更低层中的方差过小时增大方差；

（4）连续曲线。

    后者能确保一个固定点，其中方差抑制可通过方差增大来获得均衡。我们能通过乘上指数线性单元（ELU）来满足激活函数的这些性质，而且 λ>1 能够确保正值净输入的斜率大于 1。

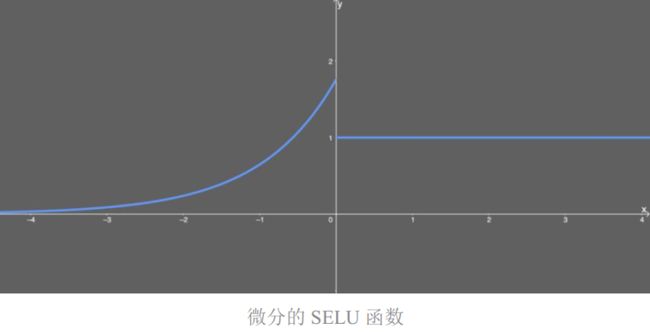
我们再看看 SELU 的微分函数：

    ​很好，不太复杂，我们可以简单地解释一下。如果 x 大于 0，则输出值为 λ；如果 x 小于 0，则输出为 α 乘以 x 的指数再乘 λ。

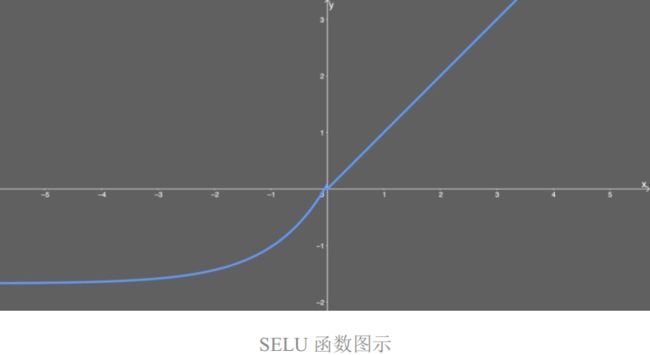
    ​其图形如下所示，看起来很特别：

    注意 SELU 函数也需要 lecun_normal 进行权重初始化；而且如果你想使用 dropout，你也必须使用名为 Alpha Dropout 的特殊版本。

自定义实现：

优点：内部归一化的速度比外部归一化快，这意味着网络能更快收敛；不可能出现梯度消失或爆炸问题，见 SELU 论文附录的定理 2 和 3。

缺点：这个激活函数相对较新——需要更多论文比较性地探索其在 CNN 和 RNN 等架构中应用。这里有一篇使用SELU 的CNN 论文：https://arxiv.org/pdf/1905.01338.pdf

 

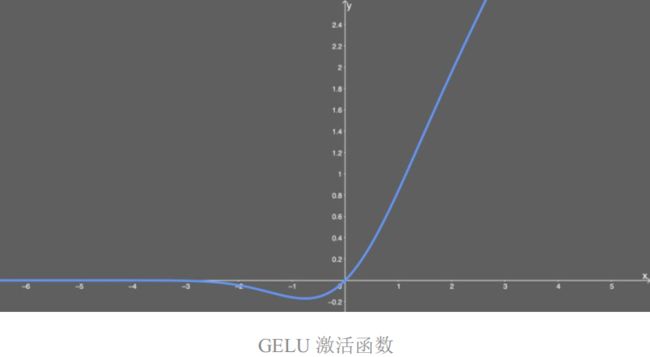
12、GELU

    高斯误差线性单元激活函数在最近的 Transformer 模型（谷歌的 BERT 和 OpenAI 的 GPT-2）中得到了应用。GELU 的论文来自 2016 年，但直到最近才引起关注。

    ​这种激活函数的形式为：

    看得出来，这就是某些函数（比如双曲正切函数 tanh）与近似数值的组合。没什么过多可说的。有意思的是这个函数的图形：

    ​可以看出，当 x 大于 0 时，输出为 x；但 x=0 到 x=1 的区间除外，这时曲线更偏向于 y 轴。

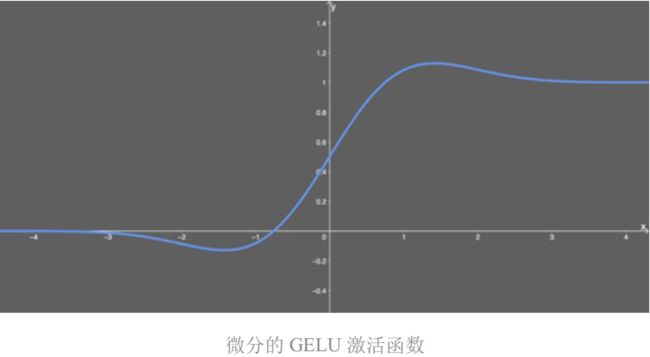
    ​我没能找到该函数的导数，所以我使用了 WolframAlpha 来微分这个函数。结果如下：

    和前面一样，这也是双曲函数的另一种组合形式。但它的图形看起来很有意思：

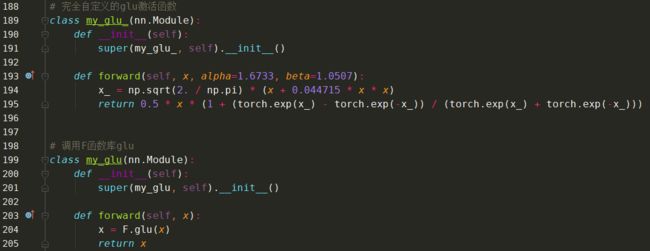
自定义实现：

优点：似乎是 NLP 领域的当前最佳；尤其在 Transformer 模型中表现最好；能避免梯度消失问题。

缺点：尽管是 2016 年提出的，但在实际应用中还是一个相当新颖的激活函数。

 

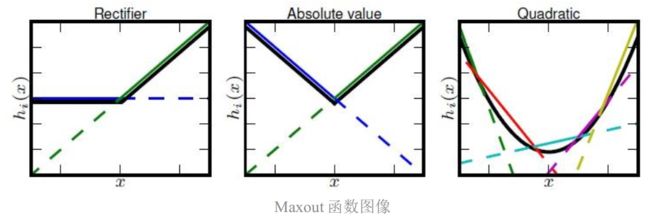
13、MaxOut激活函数

    Maxout是对ReLU和leaky ReLU的一般化归纳，函数公式是：

    Maxout非线性函数图像如下图所示。Maxout具有ReLU的优点，如计算简单，不会 saturation，同时又没有ReLU的一些缺点，如容易go die。

    存在问题：每个神经元的参数double，这就导致整体参数的数量激增。

 

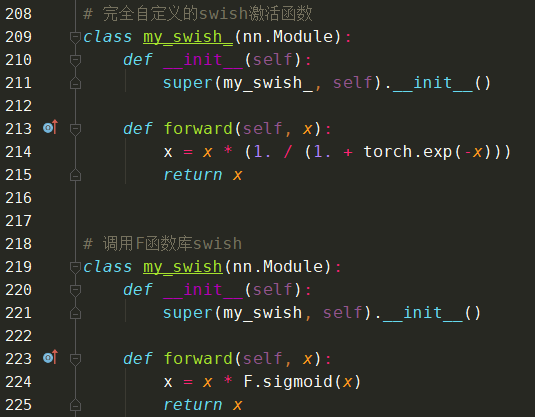
14、Swish激活函数

    Swish 的设计受到 LSTM 和 highway network 中使用 sigmoid 函数进行门控的启发。我们使用同样的值进行门控来简化门控机制，称为自门控（self-gating）。自门控的优势是它仅需要一个简单的标量输入，而正常的门控需要多个标量输入。该特性令使用自门控的激活函数如 Swish 能够轻松替换以单个标量作为输入的激活函数（如 ReLU），无需改变参数的隐藏容量或数量。

    Swish 是一种新型激活函数，公式为：

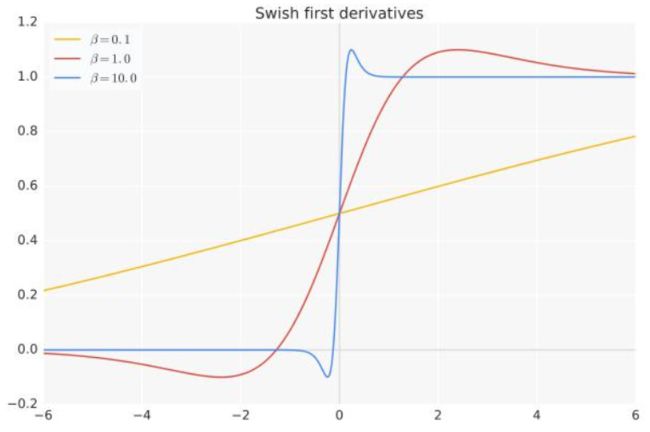
Swish （f(x) = x · sigmoid(x)）具备无上界有下界、平滑、非单调的特性。Swish激活函数图像：

Swish激活函数的导数图像：

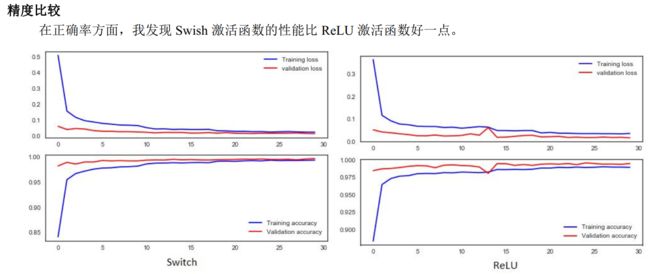
精度比较：在正确率方面，我发现 Swish 激活函数的性能比 ReLU 激活函数好一点。

Swish自定义实现：

 

15、梯度消失/爆炸原因及解决办法

原因,浅层的梯度计算需要后面各层的权重及激活函数导数的乘积,因此可能出现前层比后层的学习率小(vanishing gradient)或大(exploding)的问题,所以具有不稳定性.那么如何解决呢?

需要考虑几个方面:

1.权重初始化

2.使用合适的方式初始化权重, 如ReLU使用MSRA的初始化方式, tanh使用xavier初始化方式.

3.激活函数选择

4.激活函数要选择ReLU等梯度累乘稳定的.

5.学习率

 一种训练优化方式是对输入做白化操作(包括正规化和去相关), 目的是可以选择更大的学习率. 现代深度学习网络中常使用Batch Normalization(包括正规化步骤,但不含去相关). (All you need is a good init. If you can't find the good init, use Batch Normalization.)

    由于梯度的公式包含每层激励的导数以及权重的乘积,因此让中间层的乘积约等于1即可.但是sigmoid这种函数的导数值又与权重有关系(最大值1/4,两边对称下降),所以含有sigmoid的神经网络不容易解决,输出层的activation大部分饱和,因此不建议使用sigmoid.

    ReLU在自变量大于0时导数为1,小于0时导数为0,因此可以解决上述问题.

    梯度爆炸：由于sigmoid,ReLU等函数的梯度都在[0,1]以内，所以不会引发梯度爆炸问题。 而梯度爆炸需要采用梯度裁剪、BN、设置较小学习率等方式解决。

 

16、激活函数选择

    1.首先尝试ReLU,速度快,但要注意训练的状态.

    2.如果ReLU效果欠佳,尝试Leaky ReLU或Maxout等变种。

    3.尝试tanh正切函数(以零点为中心,零点处梯度为1)

    4.sigmoid/tanh在RNN（LSTM、注意力机制等）结构中有所应用，作为门控或者概率值.

    5.在浅层神经网络中，如不超过4层的，可选择使用多种激励函数，没有太大的影响。

    6. Sigmoid函数以及它们的联合通常在分类器的中有更好的效果 

    7. 由于梯度崩塌的问题，在某些时候需要避免使用Sigmoid和Tanh激活函数 

    8. ReLU函数是一种常见的激活函数，在目前使用是最多的 

    9. 如果遇到了一些死的神经元，我们可以使用Leaky ReLU函数 

    10. ReLU永远只在隐藏层中使用 

    11. 根据经验，一般可以从ReLU激活函数开始，但是如果ReLU不能很好的解决问题，再去尝试其他的激活函数 

    12. 如果使用 ReLU，要小心设置 learning rate，不要让网络出现很多 “dead” 神经元，如果不好解决，可以试试 Leaky ReLU、PReLU 或者 Maxout。

 

基于Fashion Minist数据集的实践对比

1、Fashion-MNIST数据集介绍

    ​Fashion-MNIST是一个替代MNIST手写数字集的图像数据集。 它是由Zalando（一家德国的时尚科技公司）旗下的研究部门提供。其涵盖了来自10种类别的共7万个不同商品的正面图片。Fashion-MNIST的大小、格式和训练集/测试集划分与原始的MNIST完全一致。60000/10000的训练测试数据划分，28x28的灰度图片。你可以直接用它来测试你的机器学习和深度学习算法性能，且不需要改动任何的代码。

这个数据集的样子大致如下（每个类别占三行）：

 

取代MNIST数据集的原因由如下几个：

    1、MNIST太简单了。 很多深度学习算法在测试集上的准确率已经达到99.6%！不妨看看我们基于scikit-learn上对经典机器学习算法的评测 和这段代码： "Most pairs of MNIST digits can be distinguished pretty well by just one pixel"

    2、MNIST被用烂了。 参考："Ian Goodfellow wants people to move away from mnist"

    3、MNIST数字识别的任务不代表现代机器学习。 参考："François Cholle: Ideas on MNIST do not transfer to real CV" 

获取数据集：

git clone [email protected]:zalandoresearch/fashion-mnist.git

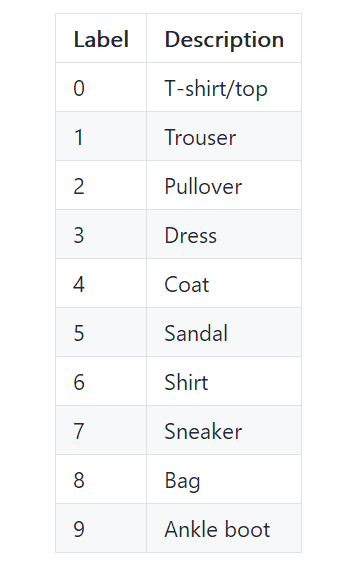
每个训练和测试样本都按照以下类别进行了标注：

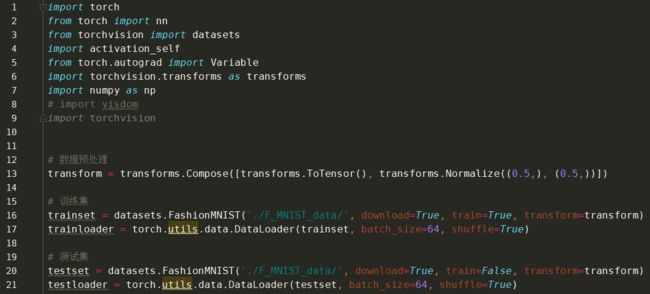
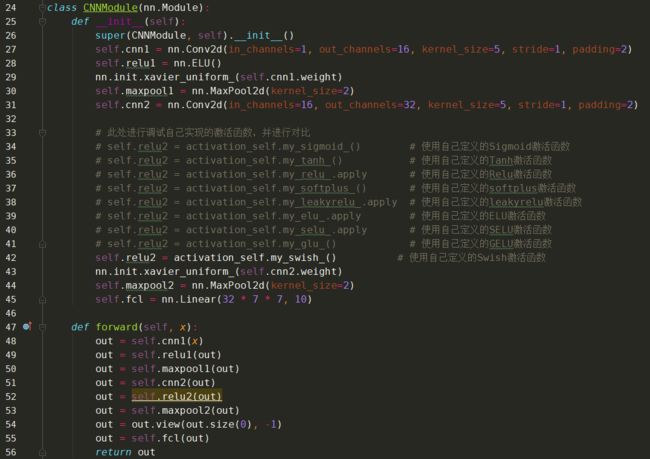
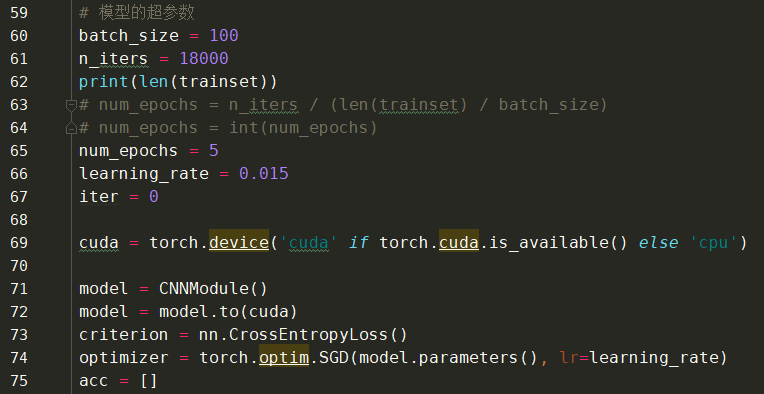
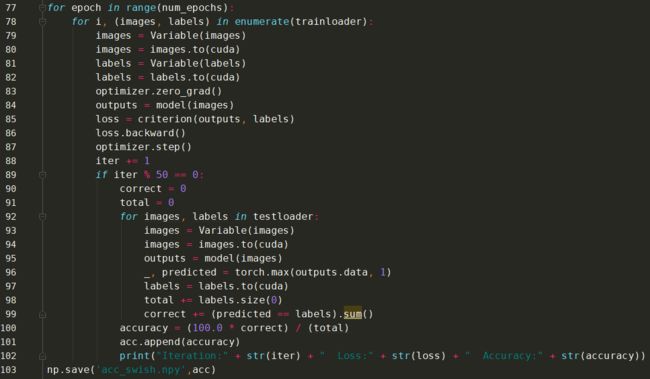
2、项目代码

 

基于不同激活函数的对比执行结果：

基于篇幅大家可以自行下载公众号的代码进行运行和对比。

关注公众号并回复【激活函数】即可获取该文章的PDF文件和项目实践代码以及自定义激活函数源码。同时，也非常期待您的打赏。

参考：

https://blog.csdn.net/clover_my/article/details/90693817

https://www.cnblogs.com/makefile/p/activation-function.html

《深度学习核心技术与实践》

声明：转载请说明出处

下方为小生公众号，还望包容接纳和关注，非常期待与您的美好相遇，让我们以梦为马，砥砺前行。

希望技术与灵魂可以一路同行

长按识别二维码关注一下更多精彩内容可回复关键词每篇文章的主题即可