说话人识别之GMM-UBM系统
GMM-UBM, 最经典代表作：
Speaker Verification Using Adapted Gaussian Mixture Models
每个人的声音都有独特的特征,这个特征由两个音素决定:
1. 声腔的尺寸
2. 发声器官被操纵的方式
这些因素使得声音变得独一无二
一：说话人识别流程
先进行特征提取,然后训练模型,最后是打分判决.
这其中特征提取包括 预加重,分帧加窗,傅里叶变换得到频谱图,
之后再进行mel滤波使频谱图更紧凑,
最后进行倒谱分析(取对数和离散余弦变换)和差分(提供一种动态特征)的到MFCC特征向量.
为了让计算机认识一个用户，我们需要将目标用户的声音提取特征，训练为一个或多个模型，存储在我们的模型库中。当我们在测试或实际使用中，实际上就是提取当前接收到的语音中的特征，将其与我们模型库中的模型进行对比判断，最终确认谁是当前语音的说话人。
二： 混合高斯模型GMM
1.UBM(Universal Background Model)
UBM其实就是一个大型的GMM模型，用来训练表示与说话人无关的特征分布。它的训练数据是某一信道下的所有人的语音数据，而不是想target模型只是反映某一个人的特征分布。说白了，只是一个大的GMM，那么训练UBM也就是训练GMM，所用算法采用的是EM算法。
GMM中，从说话人语音抽出来的D维特征矢量对应的似然率可用K个高斯分量表示： p ( x ∣ λ ) = ∑ i = 1 M w i p i ( x ) p(\boldsymbol{x} | \lambda)=\sum_{i=1}^{M} w_{i} p_{i}(\boldsymbol{x}) p(x∣λ)=i=1∑Mwipi(x)其中是第K个高斯分量的权重， ∑ i = 1 M w i = 1 \sum_{i=1}^{M} w_{i}=1 ∑i=1Mwi=1
p i ( x ) = 1 ( 2 π ) D / 2 ∣ Σ i ∣ 1 / 2 exp { − 1 2 ( x − μ i ) ′ ( Σ i ) − 1 ( x − μ i ) } p_{i}(\boldsymbol{x})=\frac{1}{(2 \pi)^{D / 2}\left|\Sigma_{i}\right|^{1 / 2}} \exp \left\{-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}_{i}\right)^{\prime}\left(\Sigma_{i}\right)^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}_{i}\right)\right\} pi(x)=(2π)D/2∣Σi∣1/21exp{−21(x−μi)′(Σi)−1(x−μi)}
整个高斯模型可以用模型参数 λ = { w i , μ i , Σ i } \lambda=\left\{w_{i}, \mu_{i}, \Sigma_{i}\right\} λ={wi,μi,Σi} i=1,2…m来表示。
2.参数调整算法 EM算法
现在的问题是如何根据已知的T个特征矢量(t=1,2,3…T)来确定GMM参数。按照极大似然估计，参数应该使这T个的平均概率最大，也就是使对数似然函数L最大。
log p ( X ∣ λ ) = ∑ t = 1 T log p ( x t ∣ λ ) \log p(X | \lambda)=\sum_{t=1}^{T} \log p\left(x_{t} | \lambda\right) logp(X∣λ)=t=1∑Tlogp(xt∣λ)
GMM参数的估计基于最大似然准则ML，通过EM迭代算法来实现，这时可以得到GMM模型中权重，均值，方差的迭代公式：
w i ′ = 1 n ∑ j n p ( i ∣ x j , θ ) μ i ′ = ∑ j n x j p ( i ∣ x j , θ ) ∑ j n p ( i ∣ x j , θ ) σ i ′ 2 = ∑ j n ( x j − μ i ′ ) 2 p ( i ∣ x j , θ ) ∑ i n p ( i ∣ x j , θ ) \begin{aligned} w_{i}^{\prime} &=\frac{1}{n} \sum_{j}^{n} p\left(i | x_{j}, \theta\right) \\ \mu_{i}^{\prime} &=\frac{\sum_{j}^{n} x_{j} p\left(i | x_{j}, \theta\right)}{\sum_{j}^{n} p\left(i | x_{j}, \theta\right)} \\ \sigma_{i}^{\prime 2} &=\frac{\sum_{j}^{n}\left(x_{j}-\mu_{i}^{\prime}\right)^{2} p\left(i | x_{j}, \theta\right)}{\sum_{i}^{n} p\left(i | x_{j}, \theta\right)} \end{aligned} wi′μi′σi′2=n1j∑np(i∣xj,θ)=∑jnp(i∣xj,θ)∑jnxjp(i∣xj,θ)=∑inp(i∣xj,θ)∑jn(xj−μi′)2p(i∣xj,θ)
其中， p ( i ∣ X j , θ ) \mathrm{p}(\mathrm{i} | \mathrm{X} j, \theta) p(i∣Xj,θ)是第i个混合分量的后验概率
p ( i ∣ x j , θ ) = w i p i ( x t ∣ θ i ) ∑ k M w k p k ( x t ∣ , θ k ) p\left(i | \mathbf{x}_{j}, \theta\right)=\frac{w_{i} p_{i}\left(\mathbf{x}_{t} | \theta_{i}\right)}{\sum_{k}^{M} w_{k} p_{k}\left(\mathbf{x}_{t} |, \theta_{k}\right)} p(i∣xj,θ)=∑kMwkpk(xt∣,θk)wipi(xt∣θi)
三、GMM-UBM
参考文章：GMM-UBM系统框架
在实际中每一个说话人的语音数据很少，这将导致无法训练出高效的GMM模型。并且由于多通道的问题，训练GMM模型的语音与测试语音存在失配的情况，这些因素都会降低声纹识别系统的性能。所以机器学习的前辈们(DA Reynolds的团队)提出了一个通用背景模型(Universal Background Model, 简称UBM)。我们可以用UBM和少量的说话人数据，通过自适应算法(如最大后验概率MAP、最大似然线性回归MLLR等，本文选择阐述MAP算法)来得到目标说话人模型。
GMM-UBM实际上是一种对GMM的改进方法，我们既然没法从目标用户那里收集到足够的语音，那就换一种思路，可以从其他地方收集到大量非目标用户的声音，我们将这些非目标用户数据（声纹识别领域称为背景数据）混合起来充分训练出一个GMM，这个GMM可以看作是对语音的表征，但是又由于它是从大量身份的混杂数据中训练而成，它又不具备表征具体身份的能力。我们可以把这种模型看作是某一个具体说话人模型的先验模型。形象的比方就是说你准备去相亲，媒人给你看了小莉的照片，你耳边浮现的肯定是小莉各种可能的温柔的声音，而不是你家旺财的叫声。这种GMM-UBM就是起到类似的作用，它对语音特征在空间分布的概率模型给出一个良好的预先估计，让我们可以提前训练GMM。然后将目标用户的数据在这个模型上进行参数的微调即可。GMM-UBM模型最重要的优势就是通过MAP算法对模型参数进行估计，避免了过拟合的发生，同时我们不必调整目标用户GMM的所有参数（权重，均值，方差）只需要对各个高斯成分的均值参数进行估计，就能实现最好的识别性能。 根据实验表明，这可以让待估的参数减少超过一半，越少的参数也意味着更快的收敛，不需要那么多的目标用户数据即可模型的良好训练。
通过上图我们可以大致的了解GMM-UBM模型的大致逻辑。用大白话讲就是，用其他用户的数据来进行“预训练”，减少对真正目标用户的训练时间和参数调整。
四、说话人模型的自适应（MAP自适应算法）
1.概述
基本思想是，从训练后的UBM模型参数通过自适应来更新其参数进而导出目标说话人的GMM模型。
- 首先，使用目标说话人的训练数据计算出UBM模型的新参数(高斯权重、均值和方差)；
- 将得到的新参数与UBM模型的原参数进行融合，从而得到目标说话人的模型。
2.MAP算法的实现
这种自适应算法分为两步：第一步，与EM算法的E-Step一样，对UBM的每个混合成分计算目标说话人训练语音的充分统计的估计；第二部与EM算法不同，这些新的充分估计与老的充分估计用一个语料相关的混合系数结合起来。具体计算方法：
- 第一步：
给定GMM模型和目标说话人的训练矢量(t=1,2,3…T)，首先算出训练矢量在UBM 混合成员中的概率分布。即对第i个混合成员：
Pr ( i ∣ x t ) = w i p i ( x t ) ∑ j = 1 M w j p j ( x t ) \operatorname{Pr}\left(i | \boldsymbol{x}_{t}\right)=\frac{w_{i} p_{i}\left(\boldsymbol{x}_{t}\right)}{\sum_{j=1}^{M} w_{j} p_{j}\left(\boldsymbol{x}_{t}\right)} Pr(i∣xt)=∑j=1Mwjpj(xt)wipi(xt)
然后利用Pr(i|)和混合加权值，平均值向量，方差进行从分统计：
n i = ∑ t = 1 T Pr ( i ∣ x t ) E i ( x ) = 1 n i ∑ t = 1 T Pr ( i ∣ x t ) x t E i ( x 2 ) = 1 n i ∑ t = 1 T Pr ( i ∣ x t ) x t 2 \begin{aligned} n_{i} &=\sum_{t=1}^{T} \operatorname{Pr}\left(i | \boldsymbol{x}_{t}\right) \\ E_{i}(\boldsymbol{x}) &=\frac{1}{n_{i}} \sum_{t=1}^{T} \operatorname{Pr}\left(i | \boldsymbol{x}_{t}\right) \boldsymbol{x}_{t} \\ E_{i}\left(\boldsymbol{x}^{2}\right) &=\frac{1}{n_{i}} \sum_{t=1}^{T} \operatorname{Pr}\left(i | \boldsymbol{x}_{t}\right) \boldsymbol{x}_{t}^{2} \end{aligned} niEi(x)Ei(x2)=t=1∑TPr(i∣xt)=ni1t=1∑TPr(i∣xt)xt=ni1t=1∑TPr(i∣xt)xt2
这里与EM算法中的E-Step一样。
最后，这些由训练数据产生的新的充分统计量用来更新UBM的第i个混合成员的充分统计量：
w ^ i = [ α i w n i / T + ( 1 − α i w ) w i ] γ μ ^ i = α i m E i ( x ) + ( 1 − α i m ) μ i σ ^ i 2 = α i v E i ( x 2 ) + ( 1 − α i v ) ( σ i 2 + μ i 2 ) − μ ^ i 2 \begin{array}{l}{\hat{w}_{i}=\left[\alpha_{i}^{w} n_{i} / T+\left(1-\alpha_{i}^{w}\right) w_{i}\right] \gamma} \\ {\hat{\boldsymbol{\mu}}_{i}=\alpha_{i}^{m} E_{i}(\boldsymbol{x})+\left(1-\alpha_{i}^{m}\right) \boldsymbol{\mu}_{i}} \\ {\hat{\boldsymbol{\sigma}}_{i}^{2}=\alpha_{i}^{v} E_{i}\left(\boldsymbol{x}^{2}\right)+\left(1-\alpha_{i}^{v}\right)\left(\boldsymbol{\sigma}_{i}^{2}+\boldsymbol{\mu}_{i}^{2}\right)-\hat{\boldsymbol{\mu}}_{i}^{2}}\end{array} w^i=[αiwni/T+(1−αiw)wi]γμ^i=αimEi(x)+(1−αim)μiσ^i2=αivEi(x2)+(1−αiv)(σi2+μi2)−μ^i2
其中， { α i w , α i m , α i v } \left\{\alpha_{i}^{w}, \alpha_{i}^{m}, \alpha_{i}^{v}\right\} {αiw,αim,αiv}是自适应系数，用来控制新的和老的估计量之间的平衡，分别控制权重，均值，方差。
自适应系数定义为 α i ρ = n i n i + r ρ , ρ ∈ { w , m , v } \alpha_{i}^{\rho}=\frac{n_{i}}{n_{i}+r^{\rho}}, \quad \rho \in\{w, m, v\} αiρ=ni+rρni,ρ∈{w,m,v}
r ρ r^{\rho} rρ是一个固定参数的因子。通常，只有平均均值向量做自适应的时候会得到最好的识别率，因此，我们只对话着模型中每个高斯分布的平均值向量做自适应。
- 第二步：测试：对数似然比（LLR）
测试特征矢量序列X的对数似然比可用下式来计算：
Λ ( X ) = log p ( X ∣ λ h y p ) − log p ( X ∣ λ u b m ) \Lambda(X)=\log p\left(X | \lambda_{\mathrm{hyp}}\right)-\log p\left(X | \lambda_{\mathrm{ubm}}\right) Λ(X)=logp(X∣λhyp)−logp(X∣λubm)
因为目标说话人模型是从UBM 模型自适应得来的，所以，对数似然比可以用快速的方法来计算。该方法基于两个事实，第一，当一个大型的GMM对一个特征矢量进行测评时，只有少数的混合成员对最终的似然值有贡献。这样似然值可以用前C个最佳混合成员的得分来近似；第二个方面是自适应后的GMM仍然保留了与UBM 相对应的混合成员。在实际计算中C通常取5或10 。
五、性能影响
1.类型不同的影响
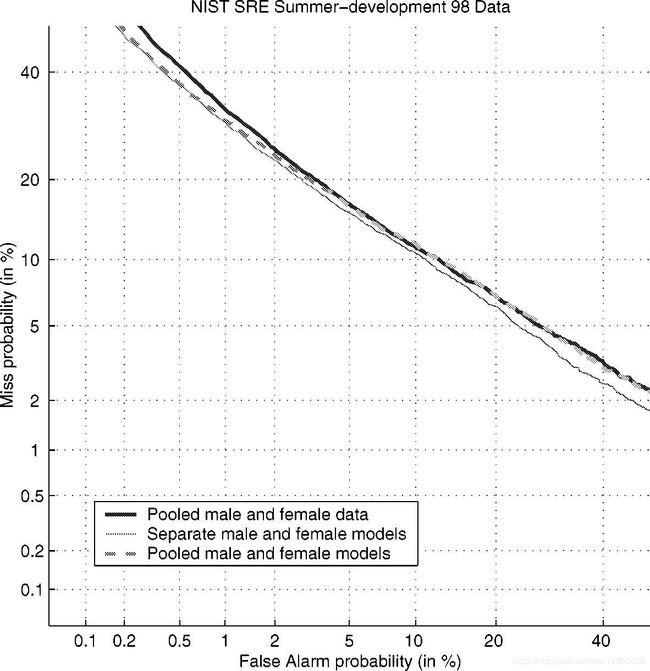三种UBM组合物的DET曲线：汇集的男性和女性数据，单独的男性和女性模型，以及合并的男性和女性模型。
虽然差异不大，但单独的男性和女性UBM表现略好于性别独立模型。
2.模型大小的影响
同样，HNORM未应用。 不同模型阶的DET曲线如图所示。从这些DET中，似乎性能曲线中的拐点大约为512个混合物。
3.参数调整的影响
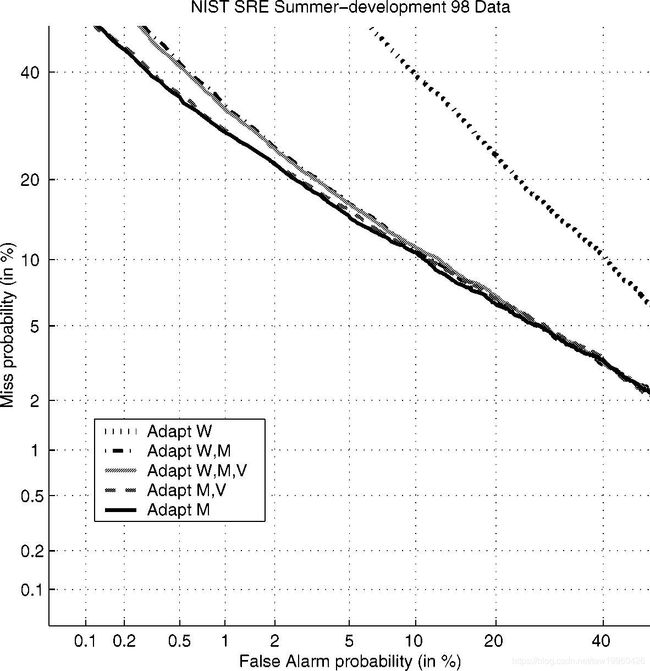
W =权重，M =均值，V =方差。我们显示了参数调整的所有组合的DET曲线。 曲线表明，调整权重会降低性能。 目前尚不清楚为什么调整权重会降低性能。 最佳的整体性能来自于仅适应平均向量
4.HNORM的影响
归一化对数似然得分（HNORM）
Λ H N O R M ( X ) = Λ ( X ) − μ ( H S ( X ) ) σ ( H S ( X ) ) \Lambda^{\mathrm{HNORM}}(X)=\frac{\Lambda(X)-\mu(H S(X))}{\sigma(H S(X))} ΛHNORM(X)=σ(HS(X))Λ(X)−μ(HS(X))
H S ( X ) H S(X) HS(X)是标签
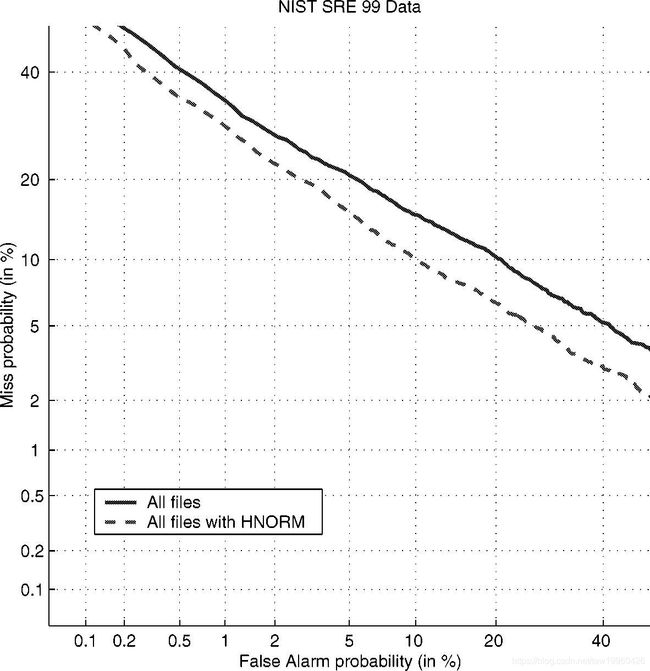
SNST =相同数字，相同类型，DNST =不同数字，相同类型，DNDT =不同数量，不同类型。
HNORM在所有操作点上都比基线系统提供了显着的性能提升
六、matlab实现
直接运行demo_gmm_ubm_artificial
参考代码链接：链接：https://pan.baidu.com/s/1cKaRCLCgnoa4pGjN3hHCEQ
提取码：feiw
