相较于完全贪心的单点爬山算法,模拟退火用概率接受新解的方式,对贪心法容易陷入局部最优解的缺陷进行了改进,是一种常用的在大的搜索空间中逼近全局最优解的元启发式方法。这里先大致描述算法。然后先用一个简单的求函数最小值例子,解释我写的c++模拟退火算法模板的基本使用,之后用其解决15节点的TSP问题,并与动态规划得到的全局最优解进行比较,解释模拟退火算法解决一般问题的方法和效果。
算法描述:
随机从一个合法解s开始,从s扩展出足够的状态,对于新的状态,若新状态优于原始状态,则接受新解,否则,以一定的概率接受新解(这保证了算法有机会跳出局部最优解),而该概率随算法运行时间下降,类似于粒子退火的过程(这也是合理的,因为随着算法的进行,当前解就逐步逼近于最优解,那么接受新解的概率自然要下降)。
其实模拟退火就是不停的基于当前最优解,试图进行改良,并且以概率接受不是那么好的解来避免陷入局部最优解,并不复杂。
算法伪代码:

模拟退火模板题: 求函数(x - 2)*(x + 3)*(x + 8)*(x - 9)的最小值
分析:
直接使用模板即可。在定义问题时,关键要素有如下几个:
1. 状态的定义
2. 对应于一个状态的效用值的计算
3. 产生新解的方式
然后还要注意的是,参数的调整,比如时间到温度如何转化,迭代次数等等。参数调整也是所有这些非经典算法都要考虑的问题。
代码:
#include
#include
#include
最后结果可以大致稳定在x=6.5左右,某次运行结果为x=6.492 y=-1549.72.
在求解过程中,当前解的演变过程如下:
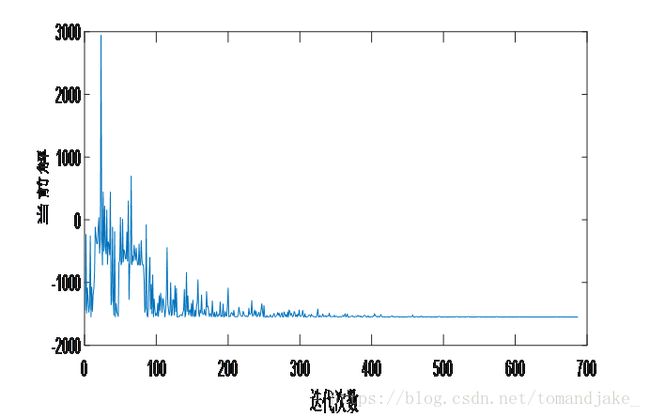
可以看到随着迭代的次数增加,当前解逐步趋向于最小值,过程类似于粒子退火,初始时能量大,无序性大,最后趋于稳定。
该函数的图形如下:
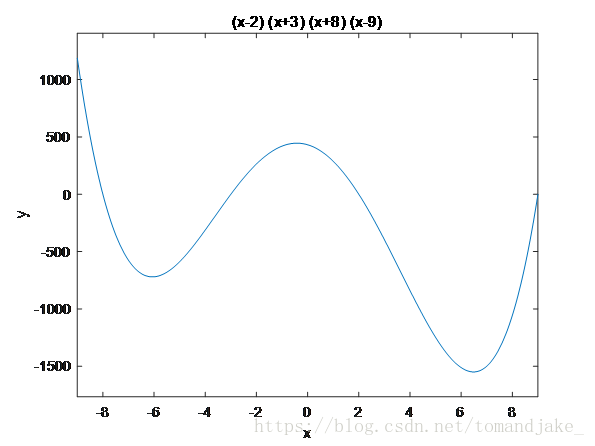
可以看出得出的结果接近于全局最优值。
15节点的TSP问题:
问题描述:
有15个城市, 给出每个城市的坐标,每两个城市之间相互有路径可走,需要消耗一定的费用。问一个商人,想从某个起点出发经过每个城市一次且仅仅一次最后回到起点所需的最小费用是多少。本题直接把两点的距离作为费用。
数据:
53.7121 15.3046 51.1758 0.0322 46.3253 28.2753 30.3313 6.9348
56.5432 21.4188 10.8198 16.2529 22.7891 23.1045 10.1584 12.4819
20.1050 15.4562 1.9451 0.2057 26.4951 22.1221 31.4847 8.9640
26.2418 18.1760 44.0356 13.5401 28.9836 25.9879
从上到下,从左往右,每两个数代表一个城市的x 和y 坐标。
分析:
仍然使用模拟退火算法。同样需要考虑三个问题:状态的定义,效用值得计算,产生新解的方式。 具体看代码。
代码:
#include
#include
#include
#include
#include
#include
#include
#include
结果能稳定在170上下,某次运行结果如下:
161.241317 (最小总费用)
2 14 10 6 12 8 5 7 9 3 11 13 1 0 4 (路径,城市下标从0开始)
解的演变过程如下:
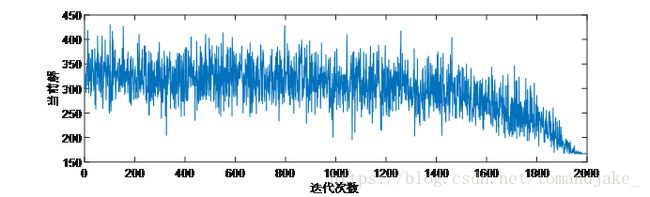
动态规划验证:
由于这里的重点只在模拟退火算法,这里只给出动态规划的状态转移方程,不做更多的解释了。
dp(S,i) 表示当前处在城市i上,已经走过bitset集合S中的城市,所耗费的最小费用。
所以状态转移方程如下:
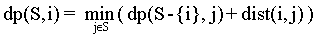
其中 dist(i,j) 表示城市i和j之间的距离(或是说费用),初始条件dp(1,0)=0,时间复杂度大致为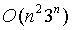
代码:
#include
#include
#include
#include
#include
#include
#include
#include
所得结果如下:
161.241
1 13 11 3 9 7 5 8 12 6 10 14 2 4 0
与以上模拟退火算法结果一致。
现在将maxn调至50,模拟退火算法很快给出结果:
300.458339
4 37 33 2 30 27 43 0 23 48 1 32 31 13 11 17 3 35 36 8 25 12 34 28 15 45 18 16 14 10 6 40 41 21 44 38 47 5 22 7 49 24 46 9 29 42 39 26 19 20
而因动态规划的时空复杂度过高,此时动态规划无法求解。
结论:
模拟退火算法能有效求解一般优化问题,并且能通过调整参数在较短的时间内得到很好的结果。是一个在找不到多项式复杂度算法的情况下求解一般较大规模优化问题的较好选择。
![]()



