组合数学作业整理与解题思路总结:容斥原理, 生成函数和递归函数
组合数学作业整理与解题思路总结:
容斥原理, 生成函数和递归函数
-
容斥原理部分:
要明确, 对组合计数问题应用容斥原理的一般方法: 找到问题所关注的, 所需要拥有的性质的反面, 求出全体计数的个数和所有不满足这些性质的计数个数, 并且将两者相减, 得到的才是我们所需要的计数数量. 对性质的把握和判断切勿出错.
以"应用容斥原理求满足某些性质的整数多元方程解或整数多元不等式解"问题为例:
- “ x ⩽ b x\leqslant b x⩽b” 的反面是 x ⩾ b + 1 x \geqslant b+1 x⩾b+1, 而非 x ⩾ b x\geqslant b x⩾b.
- 由第一章所介绍的内容我们知道: 当我们使用隔板模型解决分划问题时, 对 n n n 个可选项而言, 实际可插入隔板的位置只有 n − 1 n-1 n−1 个, 将一群物体分为 k k k 份也只需要插入 k − 1 k-1 k−1 块隔板, 因此在遇到相关问题构造组合数时切记要减掉 1 1 1.
- 对于隔板分划问题, 在不对隔板和被划分物进行一些技巧性操作的前提下, 我们得到的每一个划分中都至少有一个物体. 要让所得划分中至少有 0 0 0 个物体, 就需要相应地 加上 可选项. 反之, 则需要 减去 可选项.
-
生成函数部分:
我们的一般目标是将组合计数问题化为对某一个级数的特定幂次所对应项的系数计算问题. 因此, 若要真正解决这个问题, 就不能仅仅求出某问题生成函数的closed form, 因为这是不能直接解决问题, 必须要将它展开为和 x x x 有关的级数, 这样才能得到相应系数的计算公式.-
在生成函数
closed form的计算和简化中, 常用到下列式子:i. 1 1 − x = ∑ i = 0 ∞ x i \frac{1}{1-x} = \sum_{i = 0}^{\infty}x^{i} 1−x1=∑i=0∞xi
ii. 1 + x ( 1 − x ) 3 = ∑ n = 0 ∞ ( n + 1 ) 2 x n . \frac{1+x}{(1-x)^3} = \sum_{n = 0}^{\infty}(n+1)^2x^n. (1−x)31+x=∑n=0∞(n+1)2xn.
iii. 1 ( 1 − x ) 2 = ∑ n = 0 ∞ ( n + 1 ) x n \frac{1}{(1-x)^2} = \sum_{n = 0}^{\infty}(n+1)x^n (1−x)21=∑n=0∞(n+1)xn
iv. 2 ( 1 − x ) 3 = ∑ n = 0 ∞ ( n + 2 ) ( n + 1 ) x n \frac{2}{(1-x)^3} = \sum_{n = 0}^{\infty}(n+2)(n+1)x^{n} (1−x)32=∑n=0∞(n+2)(n+1)xn -
在使用生成函数解决多元整数不等式满足约束条件的解的组数问题时, 通常会发现使用常规思维方式无法构造有效约束不等式条件的生成函数. 第 9 9 9 题就是这样的一个例子. 事实上, 如果将整个不等式化为 f ( x ) ⩾ 0 f(x)\geqslant 0 f(x)⩾0 的形式, 我们会立即发现 f ( x ) f(x) f(x) 恰好就是一个大于等于 0 0 0 的整数, 可以对它直接套用生成函数 1 + x + x 2 + ⋯ 1+x+x^2+\cdots 1+x+x2+⋯.
-
-
递归函数部分:
- 一般情况下我们会使用特征多项式法求解形为多元齐次线性方程的递归函数. 对它的求解方式和存在重根情形的处理方式极其类似于求解高阶齐次线性常微分方程的情形, 在此不再赘述.
- 需要注意的是, 在某些情况下, 我们求解得到的一般式不完全满足所有的初值条件. 在这种情况下, 为了保证一般式可以正常 “启动” 并能递推到无穷项, 我们需要 “捏造” 几个关键的初值条件.
- 若递归函数的非齐次部分不为 0 0 0, 我们需要求出非齐次部分的特解, 将其与齐次部分的通解相加, 才可得递归函数的通解. 一般地, 我们可以将非齐次部分 f ( n ) f(n) f(n) 表示为一个幂函数和一个多项式相乘的形式:
f ( n ) = t 0 n ( A 0 + A 1 n + ⋯ + A r n r ) f(n) = t_{0}^n(A_0 + A_1n + \cdots + A_rn^r) f(n)=t0n(A0+A1n+⋯+Arnr) 则可设非齐次部分特解 H ∗ ( n ) = t n ⋅ n m ( P 0 + ⋯ + P r n r ) H^{*}(n) = t^n\cdot n^m(P_0 + \cdots + P_{r}n^r) H∗(n)=tn⋅nm(P0+⋯+Prnr), m m m 为假设 t 0 t_0 t0 为特征多项式的根, 其对应的重数, 若它不为根, 重数为 0 0 0. - 一般我们使用更为简便的特征根法求解递归函数, 但有的时候我们也不得不使用生成函数求解递归函数. 以 17 17 17 题为例, 若需要求解这样的, 非齐次部分为一个幂函数的生成函数, 我们可以首先在等式两端同乘 x n x^n xn 并对 n n n 求和, 这样可以将幂函数转化为方便操作的几何级数.
1. How many positive integers less than or equal to 100 are divisible by 2? How many positive integers less than or equal to 100 are divisible by 5? Use this information to determine how many positive integers less than or equal to 100 are divisible by neither 2 nor 5.
[Solution]
By the knowledge of Number Theory:
there are 50 50 50 positive integers which is divisible by 2;
there are 20 20 20 positive integers which is divisible by 5.
Define Property P 1 , P 2 P_1,P_2 P1,P2 as:
P 1 P_1 P1: the number is not divisible by 2.
P 2 P_2 P2: the number is not divisible by 5.
From Inclusion-Exclusion Principle, we know that the number of integers which meet neither of these two properties is:
100 − ∣ P 1 ∣ − ∣ P 2 ∣ + ∣ P 1 ∩ P 2 ∣ = 100 − 50 − 20 + 10 = 40. 100 - |P_1| - |P_2| + |P_{1}\cap P_{2}| = 100-50-20+10 = 40. 100−∣P1∣−∣P2∣+∣P1∩P2∣=100−50−20+10=40.
2. How many positive integers less than or equal to 100 are divisible by none of 2, 3, and 5?
[Solution]
By the knowledge of Number Theory:
there are 50 50 50 positive integers which is divisible by 2;
there are 33 33 33 positive integers which is divisible by 3;
there are 20 20 20 positive integers which is divisible by 5.
Define Property P 1 , P 2 P_1,P_2 P1,P2 as:
P 1 P_1 P1: the number is not divisible by 2.
P 2 P_2 P2: the number is not divisible by 3.
P 3 P_3 P3: the number is not divisible by 5.
From Inclusion-Exclusion Principle, we know that the number of integers which meet neither of these two properties is:
100 − ( ∣ P 1 ∣ + ∣ P 2 ∣ + ∣ P 3 ) + ( ∣ P 1 , 2 ∣ + ∣ P 1 , 3 ∣ + ∣ P 2 , 3 ∣ ) − ∣ P 1 , 2 , 3 ∣ = 100 − 103 + 32 − 3 = 26. 100 - (|P_1| + |P_2| + |P_3) + (|P_{1,2}| + |P_{1,3}| + |P_{2,3}|) - |P_{1,2,3}| \\ = 100-103 + 32 -3 = 26. 100−(∣P1∣+∣P2∣+∣P3)+(∣P1,2∣+∣P1,3∣+∣P2,3∣)−∣P1,2,3∣=100−103+32−3=26.
3. 求等式
∑ i = 1 5 x i = 60 \sum_{i=1}^{5}x_i = 60 i=1∑5xi=60
满足条件
x 1 ⩾ 1 , 2 ⩽ x 2 ⩽ 7 , 0 ⩽ x 3 ⩽ 6 , 3 ⩽ x 4 ⩽ 8 , x 5 ⩾ 5 x_1\geqslant 1, 2\leqslant x_2\leqslant 7, 0\leqslant x_3\leqslant 6, 3\leqslant x_4 \leqslant 8, x_5\geqslant 5 x1⩾1,2⩽x2⩽7,0⩽x3⩽6,3⩽x4⩽8,x5⩾5
的整数解组数.
[解]
记
P : x 1 ⩾ 1 , x 2 ⩾ 2 , x 3 ⩾ 0 , x 4 ⩾ 3 , x 5 ⩾ 5. P 1 : x 2 ⩾ 8. P: x_1\geqslant 1, x_2\geqslant 2, x_3\geqslant 0,x_4\geqslant 3, x_5\geqslant5. ~~~~~~ P_1: x_2\geqslant 8. P:x1⩾1,x2⩾2,x3⩾0,x4⩾3,x5⩾5. P1:x2⩾8.
P 2 : x 3 ⩾ 7. P 3 : x 4 ⩾ 9. P_2: x_3\geqslant 7. ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~P_3: x_4\geqslant 9. P2:x3⩾7. P3:x4⩾9.
. . . . . . ...... ......
并记 X 1 X_1 X1 为满足题目条件的整数解所组成的集合.
知如下结论:
∣ P ∣ = ( 53 4 ) , ∣ P 1 ∣ = ( 47 4 ) , ∣ P 2 ∣ = ( 47 4 ) , ∣ P 3 ∣ = ( 46 4 ) , ∣ P 1 , 2 ∣ = ( 40 4 ) , ∣ P 1 , 3 ∣ = ( 41 4 ) , ∣ P 2 , 3 ∣ = ( 40 4 ) , ∣ P 1 , 2 , 3 ∣ = ( 34 4 ) . |P| = \binom{53}{4},~~ |P_1| = \binom{47}{4}, ~~ |P_2| = \binom{47}{4}, ~~ |P_3| = \binom{46}{4}, \\ |P_{1,2}| = \binom{40}{4}, ~~ |P_{1,3}| = \binom{41}{4}, ~~ |P_{2,3}| = \binom{40}{4}, ~~ |P_{1,2,3}| = \binom{34}{4}. ∣P∣=(453), ∣P1∣=(447), ∣P2∣=(447), ∣P3∣=(446),∣P1,2∣=(440), ∣P1,3∣=(441), ∣P2,3∣=(440), ∣P1,2,3∣=(434).
由容斥原理:
∣ X 1 ∣ = ∣ P ∣ − ( ∣ P 1 ∣ + ∣ P 2 ∣ + ∣ P 3 ∣ ) + ( P 1 , 2 + P 1 , 3 + P 2 , 3 ) − P 1 , 2 , 3 = ( 53 4 ) − ( ( 47 4 ) + ( 47 4 ) + ( 46 4 ) ) + ( ( 40 4 ) + ( 41 4 ) + ( 40 4 ) ) − ( 34 4 ) . |X_1| = |P| - (|P_1| + |P_2| + |P_3|) + (P_{1,2} + P_{1,3} + P_{2,3}) - P_{1,2,3} \\ =\binom{53}{4} - (\binom{47}{4} + \binom{47}{4} + \binom{46}{4}) + (\binom{40}{4} + \binom{41}{4} + \binom{40}{4}) - \binom{34}{4}. ∣X1∣=∣P∣−(∣P1∣+∣P2∣+∣P3∣)+(P1,2+P1,3+P2,3)−P1,2,3=(453)−((447)+(447)+(446))+((440)+(441)+(440))−(434).
4. How many integer solutions are there to the equation
x 1 + x 2 + x 3 + x 4 = 32 x_1 + x_2 + x_3 + x_4 = 32 x1+x2+x3+x4=32
with
0 ≤ x i ≤ 10 0 ≤ x_i ≤ 10 0≤xi≤10
for
i = 1 , 2 , 3 , 4 ? i = 1, 2, 3, 4? i=1,2,3,4?
[Solution]
Assume Property P i P_i Pi stands for number i i i is greater than 11 11 11. Immediately we have:
∣ P 1 ∣ = ∣ P 2 ∣ = ∣ P 3 ∣ = ∣ P 4 ∣ = ( 24 3 ) . |P_1| = |P_2| = |P_3| = |P_4| = \binom{24}{3}. ∣P1∣=∣P2∣=∣P3∣=∣P4∣=(324).
∣ P 1 , 2 ∣ = ∣ P 1 , 3 ∣ = ∣ P 1 , 4 ∣ = ∣ P 2 , 3 ∣ = ∣ P 2 , 4 ∣ = ∣ P 3 , 4 ∣ = ( 13 3 ) . |P_{1,2}| = |P_{1,3}| = |P_{1,4}| = |P_{2,3}| = |P_{2,4}| = |P_{3,4}| = \binom{13}{3}. ∣P1,2∣=∣P1,3∣=∣P1,4∣=∣P2,3∣=∣P2,4∣=∣P3,4∣=(313).
∣ P 1 , 2 , 3 ∣ = ∣ P 1 , 2 , 4 ∣ = ∣ P 2 , 3 , 4 ∣ = ∣ P 1 , 2 , 3 , 4 ∣ = 0 |P_{1,2,3}| = |P_{1,2,4}| = |P_{2,3,4}| = |P_{1,2,3,4}| = 0 ∣P1,2,3∣=∣P1,2,4∣=∣P2,3,4∣=∣P1,2,3,4∣=0.
From the Inclusion-Exclusion Principle: we know that the solution which does not meet property 1 , 2 , 3 , 4 1,2,3,4 1,2,3,4 is:
( 35 3 ) − 4 ⋅ ( 24 3 ) + 6 ⋅ ( 13 3 ) − 3 ⋅ 0 + 0. \binom{35}{3} - 4\cdot \binom{24}{3} + 6\cdot \binom{13}{3} - 3\cdot 0 + 0. (335)−4⋅(324)+6⋅(313)−3⋅0+0.
5. How many integer solutions are there to the inequality
y 1 + y 2 + y 3 + y 4 < 184 y_1 + y_2 + y_3 + y_4 < 184 y1+y2+y3+y4<184
with
y 1 > 0 , 0 < y 2 ≤ 10 , 0 ≤ y 3 ≤ 17 y_1 > 0, 0 < y_2 ≤ 10, 0 ≤ y_3 ≤ 17 y1>0,0<y2≤10,0≤y3≤17
and
0 ≤ y 4 < 19 ? 0 ≤ y_4 < 19? 0≤y4<19?
[Solution]
Assume P i , i ∈ [ 3 ] P_i, i\in [3] Pi,i∈[3] stands for y 2 ⩾ 11 , y 3 ⩾ 18 , y 4 ⩾ 20 y_2 \geqslant 11, ~ ~ y_3 \geqslant 18,~~ y_4\geqslant 20 y2⩾11, y3⩾18, y4⩾20.
Also, we stipulate that ( i j ) = 0 \binom{i}{j} = 0 (ji)=0, if i < j i
for every i i i in [ 184 − 1 ] [184-1] [184−1]:
∣ P 1 ∣ = ( i − 9 3 ) ∣ P 2 ∣ = ( i − 17 3 ) |P_{1}| = \binom{i-9}{3} ~~~~~|P_{2}| = \binom{i-17}{3} ∣P1∣=(3i−9) ∣P2∣=(3i−17)
∣ P 2 ∣ = ( i − 17 3 ) ∣ P 3 ∣ = ( i − 18 3 ) |P_{2}| = \binom{i-17}{3} ~~ ~~|P_{3}| = \binom{i-18}{3} ∣P2∣=(3i−17) ∣P3∣=(3i−18)
∣ P 1 , 2 ∣ = ( i − 28 3 ) ∣ P 1 , 3 ∣ = ( i − 29 3 ) |P_{1,2}| = \binom{i-28}{3} ~~ |P_{1,3}| = \binom{i-29}{3} ∣P1,2∣=(3i−28) ∣P1,3∣=(3i−29)
∣ P 2 , 3 ∣ = ( i − 36 3 ) ∣ P 1 , 2 , 3 ∣ = ( i − 46 3 ) |P_{2,3}| = \binom{i-36}{3} ~~ |P_{1,2,3}| = \binom{i-46}{3} ∣P2,3∣=(3i−36) ∣P1,2,3∣=(3i−46)
Immediately, we know that for every i i i in [ 183 ] [183] [183]:
The number of integer solutions which meet the requirement is
( i + 1 3 ) − ( ( i − 9 3 ) + ( i − 17 3 ) + ( i − 18 3 ) ) + ( ( i − 28 3 ) + ( i − 29 3 ) + ( i − 36 3 ) ) − ( i − 46 3 ) . \binom{i+1}{3} - (\binom{i-9}{3} + \binom{i-17}{3} + \binom{i-18}{3}) + (\binom{i-28}{3} + \binom{i-29}{3} + \binom{i-36}{3}) - \binom{i-46}{3}. (3i+1)−((3i−9)+(3i−17)+(3i−18))+((3i−28)+(3i−29)+(3i−36))−(3i−46).
So, the total number of required integer solution is:
∑ i = 2 183 { ( i + 1 3 ) − ( ( i − 9 3 ) + ( i − 17 3 ) + ( i − 18 3 ) ) + ( ( i − 28 3 ) + ( i − 29 3 ) + ( i − 36 3 ) ) − ( i − 46 3 ) } . \sum_{i=2}^{183}\{\binom{i+1}{3} - (\binom{i-9}{3} + \binom{i-17}{3} + \binom{i-18}{3}) + (\binom{i-28}{3} + \binom{i-29}{3} + \binom{i-36}{3}) - \binom{i-46}{3}\}. i=2∑183{(3i+1)−((3i−9)+(3i−17)+(3i−18))+((3i−28)+(3i−29)+(3i−36))−(3i−46)}.
6. Find the closed form of the generating functions of:
1. { ( n + 1 ) 3 } n = 0 ∞ \{(n+1)^3\}_{n = 0}^{\infty} {(n+1)3}n=0∞
[Solution]
Define
f ( x ) = ∑ n = 0 ∞ ( n + 1 ) 2 x n . f(x) = \sum_{n = 0}^{\infty}(n+1)^2x^n. f(x)=n=0∑∞(n+1)2xn.
From the solution above, we have:
1 + x ( 1 − x ) 3 = ∑ n = 0 ∞ ( n + 1 ) 2 x n . \frac{1+x}{(1-x)^3} = \sum_{n = 0}^{\infty}(n+1)^2x^n. (1−x)31+x=n=0∑∞(n+1)2xn.
also
∑ i = 0 ∞ ( n + 1 ) 2 x n + 1 = x 2 + x ( 1 − x ) 3 \sum_{i = 0}^{\infty}(n+1)^2x^{n+1} = \frac{x^2 + x}{(1-x)^3} i=0∑∞(n+1)2xn+1=(1−x)3x2+x
d d x x 2 + x ( 1 − x ) 3 = ∑ n = 0 ∞ ( n + 1 ) 3 x n . \frac{d}{dx}\frac{x^2 + x}{(1-x)^3} = \sum_{n = 0}^{\infty}(n+1)^3x^n. dxd(1−x)3x2+x=n=0∑∞(n+1)3xn.
since
d d x x 2 + x ( 1 − x ) 3 = x 2 + 4 x + 1 ( 1 − x ) 4 \frac{d}{dx}\frac{x^2 + x}{(1-x)^3} = \frac{x^2 + 4x + 1}{(1-x)^4} dxd(1−x)3x2+x=(1−x)4x2+4x+1
The closed form of its generated function is:
x 2 + 4 x + 1 ( 1 − x ) 4 . \frac{x^2 + 4x + 1}{(1-x)^4}. (1−x)4x2+4x+1.
2. { ( n + 1 ) ( n + 2 ) 2 } n = 0 ∞ \{\frac{(n+1)(n+2)}{2}\}_{n = 0}^{\infty} {2(n+1)(n+2)}n=0∞
[Solution]
Define
f ( x ) = ∑ n = 0 ∞ ( n + 1 ) x n . f(x) = \sum_{n = 0}^{\infty}(n+1)x^n. f(x)=n=0∑∞(n+1)xn.
From the solution above, we have:
1 ( 1 − x ) 2 = ∑ n = 0 ∞ ( n + 1 ) x n . \frac{1}{(1-x)^2} = \sum_{n = 0}^{\infty}(n+1)x^n. (1−x)21=n=0∑∞(n+1)xn.
x 2 ( 1 − x ) 2 = ∑ i = 0 ∞ ( n + 1 ) x n + 2 . \frac{x^2}{(1-x)^2} = \sum_{i = 0}^{\infty}(n+1)x^{n+2}. (1−x)2x2=i=0∑∞(n+1)xn+2.
also
d d x x 2 ( 1 − x ) 2 = ∑ n = 0 ∞ ( n + 2 ) ( n + 1 ) x n + 1 . \frac{d}{dx}\frac{x^2}{(1-x)^2} = \sum_{n = 0}^{\infty}(n+2)(n+1)x^{n+1}. dxd(1−x)2x2=n=0∑∞(n+2)(n+1)xn+1.
since
d d x x 2 ( 1 − x ) 2 = 2 x ( 1 − x ) 3 \frac{d}{dx}\frac{x^2}{(1-x)^2} = \frac{2x}{(1-x)^3} dxd(1−x)2x2=(1−x)32x
2 ( 1 − x ) 3 = ∑ n = 0 ∞ ( n + 2 ) ( n + 1 ) x n \frac{2}{(1-x)^3} = \sum_{n = 0}^{\infty}(n+2)(n+1)x^{n} (1−x)32=n=0∑∞(n+2)(n+1)xn
The closed form of its generated function is:
1 ( 1 − x ) 3 . \frac{1}{(1-x)^3}. (1−x)31.
7. Consider the inequality
x 1 + x 2 + x 3 + x 4 ≤ n x_1 + x_2 + x_3 + x_4 ≤ n x1+x2+x3+x4≤n
where
x 1 , x 2 , x 3 , x 4 , n ⩾ 0 x_1, x_2, x_3, x_4, n \geqslant 0 x1,x2,x3,x4,n⩾0
are all integers.
Suppose also that x 2 ⩾ 2 x_2 \geqslant 2 x2⩾2, x 3 x_3 x3 is a multiple of 4 4 4, and 1 ⩽ x 4 ⩽ 3 1\leqslant x_4 \leqslant 3 1⩽x4⩽3.
Let c n c_n cn be the number of solutions of the inequality subject to these restrictions. Find the generating function for the sequence { c n : n ⩾ 0 } \{c_n : n\geqslant 0\} {cn:n⩾0} and use it to find a closed formula for c n c_n cn.
[Solution]
From the requirements of the problem, in the recurrence function, we will assume that
x 1 = ( 1 + x + x 2 + ⋯ ) = 1 1 − x x_1 = (1+x+x^2+\cdots) = \frac{1}{1-x} x1=(1+x+x2+⋯)=1−x1
x 2 = ( x 2 + x 3 + ⋯ ) = x 2 1 − x x_2 = (x^2+x^3+\cdots) = \frac{x^2}{1-x} x2=(x2+x3+⋯)=1−xx2
x 3 = ( 1 + x 4 + x 8 + ⋯ ) = 1 1 − x 4 x_3 = (1+x^4+x^8+\cdots) = \frac{1}{1-x^4} x3=(1+x4+x8+⋯)=1−x41
x 4 = x + x 2 + x 3 x_4 = x+x^2+x^3 x4=x+x2+x3.
We want x 1 , x 2 , x 3 , x 4 x_1, x_2, x_3, x_4 x1,x2,x3,x4 to add up most to n n n, so we use x 5 = n − x 1 − x 2 − x 3 − x 4 x_5 = n - x_1-x_2-x_3-x_4 x5=n−x1−x2−x3−x4, which is a non-negative integer, represent it in the form of 1 1 − x \frac{1}{1-x} 1−x1.
Then the generating function for the number of the solution will be:
∑ n = 0 ∞ c n x n = C ( x ) = x 3 + x 4 + x 5 ( 1 − x ) 3 ⋅ ( 1 − x 4 ) \sum_{n=0}^{\infty}c_{n}x^n = C(x) = \frac{x^3+x^4+x^5}{(1-x)^3\cdot (1-x^4)} n=0∑∞cnxn=C(x)=(1−x)3⋅(1−x4)x3+x4+x5
where the coefficient of x n x^n xn will be the value of c n c_n cn.
8. What is the generating function for the number of ways to select a group of n n n students from a class of p p p students?
[Solution]
We use x i = ( 1 + x ) x_i = (1+x) xi=(1+x) to describe the status of each student i i i. Therefore:
c n x n = C ( x ) = ( 1 + x ) p c_nx^n = C(x) = (1+x)^{p} cnxn=C(x)=(1+x)p
where the coefficient of x n x^n xn will be the value of c n c_n cn, the number of choices we want.
9. Make up a combinatorial problem (similar to those found in this chapter) that leads to the generating function
( 1 + x 2 + x 4 ) x 2 ( 1 − x ) 3 ( 1 − x 3 ) ( 1 − x 10 ) . \frac{(1+x^2+x^4)x^2}{(1-x)^3(1-x^3)(1-x^{10})}. (1−x)3(1−x3)(1−x10)(1+x2+x4)x2.
[Solution]
从一大堆书中选六种书,总共选取 n n n 本 ( n n n 为正整数),并且要求
所选取的《组合数学》课本数量必须是 10 10 10 的整数倍, 选取的《实变函数》课本数量必须是 3 3 3 的整数倍; 选取的《初等数论》数量只可能是 2 , 4 , 6 2,4,6 2,4,6, 剩下三种书的数量大于等于零。 有多少种选书的方法?
10. Solve the recurrence equation r n + 2 = r n + 1 + 2 r n r_{n+2} = r_{n+1} + 2r_{n} rn+2=rn+1+2rn if r 0 = 1 r_{0} = 1 r0=1 and r 2 = 3 r_2 = 3 r2=3 (Yes, we specify a value for r 2 r_2 r2 but not for r 1 r_1 r1).
[Solution]
The characteristic function of the equation is
q n − q n − 1 − 2 q n − 2 = 0 q^n - q^{n-1} - 2q^{n-2} = 0 qn−qn−1−2qn−2=0
whose roots are
q 1 = 2 , q 2 = − 1. q_1 = 2, q_2 = -1. q1=2,q2=−1.
So its close-form solution is:
q n = C 1 ⋅ ( 2 ) n + C 2 ⋅ ( − 1 ) n . q_n = C_1\cdot (2)^n + C_2\cdot(-1)^n. qn=C1⋅(2)n+C2⋅(−1)n.
From the given conditions of the problem, we have
{ C 1 + C 2 = 1 4 C 1 + C 2 = 3 ⇒ { C 1 = 2 3 C 2 = 1 3 . \begin{cases}C_1 + C_2 = 1 \\ 4C_1 + C_2 = 3 \end{cases} \Rightarrow \begin{cases}C_1 = \frac{2}{3} \\ C_2 = \frac{1}{3}\end{cases}. {C1+C2=14C1+C2=3⇒{C1=32C2=31.
So the solution is displayed as below:
r n = 2 n + 1 + ( − 1 ) n 3 n . r_n = \frac{2^{n+1} +(-1)^n}{3^n}. rn=3n2n+1+(−1)n.
11. Find the general solution of the recurrence equation g n + 2 = 3 g n + 1 − 2 g n g_{n+2} = 3g_{n+1} − 2g_n gn+2=3gn+1−2gn.
[Solution]
The characteristic function of the equation is
q n + 2 − 3 q n − 1 − 2 q n = 0 q^{n+2} - 3q^{n-1} - 2q^{n} = 0 qn+2−3qn−1−2qn=0
whose roots are
q 1 = 2 , q 2 = 1. q_1 = 2, q_2 = 1. q1=2,q2=1.
So its general solution is:
g n = C 1 ⋅ ( 2 ) n + C 2 . g_n = C_1\cdot (2)^n + C_2. gn=C1⋅(2)n+C2.
12. Solve the recurrence equation h n + 3 = 6 h n + 2 − 11 h n + 1 + 6 h n h_{n+3} = 6h_{n+2} - 11h_{n+1} + 6h_n hn+3=6hn+2−11hn+1+6hn if h 0 = 3 , h 1 = 2 h_0 = 3, h_1 = 2 h0=3,h1=2, and h 2 = 4 h_2 = 4 h2=4.
[Solution]
The characteristic function of the equation is
q n + 3 − 6 q n + 2 + 11 q n + 1 − 6 q n = 0 q^{n+3} - 6q^{n+2} + 11q^{n+1} - 6q^{n} = 0 qn+3−6qn+2+11qn+1−6qn=0
whose roots are
q 1 = 1 , q 2 = 2 , q 3 = 3. q_1 = 1, q_2 = 2, q_3 = 3. q1=1,q2=2,q3=3.
So its close-form solution is:
q n = C 1 + C 2 ⋅ 2 n + C 3 ⋅ 3 n . q_n = C_1 + C_2\cdot 2^n + C_3\cdot 3^{n}. qn=C1+C2⋅2n+C3⋅3n.
From the given conditions of the problem, we have
{ C 1 + C 2 + C 3 = 3 C 1 + 2 C 2 + 3 C 3 = 2 C 1 + 4 C 2 + 9 C 3 = 4 ⇒ { C 1 = 6 C 2 = − 5 C 3 = 2 . \begin{cases}C_1 + C_2 +C_3 = 3 \\ C_1 + 2C_2 + 3C_3 = 2 \\ C_1 + 4C_2 + 9C_3 = 4 \end{cases} \Rightarrow \begin{cases}C_1 = 6 \\ C_2 = -5 \\ C_3 = 2\end{cases}. ⎩⎪⎨⎪⎧C1+C2+C3=3C1+2C2+3C3=2C1+4C2+9C3=4⇒⎩⎪⎨⎪⎧C1=6C2=−5C3=2.
So the solution is displayed as below:
q n = 6 − 5 ⋅ 2 n + 2 ⋅ 3 n . q_n = 6 - 5\cdot 2^n + 2\cdot 3^n. qn=6−5⋅2n+2⋅3n.
13. Find the general solutions to each recurrence equation with characteristic polynomial as below:
- ( q − 4 ) 3 ( q + 1 ) ( q − 7 ) 4 ( q − 1 ) = 0 (q-4)^3(q+1)(q-7)^4(q-1) = 0 (q−4)3(q+1)(q−7)4(q−1)=0
- ( q − 5 ) 2 ( q + 5 ) 3 ( q − 1 ) 4 ( q + 1 ) ( q − 4 ) 3 = 0 (q-5)^2(q+5)^3(q-1)^4(q+1)(q-4)^3 = 0 (q−5)2(q+5)3(q−1)4(q+1)(q−4)3=0
[Solution]
-
The roots of the characteristic function is 4 , − 1 , 7 , 1 4, -1, 7, 1 4,−1,7,1 with multiplicity of 3 , 1 , 4 , 1 3, 1, 4, 1 3,1,4,1 respectively.
So it has general solution in the form of
q n = C 1 ⋅ 4 n + C 2 ⋅ n ⋅ 4 n + C 3 ⋅ n 2 ⋅ 4 n + C 4 ⋅ ( − 1 ) n + C 5 ⋅ 7 n + C 6 ⋅ n ⋅ 7 n + C 7 ⋅ n 2 ⋅ 7 n + C 8 ⋅ n 3 ⋅ 7 n + C 9 . q_n = C_1\cdot 4^n + C_2\cdot n\cdot 4^n + C_3\cdot n^2\cdot 4^n + C_4\cdot (-1)^n + C_5\cdot 7^n + C_6 \cdot n\cdot 7^n + C_7 \cdot n^2\cdot 7^n + C_8 \cdot n^3\cdot 7^n + C_9. qn=C1⋅4n+C2⋅n⋅4n+C3⋅n2⋅4n+C4⋅(−1)n+C5⋅7n+C6⋅n⋅7n+C7⋅n2⋅7n+C8⋅n3⋅7n+C9. -
The roots of the characteristic function is 5 , − 5 , 1 , − 1 , 4 5, -5, 1, -1, 4 5,−5,1,−1,4 with multiplicity of 2 , 3 , 4 , 1 , 3 2, 3, 4, 1, 3 2,3,4,1,3 respectively.
So it has general solution in the form of
q n = C 1 ⋅ 5 n + C 2 ⋅ n ⋅ 5 n + { ( − 5 ) n ⋅ ∑ i = 0 2 C i + 3 n i } + ( ∑ i = 0 3 C i + 6 n i ) + C 10 + { ( 4 ) n ⋅ ∑ i = 0 2 C 11 + i n i } . q_n = C_1\cdot 5^n + C_2\cdot n\cdot 5^n + \{(-5)^n\cdot \sum_{i = 0}^{2}C_{i+3} n^{i}\} + (\sum_{i = 0}^{3}C_{i+6}n^{i}) + C_{10} + \{(4)^n\cdot \sum_{i = 0}^{2}C_{11+i}n^{i}\}. qn=C1⋅5n+C2⋅n⋅5n+{(−5)n⋅i=0∑2Ci+3ni}+(i=0∑3Ci+6ni)+C10+{(4)n⋅i=0∑2C11+ini}.
14. 求下列递归方程的通解:
1.1 f n − 3 f n − 1 − 10 f n − 2 = 3 n f_n- 3f_{n-1} - 10f_{n-2} = 3^n fn−3fn−1−10fn−2=3n
1.2 f n − 9 f n − 1 + 27 f n − 2 − 27 f n − 3 = 3 n − 1 f_n - 9f_{n-1} + 27f_{n-2} - 27f_{n-3} = 3n-1 fn−9fn−1+27fn−2−27fn−3=3n−1
15. Let t n t_n tn be the number of ways to tile a 2 ∗ n 2*n 2∗n rectangle using 1 ∗ 1 1*1 1∗1 tiles and L L L-tiles. An L L L-tile is a 2 ∗ 2 2*2 2∗2 tile with the upper-right 1 ∗ 1 1*1 1∗1 square deleted. (An L L L tile may be rotated sothat the “missing” square appears in any of the four positions.)
Find a recursive formula for t n t_n tn along with enough initial conditions to get the recursion started. Use this recursive formula to find a closed formula for t n t_n tn.
16.1 Use generating functions to solve the recurrence equation r n = 4 r n − 1 + 6 r n − 2 r_n = 4r_{n−1} + 6r_{n−2} rn=4rn−1+6rn−2 for n ≥ 2 n ≥ 2 n≥2 with r 0 = 1 r_0 = 1 r0=1 and r 1 = 3 r_1 = 3 r1=3.
16.2 Let b 0 = 1 , b 2 = 2 b_0 = 1, b_2 = 2 b0=1,b2=2, and b 3 = 4 b_3 = 4 b3=4. Use generating functions to solve the recurrence equation b n + 3 = 4 a n + 2 − b n + 1 − 6 a n + 3 n b_{n+3} = 4a_{n+2} − b_{n+1} - 6a_n + 3^n bn+3=4an+2−bn+1−6an+3n for n ≥ 0 n ≥ 0 n≥0.
[Solution]
1.1 该递归方程的齐次方程的特征多项式有特征根: q 1 = − 2 , q 2 = 5. q_1 = -2, q_2 = 5. q1=−2,q2=5.
故齐次部分通解形如
C 1 ⋅ ( − 2 ) n + C 2 ⋅ ( 5 ) n C_1\cdot (-2)^n + C_2\cdot (5)^n C1⋅(−2)n+C2⋅(5)n
设非齐次部分特解为 d ⋅ 3 n d\cdot 3^n d⋅3n. 代入计算得 d = − 9 10 d = -\frac{9}{10} d=−109.
故递归方程的通解为
C 1 ⋅ ( − 2 ) n + C 2 ⋅ ( 5 ) n − 9 10 . C_1\cdot (-2)^n + C_2\cdot (5)^n-\frac{9}{10}. C1⋅(−2)n+C2⋅(5)n−109.
1.2 该递归方程的齐次方程的特征多项式有特征根: q = 3 q=3 q=3, 重数为 3 3 3.
故齐次部分通解形如
( C 1 + C 2 ⋅ n + C 3 ⋅ n 2 ) ⋅ ( 3 ) n . (C_1 + C_2\cdot n + C_3\cdot n^2)\cdot (3)^n. (C1+C2⋅n+C3⋅n2)⋅(3)n.
设非齐次部分特解为 d 1 + d 2 n d_1 + d_2n d1+d2n. 代入计算得 d 1 = − 3 8 , d 2 = − 13 8 . d_1 = -\frac{3}{8}, d_2 = -\frac{13}{8}. d1=−83,d2=−813.
故递归方程的通解为
( C 1 + C 2 ⋅ n + C 3 ⋅ n 2 ) ⋅ ( 3 ) n + ( − 3 8 − 13 8 n ) . (C_1 + C_2\cdot n + C_3\cdot n^2)\cdot (3)^n + (-\frac{3}{8}-\frac{13}{8} n). (C1+C2⋅n+C3⋅n2)⋅(3)n+(−83−813n).
2 要用两种瓦片盖住 n ∗ 2 n*2 n∗2 大小的区域, 有以下几种选择:
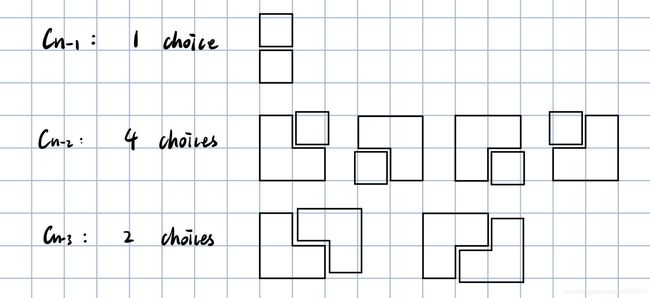
因此, 记 t n t_n tn 为盖住 n ∗ 2 n*2 n∗2 大小的区域的瓦片安放方法数, 可得到以下结论:
{ t n = t n − 1 + 4 t n − 2 + 2 t n − 3 t 0 = 1 , t 1 = 1 , t 2 = 6 , n ⩾ 3. \begin{cases}t_n = t_{n-1} + 4t_{n-2} + 2t_{n-3} \\ t_0 = 1, t_1 = 1, t_2 = 6\end{cases}, ~~~ n\geqslant 3. {tn=tn−1+4tn−2+2tn−3t0=1,t1=1,t2=6, n⩾3.
对于递归方程
− t n + t n − 1 + 4 t n − 2 + 2 t n − 3 = 0 -t_n + t_{n-1} + 4t_{n-2} + 2t_{n-3} = 0 −tn+tn−1+4tn−2+2tn−3=0
其特征多项式的特征根为
q 1 = − 1 , q 2 = 1 − 3 , q 3 = 1 + 3 . q_1 = -1, ~~q_2 = 1-\sqrt{3}, ~~q_3 = 1+\sqrt{3}. q1=−1, q2=1−3, q3=1+3.
故通解形为
C 1 ( − 1 ) n + C 2 ( 1 − 3 ) n + C 3 ( 1 + 3 ) n C_1(-1)^n + C_2(1-\sqrt{3})^n + C_3(1+\sqrt{3})^n C1(−1)n+C2(1−3)n+C3(1+3)n
代入初值条件解得:
C 1 = 2 3 , C 2 = C 3 = 5 6 C_1= \frac{2}{3},~~C_2 = C_3 = \frac{5}{6} C1=32, C2=C3=65.
故通解为
2 3 ( − 1 ) n + 5 6 ( 1 − 3 ) n + 5 6 ( 1 + 3 ) n . \frac{2}{3}(-1)^n + \frac{5}{6}(1-\sqrt{3})^n + \frac{5}{6}(1+\sqrt{3})^n. 32(−1)n+65(1−3)n+65(1+3)n.
