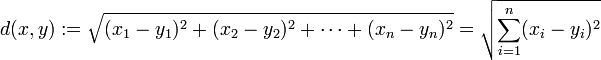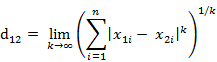浅谈KNN算法原理及python程序简单实现、KD树、球树
最近比较空闲,打算利用这一段时间理一下机器学习的一些常见的算法。第一个是KNN算法:
- KNN
- 1、原理:
KNN,K-NearestNeighbor---K最近邻
K最近邻,就是K个最近的邻居的意思,说的就是每个样本都可以用它最接近的K个邻居来代表。核心思想是如果一个样本在特征空间中的K个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。
KNN算法的结果很大程度上取决于K的选择。
| 如左图所示,有两类不同的样本数据,分别用蓝方块和红三角表示,中间的绿色圆点是待分类的数据。 1、如果K=3,绿色圆点的最近的3个邻居是2个红色小三角形和1个蓝色小正方形,少数从属于多数,基于统计的方法,判定绿色的这个待分类点属于红色的三角形一类。 2、如果K=5,绿色圆点的最近的5个邻居是2个红色三角形和3个蓝色的正方形,还是少数从属于多数,基于统计的方法,判定绿色的这个待分类点属于蓝色的正方形一类。 |
- 2、重要术语:
- 1.算法三要素:
K值得选择、距离度量的方式、分类决策规则
1)K的选择:
没有固定的经验,一般根据样本的分布,选择一个比较小的值,可以通过交叉验证法(简单来说,就是一部分样本做训练集,一部分做测试集)选择一个合适的K值;
选择较小的K值,就相当用较小的邻域中的训练实例进行预测,训练误差会减小,容易发生过拟合;
选择较大的K值,就相当于较大邻域中的训练实例进行预测,其优点是可以减少繁华误差,但缺点是训练误差会增大。
- 2.距离度量:
K近邻算法的核心在于找到实例点的邻居,如何找到邻居,邻居的判定标准是什么?用什么度量?
距离一般使用欧式距离或曼哈顿距离
欧式距离:
是最常见的两点之间或多点之间的距离表示法,如点 x = (x1,...,xn) 和 y = (y1,...,yn) 之间的距离为:
曼哈顿距离:
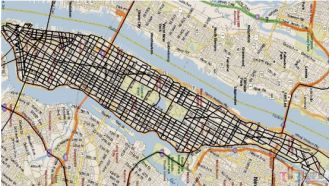
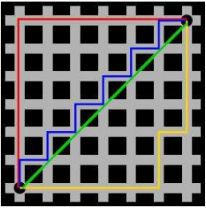
又称为城市街区距离(City Block distance),通俗来讲,想象你在曼哈顿要从一个十字路口开车到另一个十字路口,驾车距离是两点间的直线距离吗?显然不是,除非你能穿越楼。实际驾驶距离就是这个‘曼哈顿距离’,此及曼哈顿距离的来源。
- 二维平面两点a(x1,y1)与b(x2,y2)间的曼哈顿距离 :
![]()
- 两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的曼哈顿距离:
补充:切比雪夫距离:
玩过国际象棋的朋友或许知道,国王走一步能够移动到相邻的8个方格中的任意一个。 那么国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步?。你会发现最少步数总是 max( | x2-x1 | , | y2-y1 | ) 步 。有一种类似的一种距离度量方法叫切比雪夫距离。
(1)二维平面两点a(x1,y1)与b(x2,y2)间的切比雪夫距离:
![]()
(2)两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的切比雪夫距离:
这个公式的另一种等价形式是
- 3.分类决策:
分类:多数表决法
回归:平均值
- KD树(K-dimension tree):
实现K近邻法时,主要考虑的问题是如何对训练数据进行快速K近邻搜索,这点在特征空间的维数大及训练数据容量大时尤为重要。K近邻的最简单实现是线性扫描(也就是我们常说的穷举搜索),这时要计算输入实例与每一个训练实例的距离,当训练集很大时,计算非常耗时,此种方法不可行。
为了提高K近邻搜索的效率,可以考虑使用特殊的结构存储训练数据,以减少计算距离得到次数,就是构建数据索引,因为实际数据一般都会呈现簇状的聚类形态,因此我们想到建立数据索引,然后再进行快速匹配。索引树是一种树结构索引方法,其基本思想是对搜索空间进行层次划分。根据划分的空间是否有混叠可以分为Clipping和Overlapping两种。前者划分空间没有重叠,其代表就是k-d树;后者划分空间相互有交叠,其代表为R树。
建树流程:
KD树是二叉树,表示对K维空间的一个划分。
KD树建树采用的是从m个样本的n维特征中,分别计算n个特征的取值的方差(数据方差大表明沿该坐标轴方向的数据分散的比较开,在这个方向上进行数据分割有较好的分辨率),用方差最大的k维特征nk来作为根节点。选择特征nk取值的中位数nkv对应的样本作为划分点,对于所有的第k维特征的取值小于nkv的样本,划入左子树;对于第k维特征的取值大于或等于nkv的样本,划为右子树,采用和刚才同样的办法找方差最大的特征来做子节点,递归的生成KD树。
对于n个实例的k维数据来说,建立kd-tree的时间复杂度为O(k*n*logn)。
| 举个例子:
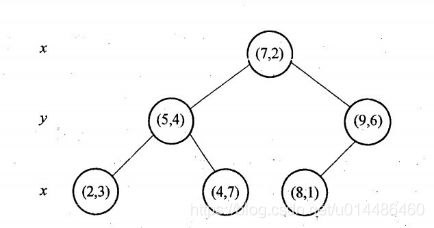
6个二维数据点{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}构建kd树的具体步骤为:
如上算法所述,kd树的构建是一个递归过程,我们对左子空间和右子空间内的数据重复根节点的过程就可以得到一级子节点(5,4)和(9,6),同时将空间和数据集进一步细分,如此往复直到空间中只包含一个数据点。 与此同时,经过对上面所示的空间划分之后,我们可以看出,点(7,2)可以为根结点,从根结点出发的两条红粗斜线指向的(5,4)和(9,6)则为根结点的左右子结点,而(2,3),(4,7)则为(5,4)的左右孩子(通过两条细红斜线相连),最后,(8,1)为(9,6)的左孩子(通过细红斜线相连)。如此,便形成了下面这样一棵k-d树:
|
KD树搜索最近邻:
首先在KD树里面找到包含目标点的叶子结点。
以目标点为圆心,以目标点到叶子结点样本实例的距离为半径,得到一个超球体,最近邻的点一定在这个超球体内部。
然后返回叶子结点的父节点,检查另一个子节点包含的超矩形体是否和超球体相交,如果相交就到这个子节点寻找是否有更加近的近邻,有的话就更新最近邻。
如果不相交那就简单了,直接返回父节点的父节点,在另一个子树继续搜索最近邻。
当回溯到根节点时,算法结束,此时保存的最近邻结点就是最终的最近邻。
| 举个例子:
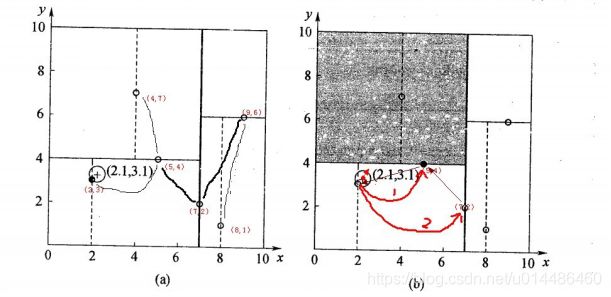
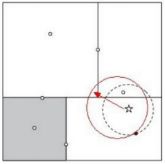
星号表示要查询的点(2.1,3.1)。通过二叉搜索,顺着搜索路径很快就能找到最邻近的近似点,也就是叶子节点(2,3)。而找到的叶子节点并不一定就是最邻近的,最邻近肯定距离查询点更近,应该位于以查询点为圆心且通过叶子节点的圆域内。为了找到真正的最近邻,还需要进行相关的‘回溯'操作。也就是说,算法首先沿搜索路径反向查找是否有距离查询点更近的数据点。 以查询(2.1,3.1)为例:
第二个例子: 一个复杂点了例子如查找点为(2,4.5),具体步骤依次如下:
上述两次实例表明,当查询点的邻域与分割超平面两侧空间交割时,需要查找另一侧子空间,导致检索过程复杂,效率下降。
|
优缺点
KD树提高了KNN搜索的效率,但是在某些时候效率并不高,比如当处理不均匀分布的数据集时,不管是近似方形还是矩形,甚至正方形,都不是最好的形状,因为他们都有角,
例如
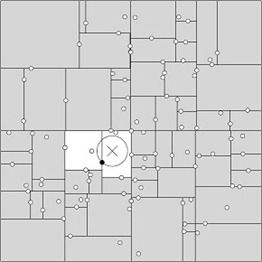
| 一般来讲,最临近搜索只需要检测几个叶子结点即可,如下图所示: 但是,如果当实例点的分布比较糟糕时,几乎要遍历所有的结点,如下所示: 研究表明N个节点的K维k-d树搜索过程时间复杂度为:tworst=O(kN1-1/k)。 同时,以上为了介绍方便,讨论的是二维或三维情形。但在实际的应用中,如SIFT特征矢量128维,SURF特征矢量64维,维度都比较大,直接利用k-d树快速检索(维数不超过20)的性能急剧下降,几乎接近贪婪线性扫描。假设数据集的维数为D,一般来说要求数据的规模N满足N»2D,才能达到高效的搜索。所以这就引出了一系列对k-d树算法的改进:BBF算法,和一系列M树、VP树、MVP树等高维空间索引树(下文2.6节kd树近邻搜索算法的改进:BBF算法,与2.7节球树、M树、VP树、MVP树)。
|
KD树 球树
- 球树:
球树,顾名思义就是分割块都是超球体,而不是KD树里面的超矩形体。
建树流程:
先构造一个超球体,此超球体是可以包含所有样本的最小球体;
从球中选择一个离球的中心点最远的点,然后选择第二个点离第一个点最远,将球中所有的点分配到离这两个聚类中心最近的一个上,然后计算每个聚类的中心,以及聚类能够包含它所有数据点所需的最小半径。这样得到了两个子超球体,和KD树里面的左右字数对应。
对于这两个超球体,递归执行上一步骤,最终得到一个球树。
球树搜索最近邻:
首先自上而下贯穿整棵树找出包含目标点所在的叶子,并在这个球里找出与目标点最近邻的点,这将确定出目标点距离它的最近邻点的一个上限值,然后跟KD树查找一样,检查兄弟结点,如果目标结点到兄弟结点中心的距离超过兄弟结点的半径与当前的上限之和,那么兄弟结点里不可能存在一个更近的点,否则的话,必须进一步检查位于兄弟结点下的子树。
检查完兄弟结点后,我们向父节点回溯,继续搜索最小邻近值。当回溯到根节点时,此时的最小邻近值就是最终的搜素结果。
- 3、优缺点:
KNN的主要优点:
思想简单,既可以做分类又可以做回归;
可用于非线性分类;
训练时间复杂度比支持向量机之类的算法低,仅为O(n);
和朴素贝叶斯之类的算法比,对数据没有假设,准确度高,对异常点不敏感;
对类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合;
比较适用于样本比较大的类域的自动分类,而那些样本容量比较小的类域采用这种算法容易产生误分。
KNN主要缺点:
计算量大,尤其是特征数非常多的时候;
样本不平衡时,对稀有类别的预测准确率低;
KD树,球树之类的模型建立需要大量的内存;
使用懒惰的学习方法,基本不学习,导致预测时的速度比逻辑回归之类的算法慢;
比起决策树模型,KNN模型的可解释性不强。
- 4、KNN算法的简单实现
"""
给定一组样本集("dataset.txt"),数据如下:
1 2 A
1 1 A
1.5 1.5 A
2 1 A
2 2 B
3 2 B
3 3 B
4 3 B
请使用knn算法 预测 2 2.5的类型
实现思路:
1.将预测的点 和样本中所有点 进行距离计算
2.对距离进行排序
3.选择前k个距离
4.计算前k个最近距离的点的分类个数
5.返回类别个数最多的分类
"""
#法1:
import numpy as np
import operator
def loadData(filename):
return np.loadtxt(filename,dtype=np.str,delimiter=",")
def knn(dataset,testData,k):
x = dataset[:, :-1].astype(np.float)
y = dataset[:, -1]
# print(x,y)
#1.将预测的点 和样本中所有点 进行距离计算
distance = np.sum((x-testData)**2,axis=1)**0.5
#2.对距离进行排序
sortedIndex = np.argsort(distance)
# 3.选择前k个距离
# 4.计算前k个最近距离的点的分类个数
classLabel={}
for i in range(k):
label = y[sortedIndex[i]]
classLabel[label]=classLabel.get(label,0)+1
print(sortedIndex)#[4 0 2 5 6 3 1 7]
#5.返回类别个数最多的分类
# print(sorted(classLabel.items(),key=operator.itemgetter(1),reverse=True))#[('A', 2), ('B', 1)]
return sorted(classLabel.items(),key=operator.itemgetter(1),reverse=True)[0][0]
if __name__=="__main__":
dataset = loadData("dataset.txt")
testData=[2,2.5]
result = knn(dataset,testData,3)
print(result)#A
################################################################
#法2:
import numpy as np
import pandas as pd
df=pd.DataFrame([[1,2],[1,1],[1.5,1.5],[2,1],[2,2],[3,2],[3,3],[4,3]],
index=["A","A","A","A","B","B","B","B"])
sub_= np.tile([2,2.5], (8, 1))-df
square_=sub_**2
add_=square_.sum(axis=1)
distance=add_**0.5
sort_=np.sort(distance)
argsort_=np.argsort(distance)
k=3
near_distance=distance[np.argsort(distance)[:k]]
print(near_distance)
"""
运行结果:
B 0.500000
A 1.118034
A 1.118034
dtype: float64
"""
num_a=near_distance.loc["A"].size
num_b=near_distance.loc["B"].size
k_label=np.where(num_a>num_b,"A","B")
print(k_label)#A- 5、sklearn库包调用
-
from sklearn.neighbors import KNeighborsClassifier import numpy as np dataset = np.loadtxt("dataset.txt",dtype=np.str,delimiter=",") x = dataset[:, :-1].astype(np.float) y = dataset[:, -1] #建立学习模型 #指定k的个数 model = KNeighborsClassifier(n_neighbors=3) #训练模型 model.fit(x,y) #预测 testData = [[2, 2.5]] result = model.predict(testData) print(result)#['A'] #输出预测类别的概率是多少 print(model.predict_proba(testData))#[[0.66666667 0.33333333]]本人能力有限,欢迎指正。