回归算法之线性回归
线性回归的定义是:目标值预期是输入变量的线性组合。线性模型形式简单、易于建模,但却蕴含着机器学习中一些重要的基本思想。线性回归,是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,运用十分广泛。
优点:结果易于理解,计算不复杂
缺点:对非线性的数据拟合不好
适用数据类型:数值型和标称型
对于单变量线性回归,例如:前面房价例子中房子的大小预测房子的价格。f(x) = w1*x+w0,这样通过主要参数w1就可以得出预测的值。
通用公式为:
h\left(\theta\right){=}\theta_0+\theta_1{x}h(θ)=θ0+θ1x
那么对于多变量回归,例如:瓜的好坏程度 f(x) = w0+0.2色泽+0.5根蒂+0.3*敲声,得出的值来判断一个瓜的好与不好的程度。
通用公式为:
h\left(\theta\right){=}\theta_{0}+\theta_{1}{x_{1}}+\theta_{2}{x_{2}}h(θ)=θ0+θ1x1+θ2x2
线性模型中的向量W值,客观的表达了各属性在预测中的重要性,因此线性模型有很好的解释性。对于这种“多特征预测”也就是(多元线性回归),那么线性回归就是在这个基础上得到这些W的值,然后以这些值来建立模型,预测测试数据。简单的来说就是学得一个线性模型以尽可能准确的预测实值输出标记。
那么如果对于多变量线性回归来说我们可以通过向量的方式来表示W值与特征X值之间的关系:
\theta = \begin{pmatrix}\theta_0 \\\theta_1 \\\theta_2 \\\theta_3\end{pmatrix}θ=⎝⎜⎜⎛θ0θ1θ2θ3⎠⎟⎟⎞ X = \begin{pmatrix}x_0\\x_1\\x_2\\x_3\end{pmatrix}X=⎝⎜⎜⎛x0x1x2x3⎠⎟⎟⎞
两向量相乘,结果为一个整数是估计值,其中所有特征集合的第一个特征值x_0x0=1,那么我们可以通过通用的向量公式来表示线性模型:
h(\theta) = \theta^T * xh(θ)=θT∗x
一个列向量的转置与特征的乘积,得出我们预测的结果,但是显然我们这个模型得到的结果可定会有误差,如下图所示:
单变量
多变量
损失函数
损失函数是一个贯穿整个机器学习重要的一个概念,大部分机器学习算法都会有误差,我们得通过显性的公式来描述这个误差,并且将这个误差优化到最小值。
对于线性回归模型,将模型与数据点之间的距离差之和做为衡量匹配好坏的标准,误差越小,匹配程度越大。我们要找的模型就是需要将f(x)和我们的真实值之间最相似的状态。于是我们就有了误差公式,模型与数据差的平方和最小:
J\left(\theta\right){=}\sum_{i=1}^{m} \left({h_\theta}({x}^{(i)}){-}{y}^{(i)}\right)^{2}J(θ)=∑i=1m(hθ(x(i))−y(i))2
上面公式定义了所有的误差和,那么现在需要使这个值最小?那么有两种方法,一种使用梯度下降算法,另一种使正规方程解法(只适用于简单的线性回归)。
梯度下降算法
上面误差公式是一个通式,我们取两个单个变量来求最小值,误差和可以表示为:
cost\left({w_0+w_1x_1}\right){=}\sum_{i=1}^{N} \left({w_0+w_1x_i}{-}{y_i}\right)^{2}cost(w0+w1x1)=∑i=1N(w0+w1xi−yi)2
可以通过调整不同的w_1w1和w_0w0的值,就能使误差不断变化,而当你找到这个公式的最小值时,你就能得到最好的w_1w1,w_0w0 而这对\left({w_1},{w_0}\right)(w1,w0)就是能最好描述你数据关系的模型参数。
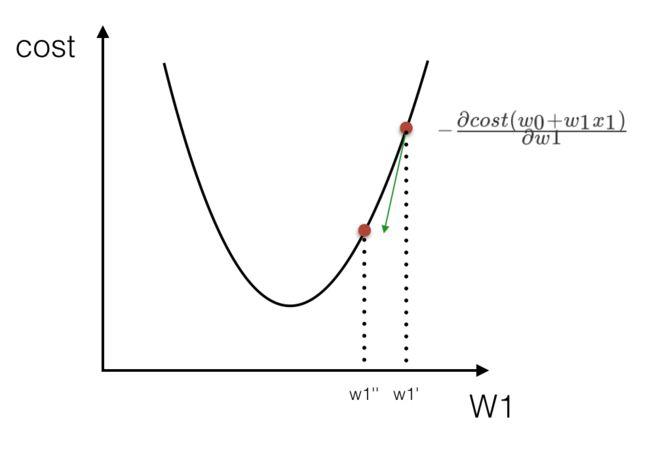
怎么找cost\left({w_0+w_1x_1}\right)cost(w0+w1x1)的最小? cost\left({w_0+w_1x_1}\right)cost(w0+w1x1)的图像其实像一个山谷一样,有一个最低点。找这个最低点的办法就是,先随便找一个点(w_1w1=5, w_0w0=4), 然后 沿着这个碗下降的方向找,最后就能找到山谷的最低点。
所以得出{w_1^{''}}-{w_1^{'}}=-\frac{\partial{cost\left({w_0+w_1x_1}\right)}}{\partial w1}w1′′−w1′=−∂w1∂cost(w0+w1x1),那么这个过程是按照某一点在w_1w1上的偏导数下降寻找最低点。当然在进行移动的时候也需要考虑,每次移动的速度,也就是\alphaα的值,这个值也叫做(学习率),如下式:
{w_1}:=-{w_1}-\alpha\frac{\partial{cost\left({w_0+w_1x_1}\right)}}{\partial w1}w1:=−w1−α∂w1∂cost(w0+w1x1)
{w_0}:=-{w_0}-\alpha\frac{\partial{cost\left({w_0+w_1x_1}\right)}}{\partial w1}w0:=−w0−α∂w1∂cost(w0+w1x1)
这样就能求出w_0,w_1w0,w1的值,当然你这个过程是不断的进行迭代求出来,通过交叉验证方法即可。
LinearRegression
sklearn.linear_model.LinearRegression
class LinearRegression(fit_intercept = True,normalize = False,copy_X = True,n_jobs = 1)
"""
:param normalize:如果设置为True时,数据进行标准化。请在使用normalize = False的估计器调时用fit之前使用preprocessing.StandardScaler
:param copy_X:boolean,可选,默认为True,如果为True,则X将被复制
:param n_jobs:int,可选,默认1。用于计算的CPU核数
"""实例代码:
from sklearn.linear_model import LinearRegression
reg = LinearRegression()
方法
fit(X,y,sample_weight = None)
使用X作为训练数据拟合模型,y作为X的类别值。X,y为数组或者矩阵
reg.fit ([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
predict(X)
预测提供的数据对应的结果
reg.predict([[3,3]])
array([ 3.])
属性
coef_
表示回归系数w=(w1,w2....)
reg.coef_
array([ 0.5, 0.5])
intercept_ 表示w0
加入交叉验证
前面我们已经提到了模型的交叉验证,那么我们这个自己去建立数据集,然后通过线性回归的交叉验证得到模型。由于sklearn中另外两种回归岭回归、lasso回归都本省提供了回归CV方法,比如linear_model.Lasso,交叉验证linear_model.LassoCV;linear_model.Ridge,交叉验证linear_model.RidgeCV。所以我们需要通过前面的cross_validation提供的方法进行k-折交叉验证。
from sklearn.datasets.samples_generator import make_regression
from sklearn.model_selection import cross_val_score
from sklearn import linear_model
import matplotlib.pyplot as plt
lr = linear_model.LinearRegression()
X, y = make_regression(n_samples=200, n_features=5000, random_state=0) result = cross_val_score(lr, X, y) print result