语义分割——U-Net

本案例我们将主要介绍关于语义分割的应用，一个图像分类任务和关于这个任务的特定算法。之后还会对我最近所做的一些案例进行一些介绍。

目录

简介

1 语义分割与实体分割

2 案例研究：Data Science Bowl 2018

下降模块

3 迁移学习

4 动态U-Net

---

简介

根据定义，语义分割是将图像分割成不同的部分，每个部分代表一个实体。例如，我们对图片中的像素进行分类，这个像素可能属于一个人、一辆车、一棵树或数据集里的任何其他实体。

1 语义分割与实体分割

与它的老大哥实体分割相比，语义分割相对容易一些。

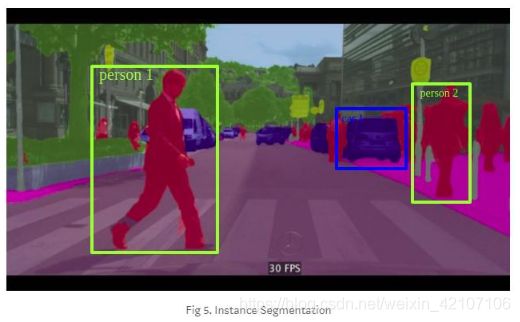
在实体分割中，我们的目标不仅是对人、汽车或树进行像素级别的预测，而且还能够识别出每个类别下的每个实体，如人物1、人物2、树1、树2、汽车1、汽车2、汽车3等等。目前实体分割算法中最出色的就是Mask R-CNN。这个算法有两个阶段，由多个子网络构成：RPN（区域推荐网络），FPN（特征金字塔网络）和FCN（全卷积网络）。

 

 

2 案例研究：Data Science Bowl 2018

Data Science Bowl 2018刚刚结束，我从中学到了很多东西。其中最重要的一课就是数据预处理和后处理对机器学习甚至深度学习的结果都有着至关重要的影响。这对我们如很根据问题建立模型非常重要。

我将会对夺冠组的模型与本案例的相关部分进行简要介绍。

Data Science Bowl 2018的任务是识别给定图片中的细胞核并针对每个细胞核生成一个滤镜。

现在让我们来思考一下要解决这个问题我们需要使用语义分割还是实体分割呢？

下面是一张加了滤镜和未加滤镜的样图：

 

这个问题可能一听起来像是一个语义分割问题，但它实际上是一个实体分割问题。我们需要分别识别出图片中每个细胞的细胞核，就像前面例子中要识别出人物1、人物2、树1、树2、汽车1、汽车2、汽车3等等一样。也许这项任务的动机是随着时间的推移，从细胞样本中追踪细胞核的大小、数量和特征。这一追踪过程的自动化能够提高疾病治疗方案研发的速度。

或许你现在会想问本案例的题目是语义分割，那为什么还会在这里浪费篇章讲解一个实体分割的案例呢？确实，这是一个实体分割的案例，但是后面你会看到我们如何将这个实体分割问题转化为以多类别语义分割问题。

在Data Science Bowl 2018三个月的比赛过程中只有两个模型被大家广泛讨论应用：Mask-RNN和U-Net。如我之前所说的那样Mask-RNN是当今实体识别最优秀的算法之一。它可以探测出每个个体并预测它们使用的滤镜。但是由于采用了包含两个阶段的学习方法，Mask-RNN的实现和训练非常困难。你需要先训练一个RPN（区域推荐网络）然后在对边界框，类别和滤镜进行预测。

而U-Net是一种非常流行的用于语义分割的端到端编码解码器网络。它最早被用于生物医学图片分割，与Data Science Bowl 2018中的任务非常相似。现在我们来详细地学习一下U-Net。

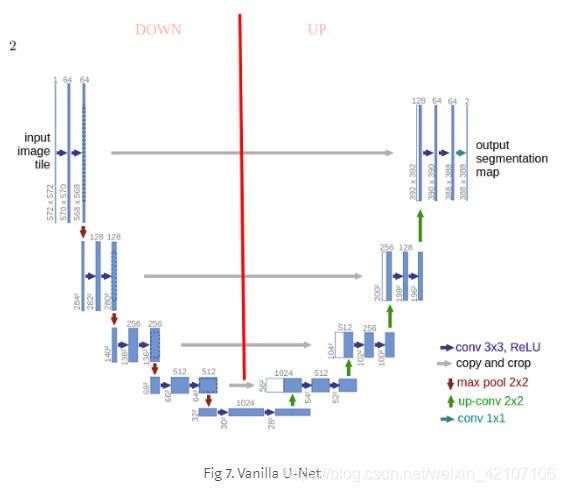
让我们从网络结构开始学吧。

 

对之前学习过卷积神经网络的读者来说，这部分学习起来应该不难。上图中的第一部分被称为下降部分（down），或者你可以把它理解为用卷积块和最大值池化下采样从不同层次上对输入图像特征进行提取。

网络的第二部分包括上采样、链接和常规的卷积操作。CNN上采样或许对许多读者来说是一个新概念。但是它不难理解：即扩张特征图的维度使其与左边的链接块维度相同。你可以看到图中的灰色和绿色箭头代表的就是我们将两个特征图链接在一起的过程。与其他完全卷积性分割网络相比，U-Net的主要贡献在于，当我们在网络上进行采样和深入的时候，我们将下降部分高分辨率特征与上采样特征连接在一起，以便使接下来的卷积过程更好地进行特征集中化和特征学习表示。由于上采样是一种扩散的操作，所以我们需要在前面的阶段中进行良好的特征集中化表示。与上面相似的同层级融合的思想同样在FPN（特征金字塔网络）中也有。

我们可以将下降操作中的一个模块定义为：卷积+下采样。

下降模块

def make_conv_bn_relu(in_channels, out_channels, kernel_size=3, stride=1, padding=1):
    return [
        nn.Conv2d(in_channels, out_channels, kernel_size=kernel_size,  stride=stride, padding=padding, bias=False),
        nn.BatchNorm2d(out_channels),
        nn.ReLU(inplace=True)
    ]
self.down1 = nn.Sequential(
    *make_conv_bn_relu(in_channels, 64, kernel_size=3, stride=1, padding=1 ),
    *make_conv_bn_relu(64, 64, kernel_size=3, stride=1, padding=1 ),
)

# 卷积后的最大值下采样
down1 = self.down1(x)
out1   = F.max_pool2d(down1, kernel_size=2, stride=2)

类似的我们可以将上升操作的一个模块定义为：上采样+链接+卷积。

import torch
import torch.nn as nn
# 上升模块
def make_conv_bn_relu(in_channels, out_channels, kernel_size=3, stride=1, padding=1):
    return [
        nn.Conv2d(in_channels, out_channels, kernel_size=kernel_size,  stride=stride, padding=padding, bias=False),
        nn.BatchNorm2d(out_channels),
        nn.ReLU(inplace=True)
    ]
self.up4 = nn.Sequential(
    *make_conv_bn_relu(128,64, kernel_size=3, stride=1, padding=1 ),
    *make_conv_bn_relu(64,64, kernel_size=3, stride=1, padding=1 )
)
self.final_conv = nn.Conv2d(32, num_classes, kernel_size=1, stride=1, padding=0 )

# upsample out_last, concatenate with down1 and apply conv operations
out   = F.upsample(out_last, scale_factor=2, mode='bilinear')  
out   = torch.cat([down1, out], 1)
out   = self.up4(out)

# final 1x1 conv for predictions
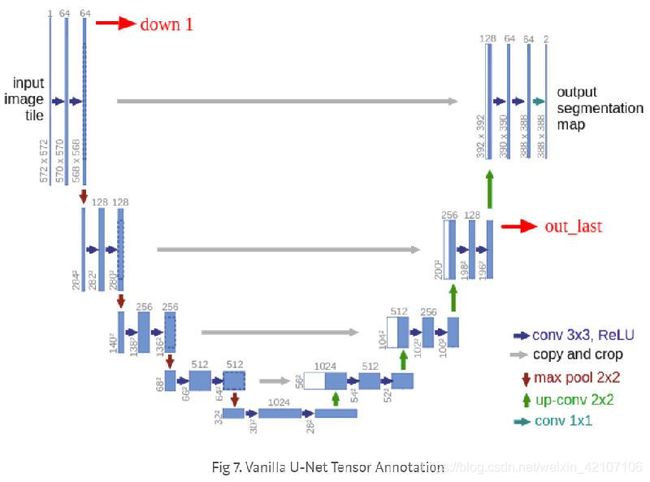
final_out = self.final_conv(out)

仔细看上图的第一层，您可能会注意到输出维度（388 x 388）与原始输入（572 x 572）不一样。如果想要得到一致的大小，可以应用填充卷积来使链接两端的数据一致，就像我们在上面的示例代码中所做的那样。

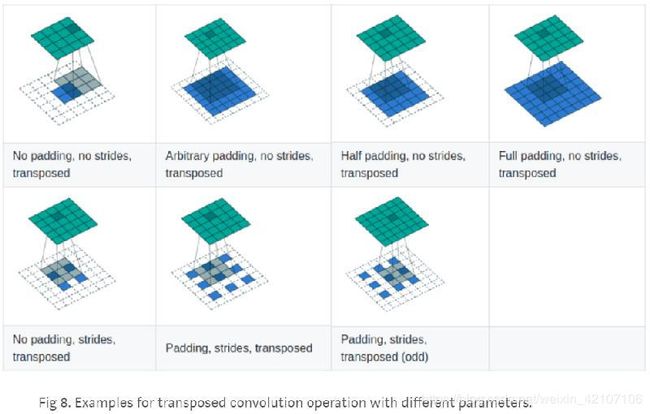
当提到上采样时你一定会遇到反卷积这个词。但实际上我们在上采样过程中所进行的是普通的卷积而非反卷积。下面让我们由浅入深来介绍一下上采样。实际上在PyTorch中对于一个2D的张量有三种反卷积的方式：

临近采样法

这是我们寻找图片中丢失像素值最简单的方法。它同时能扩大张量的尺寸，如：2∗2,4∗4,5∗5,6∗62∗2,4∗4,5∗5,6∗6。

让我们通过NumPy来实现一下这个简单的算法吧。

import numpy as np
import datetime
import math
import os
import random
import re
from collections import Counter

A=np.array([[1,2],[3,4]])
# def nn_interpolate(A, new_size):
#     """
#     Nearest Neighbor Interpolation, Step by Step
#     """
#     # get sizes
#     old_size = A.shape
    
#     # calculate row and column ratios
#     row_ratio, col_ratio = new_size[0]/old_size[0], new_size[1]/old_size[1]
    
#     # define new pixel row position i
#     new_row_positions = np.array(range(new_size[0]))+1
#     new_col_positions = np.array(range(new_size[1]))+1
    
#     # normalize new row and col positions by ratios
#     new_row_positions = new_row_positions / row_ratio
#     new_col_positions = new_col_positions / col_ratio
    
#     # apply ceil to normalized new row and col positions
#     new_row_positions = np.ceil(new_row_positions)
#     new_col_positions = np.ceil(new_col_positions)
    
#     # find how many times to repeat each element
#     row_repeats = np.array(list(Counter(new_row_positions).values()))
#     col_repeats = np.array(list(Counter(new_col_positions).values()))
    
#     # perform column-wise interpolation on the columns of the matrix
#     row_matrix = np.dstack([np.repeat(A[:, i], row_repeats) 
#                             for i in range(old_size[1])])[0]
    
#     # perform column-wise interpolation on the columns of the matrix
#     nrow, ncol = row_matrix.shape
#     final_matrix = np.stack([np.repeat(row_matrix[i, :], col_repeats)
#                              for i in range(nrow)])

#     return final_matrix
    
    
def nn_interpolate(A, new_size):
    """Vectorized Nearest Neighbor Interpolation"""

    old_size = A.shape
    row_ratio, col_ratio = np.array(new_size)/np.array(old_size)

    # row wise interpolation 
    row_idx = (np.ceil(range(1, 1 + int(old_size[0]*row_ratio))/row_ratio) - 1).astype(int)

    # column wise interpolation
    col_idx = (np.ceil(range(1, 1 + int(old_size[1]*col_ratio))/col_ratio) - 1).astype(int)

    final_matrix = A[:, row_idx][col_idx, :]

    return final_matrix

print ('A:',A)
print ('nn_interpolate 4*4:',nn_interpolate(A,(4,4)))
print ('nn_interpolate 5*5:',nn_interpolate(A,(5,5)))
print ('nn_interpolate 6*6:',nn_interpolate(A,(6,6)))

A: [[1 2]
 [3 4]]
nn_interpolate 4*4: [[1 1 2 2]
 [1 1 2 2]
 [3 3 4 4]
 [3 3 4 4]]
nn_interpolate 5*5: [[1 1 2 2 2]
 [1 1 2 2 2]
 [3 3 4 4 4]
 [3 3 4 4 4]
 [3 3 4 4 4]]
nn_interpolate 6*6: [[1 1 1 2 2 2]
 [1 1 1 2 2 2]
 [1 1 1 2 2 2]
 [3 3 3 4 4 4]
 [3 3 3 4 4 4]
 [3 3 3 4 4 4]]

下面我们来看看通过PyTorch工具包实现的方法：

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torch.utils.data
from torch.autograd import Variable

input = Variable(torch.randn(1, 1, 2, 2))

torch.nn.functional.interpolate(input, size=None, scale_factor=2, mode='nearest', align_corners=None)

tensor([[[[ 0.6189,  0.6189, -1.1320, -1.1320],
          [ 0.6189,  0.6189, -1.1320, -1.1320],
          [ 0.7668,  0.7668, -1.0094, -1.0094],
          [ 0.7668,  0.7668, -1.0094, -1.0094]]]])

双线性插值法

双线性插值法的计算效率要比临近采样法的计算效率低一些但是准确率会更高。一个像素值是其他像素值基于到这个像素距离的加权平均。下面是在PyTorch中的实现方法:

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torch.utils.data
from torch.autograd import Variable

input = Variable(torch.randn(1, 1, 2, 2))

#m=nn.Upsample(scale_factor=2, mode='bilinear')
torch.nn.functional.interpolate(input, size=None, scale_factor=2, mode='bilinear', align_corners=False)
#print (m(input))

tensor([[[[ 1.3508,  1.0817,  0.5434,  0.2743],
          [ 1.0107,  0.7676,  0.2815,  0.0385],
          [ 0.3306,  0.1396, -0.2423, -0.4333],
          [-0.0095, -0.1744, -0.5042, -0.6691]]]])

反卷积法

反卷积法中的权重是通过反向传播算法学习得到的。

import torch
import torch.nn as nn
import torch.optim as optim
import torch.utils.data
from torch.autograd import Variable

input = Variable(torch.randn(1, 16, 12, 12))
downsample = nn.Conv2d(16, 16, 3, stride=2, padding=1)
upsample = nn.ConvTranspose2d(16, 16, 3, stride=2, padding=1)
h = downsample(input)
output = upsample(h, output_size=input.size())
print (output)

 

tensor([[[[-0.1221, -0.0161, -0.0493,  ...,  0.0017,  0.0744,  0.0004],
          [-0.0439, -0.3035,  0.0137,  ...,  0.3248, -0.1134, -0.0397],
          [-0.0159,  0.0045,  0.0357,  ..., -0.1156,  0.2106, -0.0238],
          ...,
          [ 0.0582, -0.3238,  0.0078,  ...,  0.0153, -0.1320, -0.0278],
          [-0.1077, -0.3365, -0.1929,  ..., -0.2388,  0.1175, -0.1195],
          [-0.0200, -0.0574, -0.2075,  ...,  0.0980, -0.1903,  0.0330]],

         [[ 0.2800,  0.2799,  0.1046,  ..., -0.0655, -0.1452, -0.1874],
          [-0.0921,  0.0928, -0.1436,  ..., -0.1787,  0.0577, -0.0276],
          [-0.0618,  0.1316,  0.1878,  ...,  0.0990,  0.0396, -0.0718],
          ...,
          [ 0.0832,  0.3933,  0.1041,  ...,  0.0144,  0.0331,  0.0043],
          [ 0.0970,  0.2244,  0.3404,  ..., -0.1697,  0.1295,  0.1027],
          [ 0.0891,  0.2180,  0.1309,  ...,  0.1633,  0.0072, -0.0333]],

         [[-0.2146,  0.0164, -0.0361,  ...,  0.0447,  0.0043, -0.0197],
          [-0.0170,  0.1240,  0.1030,  ..., -0.0848, -0.1780,  0.0481],
          [ 0.1325,  0.1914, -0.0096,  ..., -0.1029, -0.0598, -0.2478],
          ...,
          [-0.2754, -0.0551,  0.1325,  ..., -0.1874, -0.0202,  0.3443],
          [-0.0458, -0.3709,  0.0338,  ..., -0.1914, -0.1292, -0.1430],
          [-0.0944, -0.3503,  0.1163,  ..., -0.3890, -0.0880, -0.1133]],

         ...,

         [[ 0.0623,  0.0937,  0.0380,  ..., -0.1333,  0.1603,  0.1729],
          [ 0.0253,  0.2001,  0.0264,  ...,  0.1863,  0.0354, -0.1174],
          [ 0.1437, -0.0333,  0.0211,  ...,  0.0194, -0.1282, -0.0217],
          ...,
          [ 0.1351,  0.0534, -0.0090,  ...,  0.2875,  0.0552,  0.1721],
          [ 0.0909,  0.3132, -0.1537,  ...,  0.0339, -0.1507,  0.0275],
          [ 0.1495,  0.0921,  0.2036,  ..., -0.1507,  0.1580, -0.0871]],

         [[-0.0518, -0.2970,  0.0922,  ..., -0.0004, -0.0495,  0.1527],
          [ 0.2152,  0.0652, -0.0242,  ...,  0.3037,  0.0036, -0.0457],
          [ 0.0186,  0.2136,  0.0253,  ..., -0.1687, -0.0459,  0.1228],
          ...,
          [-0.1156,  0.0567, -0.0972,  ...,  0.0175,  0.0271, -0.0649],
          [-0.0248, -0.3832,  0.1296,  ...,  0.1609, -0.0071,  0.0622],
          [ 0.2020, -0.0142,  0.1541,  ..., -0.1017,  0.2107,  0.0040]],

         [[-0.0681, -0.1360, -0.1161,  ...,  0.0595, -0.0956, -0.2600],
          [-0.2344, -0.0899, -0.1187,  ...,  0.0824, -0.0724, -0.0495],
          [-0.0494, -0.1168, -0.1699,  ...,  0.2432, -0.1861, -0.1158],
          ...,
          [ 0.0592, -0.4151,  0.1063,  ..., -0.3050, -0.0800, -0.0293],
          [ 0.0269, -0.0313, -0.0397,  ..., -0.1916, -0.2175, -0.1452],
          [-0.0310,  0.0361, -0.1790,  ..., -0.2915, -0.0074,  0.0373]]]],
       grad_fn=)

以上我们已经介绍了PyTorch中的三种上采样方法，在实际问题中我们需要根据实际的条件进行算法的选择。反卷积法相对较为灵活，提供了许多可以设置的参数，而另外两种算法更为简单，计算效率更高。

现在让我们来重新看看我们的案例。在这个案例中最大的问题就是Vanilla U-Net在识别重叠的细胞的细胞核时效果不是很好。当细胞距离较远时你可以为每个细胞设立一个目标二进制滤镜让U-Net来学习，但当许多细胞重叠在一起或距离很近时它们就得共用一个滤镜了从而很难分开这些细胞。

 在解决这个问题时，U-Net论文的作者使用了加权交叉熵来增强细胞边界的学习。这种方法帮助他们分离重叠的细胞。其基本的想法是增加细胞边界的权重，使网络增强对细胞间隙的学习。

解决这类问题的另一种方法是将二进制滤镜转换成多类目标。U-Net的好处在于，您可以通过在最后一层使用1*1的卷积来构造您的网络来输出尽任意多的通道，并在用不同通道的输出表示不同类别。

在做出这些预测之后，像分水岭这样的经典图像处理算法可以用于后期处理，从而进一步细分单个细胞核。

 

3 迁移学习

到目前为止，我们已经讲解了如何定义了普通U-Net的模块，以及如何控制目标来进行实体分割。现在我们可以进一步讨论这类编码-解码网络的灵活性。这里的灵活性是指对网络的改造和创新。

相信学习过深度学习的读者一定听说过迁移学习吧。迁移学习(Transfer learning) 顾名思义就是在缺少训练样本时把已学训练好的模型参数迁移到新的模型来帮助新模型训练。即使有足够的数据，迁移学习也可以在一定程度上提高性能。它不仅可应用于计算机视觉任务，而且也适用于NLP任务。

迁移学习被证明同样适用于像U-Net这样结构的网络。我们之前把U-Net分为两部分：上升部分和下降部分。现在我们重新将这两部分命名为编码器和解码器。编码器部分可以在一个低维度的特征空间中表示我们的输入。现在想象用ImageNet，VGG，ResNet，Inception，NasNet等你喜欢的网络来替换这个编码器。这些网络都是用来做一件普通的事情：用最好的方式对自然图像进行编码来对其分类。

所以为什么不使用以上其中一个架构作为我们的编码器然后使用与U-Net一样解码器来构造我们的模型呢？

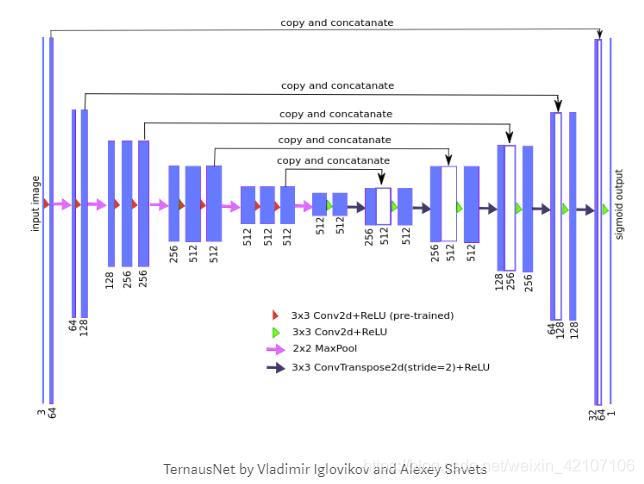
Kaggle Carvana的赢家TernausNet就用了迁移的思想把VGG11作为它的编码器。

 

4 动态U-Net

受TernausNet和许多其他资源的启发，我想把采用预训练编码器的U-Net结构进行推广。所以我建立了一个叫动态U-Net的模型。

其思想就是自动为给定的编码器构造解码器。这个编码器可以是之前预训练过的或是你自己定义的。

这个模型是用PyTorch完成的，这里有是对其的分步讲解。

源自：Kerem Turgutlu ——Semantic Segmentation — U-Net