模型预测控制Paolo Falcone 博士面试 (二) - MPC控制的稳定性
第二篇博文推了太久，时间都用来学数据结构和算法，控制专业最大的问题在于很多人只会使用Matlab/Simulink， 不懂数据结构和算法不会写代码，幸亏我认清形式比较早，希望学控制的同学们多写代码，什么时候能用C/C++写出各种数值优化算法的代码才好找工作啊，光懂理论无法C++实现都是扯淡。
言归正传，一般博士面试第二次面试都是考验一下候选人的学术能力。所以第二次面试教授主要是考验我对上个博客中提到的那篇论文的稳定性的理解和评估. 这篇博客主要结合面试来对模型预测控制的稳定性进行一次总结, 纯理论分析对于真实的自动驾驶MPC效果尚未可知。
我们以线性系统作为例子, 假设线性系统的方程为
x + = A x + B u y = C x + D u x^{+} = A x + Bu \\ y = Cx + Du x+=Ax+Buy=Cx+Du
输入量和状态量都存在线性约束
LQR控制一般是针对infinite horizon 的, 优化问题定义如下
J ∞ ( x ) = m i n x , u ∑ i = 0 ∞ x i T Q x i + u i T R u i s . t . x i + 1 = A x i + B u i x 0 = x J^{\infty}(x) = min_{x, u} \sum_{i = 0}^{\infty}x^{T}_{i}Qx_{i} + u_{i}^{T}Ru_{i} \\ s.t. x_{i+1} = Ax_{i} + Bu_{i} \\ x_{0} = x J∞(x)=minx,ui=0∑∞xiTQxi+uiTRuis.t.xi+1=Axi+Buix0=x
MPC优化问题一般定义如下:
J ∗ ( x ) = m i n x , u ∑ i = 0 N − 1 x i T Q x i + u i T R u i s . t . x i + 1 = A x i + B u i x 0 = x C x i + D u i ≤ b J^{*}(x) = min_{x, u} \sum_{i = 0}^{N-1}x^{T}_{i}Qx_{i} + u_{i}^{T}Ru_{i} \\ s.t. x_{i+1} = Ax_{i} + Bu_{i} \\ x_{0} = x \\ Cx_{i} + Du_{i} \leq b J∗(x)=minx,ui=0∑N−1xiTQxi+uiTRuis.t.xi+1=Axi+Buix0=xCxi+Dui≤b
假设 Q = Q T ≥ 0 Q=Q^{T} \geq 0 Q=QT≥0, R = R T ≥ 0 R=R^{T} \geq 0 R=RT≥0
对于线性MPC我们一般都把上述问题转换为二次规划(QP)问题去求解。
然后我盗用一下经典模型预测控制教材 Predictive Control with Constraints里面的Cessana Citation Aircraft的例子
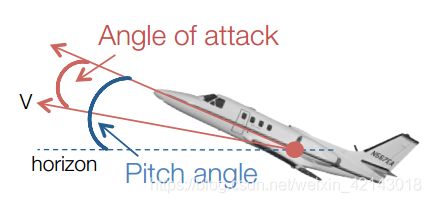
当飞机处于5000m高空，速度为128.2 m/sec的时候，我们可以使用如下的连续的状态方程
x ˙ = [ − 1.2822 0 0.98 0 0 0 1 0 − 5.4292 0 − 1.8366 0 − 128.2 128.2 0 0 ] x + [ − 0.3 0 − 17 0 ] u \dot{x} = \begin{bmatrix} -1.2822&0&0.98&0 \\ 0&0&1&0\\ -5.4292&0&-1.8366&0 \\ -128.2&128.2&0&0 \end{bmatrix} x + \begin{bmatrix} -0.3 \\ 0 \\ -17 \\ 0 \end{bmatrix}u x˙=⎣⎢⎢⎡−1.28220−5.4292−128.2000128.20.981−1.836600000⎦⎥⎥⎤x+⎣⎢⎢⎡−0.30−170⎦⎥⎥⎤u
y = [ 0 1 0 0 0 0 0 1 ] x y = \begin{bmatrix} 0 & 1 &0&0 \\ 0&0&0&1 \end{bmatrix}x y=[00100001]x
该系统的输入量为升降舵偏转角 Input: elevator angle
状态量:
- x 1 x_{1} x1: angle of attack
- x 2 x_{2} x2: pitch angle
- x 3 x_{3} x3: pitch rate
- x 4 x_{4} x4: altitude
输出量:
- pitch angle
- altitude
输入和状态约束:
- elevator angle ± 0.262 \pm0.262 ±0.262 rad( ± 1 5 ∘ \pm15^{\circ} ±15∘)
- elevator rate ± 0.524 r a d ( \pm0.524 rad( ±0.524rad( ± 1 5 ∘ \pm15^{\circ} ±15∘)
- pitch angle ± 0.349 r a d ( \pm0.349 rad( ±0.349rad( ± 3 0 ∘ \pm30^{\circ} ±30∘)
该开环系统是不稳定的
开环极点分别为 0 , 0 , − 1.5594 ± 2.0900 i 0, 0, -1.5594\pm2.0900i 0,0,−1.5594±2.0900i
第一种情况如下图所示：使用LQR控制器， 同时限制输入， t = 0的时候，飞机比期望的高度要高10m, 也就是说初始状态值为 x ( 0 ) = [ 0 ; 0 ; 0 ; 10 ] x(0) = [0;0;0;10] x(0)=[0;0;0;10]. 采样时间 T s = 0.25 s e c T_{s}=0.25 sec Ts=0.25sec, Q = I Q=I Q=I, R = 10 R=10 R=10,
闭环系统是不稳定的，也就是说当我们使用LQR控制器并且限制控制器的输出范围会导致不稳定
第二种情况我们使用MPC控制器同时使用限制输入 ∣ u i ∣ ≤ 0.262 |u_{i}| \leq 0.262 ∣ui∣≤0.262 , 采样时间 T s = 0.25 s e c , T_{s}=0.25sec, Ts=0.25sec,, Q = I Q=I Q=I, R = 10 R=10 R=10, 预测步长 N = 10 N=10 N=10
在设计MPC控制器的时候我们考虑了输入约束，但是没有考虑输入变化率的约束， 最终系统邓等幅震荡(converge to steady state but to a limit cycle)
第三种情况，我们依旧使用MPC控制器, 我们依旧考虑输入约束 ∣ u i ∣ ≤ 0.262 |u_i| \leq 0.262 ∣ui∣≤0.262, 此外我们考虑之前没有考虑输入变化率约束 u ˙ i ≤ 0.349 \dot{u}_i \leq 0.349 u˙i≤0.349, 学成离散形式为 u k − u k − 1 ≤ 0.349 T s u_k - u_{k - 1} \leq 0.349T_s uk−uk−1≤0.349Ts, u − 1 = u p r e v u_{-1} = u_{prev} u−1=uprev, 采样时间 T s = 0.25 s e c T_{s}=0.25sec Ts=0.25sec, Q = I Q=I Q=I, R = 10 R=10 R=10, N = 10 N=10 N=10
我们可以看出来在这种情况下， MPC考虑所有的执行器约束, 闭环系统是稳定的
第四种情况我们改变一下初始值， 初始高度已经提升到100m了，也就是说 x ( 0 ) = [ 0 ; 0 ; 0 ; 100 ] x(0)=[0;0;0;100] x(0)=[0;0;0;100]
在动态过程中Pitch angle出现了巨大的数值，如果我们添加状态约束的话，动态过程中的状态约束很容易不满足
第五种情况 ， 之前我们只考虑了输入约束没有考虑状态约束，下面我们添加状态约束，提高飞机乘客的舒适度 ∣ x 2 ∣ ≤ 0.349 |x_{2}| \leq 0.349 ∣x2∣≤0.349
第六种情况 我们不考虑状态约束，但是我们减少预测步长改为 N = 4 N=4 N=4
我们发现减小预测步长会导致输出不稳定。
这些例子说明了一个道理，标准的MPC是有问题的。
Apollo 里面用的就是Standard MPC， 这样的模型预测控制会有什么样的问题了，控制中有两个重要特性使用这一种MPC是无法保证的
- No feasibility guarantee: MPC问题可能会没有解
- No stability guarantee: 轨迹可能没法收敛到原点
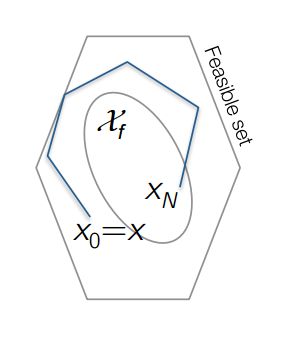
为了证明MPC控制的稳定性, 我们来定义一下Feasible Set
The feasible set X N X_{N} XN is defined as the set of initial states x for which the MPC problem with horizon N N N is feasible, i.e.
X N : = { x ∣ ∃ [ u 0 , … , u N + 1 ] s . t . C u i + D x i ≤ b , i = 1 , … , N } X_{N} := \{ x | \exists [u_{0}, \dots, u_{N + 1}] ~s.t. ~Cu_{i} +Dx_{i} \leq b, i = 1, \dots, N \} XN:={x∣∃[u0,…,uN+1] s.t. Cui+Dxi≤b,i=1,…,N}
就是说对于一些初始状态，我们选择一系列输入，根据系统的状态方程去计算后续状态，其在预测步长内的状态和输入都不会超出我们规定的范围
我们考虑如下的双积分系统
x + = [ 1 1 0 1 ] x + [ 0 1 ] x^{+} = \begin{bmatrix} 1&1\\ 0&1 \end{bmatrix}x + \begin{bmatrix} 0 \\ 1 \end{bmatrix} x+=[1011]x+[01]
状态约束 [ − 5 − 5 ] ≤ x ≤ [ 5 5 ] \begin{bmatrix} -5\\-5 \end{bmatrix} \leq x \leq \begin{bmatrix} 5 \\ 5\end{bmatrix} [−5−5]≤x≤[55]
输入约束 − 0.5 ≤ u ≤ 0.5 -0.5 \leq u \leq 0.5 −0.5≤u≤0.5
预测步长 N = 3 N=3 N=3,
状态惩罚矩阵 Q = [ 1 0 0 1 ] Q = \begin{bmatrix} 1&0 \\ 0 & 1\end{bmatrix} Q=[1001]
输入惩罚系数 R = 10 R=10 R=10
我们使用标准形式的MPC会出现什么情况：
Time step 1 : x ( 0 ) = [ − 4 ; 4 ] , u 0 ∗ ( x ) = 0.5 x(0) = [-4;4], u^{*}_{0}(x) = 0.5 x(0)=[−4;4],u0∗(x)=0.5
Time step 2: x ( 0 ) = [ 0 ; 3 ] , u 0 ∗ ( x ) = − 0.5 x(0) = [0;3], u^{*}_{0}(x) = -0.5 x(0)=[0;3],u0∗(x)=−0.5
Time step 3 : $x(0) = [3;2], MPC优化问题没解啦
我们再来看一个例子, 我们有一个不稳定系统
x + = [ 2 1 0 0.5 ] x + [ 1 0 ] x^{+} = \begin{bmatrix} 2&1\\ 0&0.5 \end{bmatrix}x + \begin{bmatrix} 1\\ 0 \end{bmatrix} x+=[2010.5]x+[10]
状态约束 [ − 10 − 10 ] ≤ x ≤ [ 10 10 ] \begin{bmatrix} -10\\-10 \end{bmatrix} \leq x \leq \begin{bmatrix} 10 \\ 10\end{bmatrix} [−10−10]≤x≤[1010]
输入约束 − 1 ≤ u ≤ 1 -1 \leq u \leq 1 −1≤u≤1
状态惩罚矩阵 Q = [ 1 0 0 1 ] Q = \begin{bmatrix} 1&0 \\ 0 & 1\end{bmatrix} Q=[1001]
下面我们使用不同输入惩罚矩阵 R R R和不同的预测步长 N N N, 求解标准MPC控制问题
(1) R = 10 , N = 2 R=10, N = 2 R=10,N=2
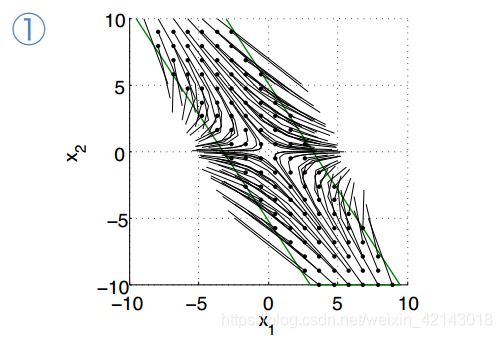(2) R= 2, N = 3
(3) R = 1, N = 4
普通形式的MPC既会导致不稳定又有可能求不到解，那我们怎么办了：
我们改变MPC的优化问题
Introduce terminal cost and constraints to explicitly ensure stability and feasibility:
J ∗ ( x ) = m i n x , u ∑ i = 0 N − 1 x i T Q x i + u i T R u i + x N T P x N s . t . x i + 1 = A x i + B u i x 0 = x C x i + D u i ≤ b x N ∈ X f x 0 = x J^{*}(x) = min_{x, u} \sum_{i = 0}^{N-1}x^{T}_{i}Qx_{i} + u_{i}^{T}Ru_{i} + x_N^TPx_N \\ s.t. x_{i+1} = Ax_{i} + Bu_{i} \\ x_{0} = x \\ Cx_{i} + Du_{i} \leq b \\ x_N \in X_f \\ x_0 = x J∗(x)=minx,ui=0∑N−1xiTQxi+uiTRui+xNTPxNs.t.xi+1=Axi+Buix0=xCxi+Dui≤bxN∈Xfx0=x
其中 x N T P x N x_N^{T}Px_{N} xNTPxN被称为终端代价(Terminal Cost), x N ∈ X f x_N \in X_f xN∈Xf被称为终端约束, 那么问题来了，怎么求 P P P和 X f X_f Xf 才能保证MPC算法是稳定的
待续