MATLAB实现基于模拟退火算法的TSP算法
MATLAB实现的模拟退火算法优化的TSP算法
话不多说,直接上代码(代码主要参考了《matlab智能算法三十个案例分析》,仅供学习交流使用)
matlab
%函数Distance,计算两城市之间的距离
function D = Distanse(a)
%%计算两两城市之间的距离
%输入 a 各城市的位置坐标
%输出 D 两两城市之间的距离
row=size(a,1);
D=zeros(row,row);
for i=1:row
for j=i+1:row
D(i,j)=((a(i,1)-a(j,1))^2+(a(i,2)-a(j,2))^2)^0.5;
D(j,i)=D(i,j);
end
end
函数NewAnswer,解变换生成新解
function S2 = NewAnswer(S1)
%%输入
%S1:当前解
%%输出
%S2:新解
N=length(S1);
S2=S1;
a=round(rand(1,2)*(N-1)+1); %产生两个随机位置用来交换
W=S2(a(1));
S2(a(1))=S2(a(2));
S2(a(2))=W; %得到一个新路线
end
%函数Metropolis,准则函数
function [S,R]=Metropolis(S1,S2,D,T)
%%输入
%S1当前解
%S2新解
%D 距离矩阵
%T 当前温度
%%输出:
%s下一个当前解
%R 下一个当前解的路线距离
R1 = PathLength(D,S1); %计算当前路线长度
N = length(S1); %得到城市个数
R2 = PathLength(D,S2); %计算得到路线长度
dC = R2-R1; %计算能量之差
if dC<0 %如果能量降低,接受新路线
S=S2;
R=R2;
elseif exp(-dC/T)>=rand %以exp(-dC/T)概率接受新路线
S=S2;
R=R2;
else
S=S1;
R=R1;
end
%DrawPath函数,绘制路线
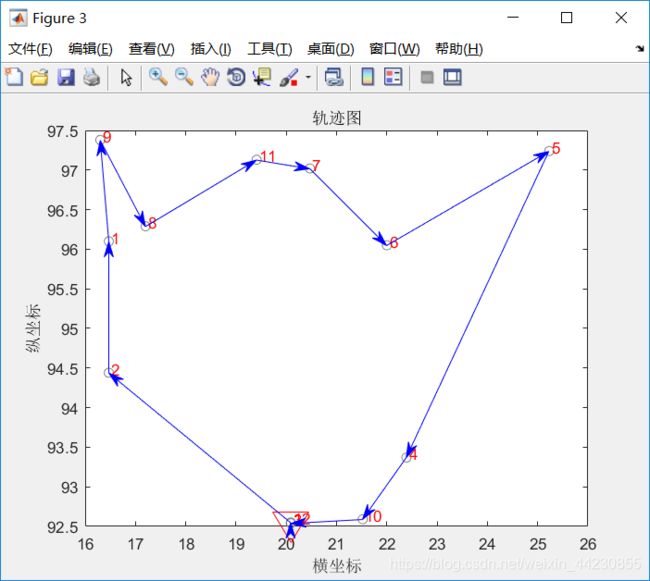
function DrawPath(Chrom,X)
%%画路线图函数
%输入
%Chrom 待画路线
%X 各城市坐标位置
R=[Chrom(1,:) Chrom(1,1)]; %一个随机解(个体)
figure;
hold on
plot(X(:,1),X(:,2),'o','color',[0.5,0.5,0.5])
plot(X(Chrom(1,1),1),X(Chrom(1,1),2),'rv','MarkerSize',20)
for i=1:size(X,1)
text(X(i,1)+0.05,X(i,2)+0.05,num2str(i),'color',[1,0,0]);
end
A=X(R,:);
row=size(A,1);
for i=2:row
[arrowx,arrowy]=dsxy2figxy(gca,A(i-1:i,1),A(i-1:i,2)); %坐标变换
annotation('textarrow',arrowx,arrowy,'HeadWidth',8,'color',[0,0,1]);
end
hold off
xlabel('横坐标')
ylabel('纵坐标')
title('轨迹图')
box on
end
%函数dsxy2figxy,用于坐标变换
function varargout = dsxy2figxy(varargin)
if length(varargin{1}) == 1 && ishandle(varargin{1}) ...
&& strcmp(get(varargin{1},'type'),'axes')
hAx = varargin{1};
varargin = varargin(2:end);
else
hAx = gca;
end
if length(varargin) == 1
pos = varargin{1};
else
[x,y] = deal(varargin{:});
end
axun = get(hAx,'Units');
set(hAx,'Units','normalized');
axpos = get(hAx,'Position');
axlim = axis(hAx);
axwidth = diff(axlim(1:2));
axheight = diff(axlim(3:4));
if exist('x','var')
varargout{1} = (x - axlim(1)) * axpos(3) / axwidth + axpos(1);
varargout{2} = (y - axlim(3)) * axpos(4) / axheight + axpos(2);
else
pos(1) = (pos(1) - axlim(1)) / axwidth * axpos(3) + axpos(1);
pos(2) = (pos(2) - axlim(3)) / axheight * axpos(4) + axpos(2);
pos(3) = pos(3) * axpos(3) / axwidth;
pos(4) = pos(4) * axpos(4 )/ axheight;
varargout{1} = pos;
end
set(hAx,'Units',axun)
%函数OutputPath,输出路径函数
%function p = OutputPath(R)
%%输出路径函数
%输出:R路径
R=[R,R(1)];
N=length(R);
p = num2str(R(1));
for i=2:N
p=[p,'->',num2str(R(i))];
end
disp(p)
%函数PathLength,计算各个路径长度
function len=PathLength(D,Chrom)
%%计算各个个体的路线长度
%输入:
%D 两两城市之间的距离
%Chrom 个体的轨迹
[row,col]=size(D); %得到矩阵D的行数和列数,分别存在变量row,col中
MIND=size(Chrom,1); %将矩阵chrom的行数赋给变量MIND
len=zeros(MIND,1);
for i=1:MIND
p=[Chrom(i,:) Chrom(i,1)];
i1=p(1:end-1);
i2=p(2:end);
len(i,1)=sum(D((i1-1)*col+i2));
end
%下面为主函数:
T0=1000; %初始温度
Tend = 0.001; %终止温度
L=400; %各温度下的迭代次数(链长)
q=0.98; %降温速率
X=[16.4700 96.1000
16.4700 94.4400
20.0900 92.5400
22.3900 93.3700
25.2300 97.2400
22.0000 96.0500
20.4700 97.0200
17.2000 96.2900
16.3000 97.3800
21.5200 92.5900
19.4100 97.1300
20.0900 92.5500];
D=Distance(X); %计算距离矩阵
N=size(D,1); %城市的个数
%%初始解
S1=randperm(N); %随机产生一个初始路线
%画出随机解的路径图
DrawPath(S1,X)
pause(0.0001)
%%输出随机解的路径和总距离
disp('初始种群中的一个随机解:')
OutputPath(S1);
Rlength=PathLength(D,S1);
disp(['总距离:',num2str(Rlength)]);
%%计算迭代的次数Time
Time=ceil(double(solve(['1000*(0.9)^x= ',num2str(Tend)])));
count=0; %迭代计数
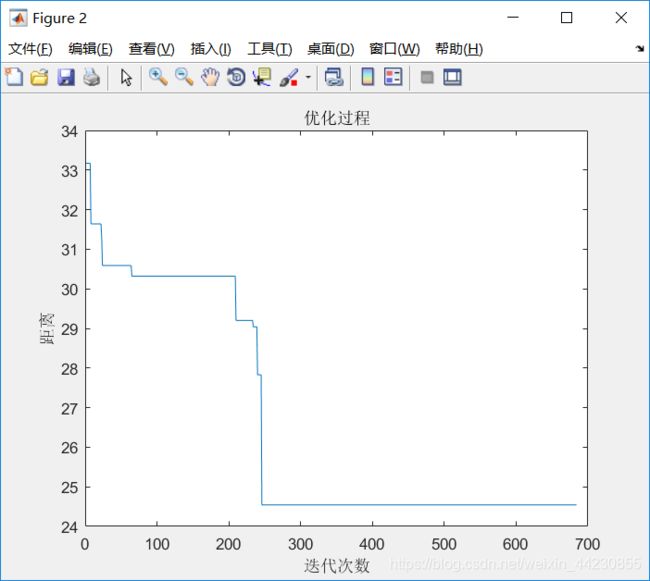
Obj=zeros(Time,1); %目标值矩阵初始化
track=zeros(Time,N); %每代的最优路线矩阵初始化
%%迭代
while T0>Tend
count = count+1;
temp = zeros(L,N+1);
for k=1:L
%%产生新解
S2=NewAnswer(S1);
%%Metropplis法则判断是否接受新解
[S1,R]=Metropolis(S1,S2,D,T0); %Metropolis抽样算法
temp(k,:) = [S1 R]; %记录下一路线及其路程
end
%%记录每次迭代过程的最优路线
[d0,index]=min(temp(:,end)); %找出当前温度下最优路线
if count==1||d0