【信号与系统学习笔记】—— 连续时间非周期信号的傅里叶变换

一、傅里叶正变换、逆变换

在之前的 $Blog$ 里面，我们都已经进行过了推导。我们这里再一次简洁地推一下下：
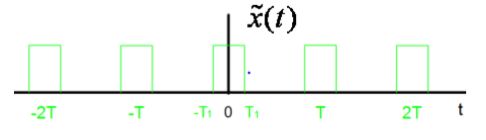
对于下面这样的周期矩形信号，我们可以有下面的结论：

$$a_k=\frac{1}{T}{\int }_{-T_1}^{+T_1}x(t)e^{-jk{\omega }_{0}t}dt\text{\hspace{1em}(1)}$$

下面我们考虑这样一个非周期信号：

我们发现，其实在区间 $-T_1$ ~ $T_1$ 内，有：$x(t)=x(t)$。那么我们把这个式子带入（1）得到：$$\begin{array}{rl}& a_k=\frac{1}{T}{\int }_{-T_1}^{+T_1}x(t)e^{-jk{\omega }_{0}t}dt\\ & T{a}_k={\int }_{-T_1}^{+T_1}x(t)e^{-jk{\omega }_{0}t}dt\end{array}$$
我们发现，现在的式子就变成针对 $x(t)$ 的了，那么对于 $x(t)$ ，他不是只在 区间 $-T_1$ ~ $T_1$ 内才有值嘛，那么其实在区间 $-T_1$ ~ $T_1$ 内积分就可以等价于在 $-\infty$ ~ $+\infty$ 内积分了：$$T{a}_k={\int }_{-\infty }^{+\infty }x(t)e^{-jk{\omega }_{0}t}dt$$
当 $T$ 趋近于无穷时，谱线的间隔趋于0，那么 $k{\omega }_0$（本来代表的就是一根一根的谱线的横坐标，因为现在谱线间隔没有了，所以这个 $k{\omega }_0$ 就可以用一个连续的 $\omega$ 来表示了：$$X(j\omega )={\int }_{-\infty }^{+\infty }x(t)e^{-j\omega t}dt$$

傅里叶逆变换的推导思路也很清晰：

还记得我们在上一篇 $Blog$ 里面说过的吗？连续时间周期矩形信号的频谱可以看成是对连续时间非周期矩形信号频谱的采样。 所以我们有下面的式子：$$a_k=\frac{1}{T}X(jk{\omega }_0)$$
下面我们依然考虑一个连续时间周期矩形信号的傅里叶级数表示：$$\begin{array}{rl}x(t)& =\sum _{k=-\infty }^{+\infty }{a}_k{e}^{jk{\omega }_{0}t}\\ & =\sum _{k=-\infty }^{+\infty }\frac{1}{T}X(jk{\omega }_0)e^{jk{\omega }_{0}t}\\ & =\frac{1}{2\pi }\sum _{k=-\infty }^{+\infty }X(jk{\omega }_0)e^{jk{\omega }_{0}t}{\omega }_0\end{array}$$
当 $T$ 趋于无穷时，我们用求和去极限的方式表示（就引入了积分）：
$$\begin{array}{rl}x(t)=\underset{T\to \infty }{\lim }x(t)& =\underset{T\to \infty }{\lim }\frac{1}{2\pi }\sum _{k=-\infty }^{+\infty }X(jk{\omega }_0)e^{jk{\omega }_{0}t}{\omega }_0\\ & =\frac{1}{2\pi }\underset{T\to \infty }{\lim }\sum _{k=-\infty }^{+\infty }X(jk{\omega }_0)e^{jk{\omega }_{0}t}{\omega }_0\\ & =\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }X(j\omega )e^{j\omega t}d\omega \end{array}$$
因此，我们就推出了傅里叶逆变换公式。

下面，我们把傅里叶正变换和逆变换写到一起方便记忆：$$X(j\omega )={\int }_{-\infty }^{+\infty }x(t)e^{-j\omega t}dt$$
$$x(t)=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }X(j\omega )e^{j\omega t}d\omega$$

1.1 能够进行傅里叶变换的条件

有两个条件：满足其中之一即可：
【1】信号的能量有限：$${\int }_{-\infty }^{+\infty }|x(t){|}^{2}dt<\infty$$
【2】信号绝对可积：$${\int }_{-\infty }^{+\infty }|x(t)|dt<\infty$$

1.2 连续时间的周期信号频谱和非周期信号频谱的关系

连续时间周期信号的频谱是其对应的非周期信号频谱的样本。（注：这个“对应的” 应该怎么解释呢？因为任何一个周期信号都可以是其一个周期的信号做周期延拓得来的）

非周期信号的频谱就是其对应的周期信号频谱的包络

1.3 几种常见信号的傅里叶变换（记忆）

在记录之前，我们打算说明一下广义采样函数的定义。我们之前的 $sinc$ 函数是狭义的采样函数，那么为了和老师授课所用的符号一致，我们以后在某些场合将采用广义的采样函数 $Sa$ 函数，其函数表达式为：$$Sa(x)=\frac{sin(x)}{x}$$
当 $x=k\pi (k=\pm 1,\pm 2,\cdots )$时，$Sa(x)=0$

对于狭义的 $sinc(x)$ 函数，当 $x=\pm k$（$k$ 为正整数时），$sinc(x)=0$

1.3.1 非周期矩形信号的频谱：

对于非周期矩形信号的频谱，大家可以按照我以前那个 $Blog$ 里面的方法记忆（更容易记忆一些）：
若这个非周期矩形信号的脉冲宽度是 $\tau$，那么其频谱函数就是：$\tau sinc(\tau f)$

我们看看下面的例子：

你看，脉冲宽度是 $2T_1$，那么频谱直接出来啦，就是：$2T_{1}sinc(2T_{1}f)$，你想把它写成 $\omega$ 的表达式也很方便，就是：$2T_{1}sinc(2T_1\frac{\omega }{2\pi })=2T_{1}sinc(T_1\frac{\omega }{\pi })$
根据狭义采样函数的定义，在：$$sinc=0(if{T}_1\frac{\omega }{\pi }=\pm 1,\pm 2,\cdots )$$
我们可以得到频谱的第一个零点的坐标就是：$\omega =\frac{\pi }{T_1}$

1.3.2 频谱是非周期矩形波的信号

如果给出的是一个矩形的频谱，要你求原时域函数呢？如下图：

我们先直接用公式求解：$$\begin{array}{rl}x(t)& =\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }X(j\omega )e^{j\omega t}d\omega \\ & =\frac{1}{2\pi }{\int }_{-\omega }^{+\omega }{e}^{j\omega t}d\omega \\ & =\frac{sin(\omega t)}{\pi t}\\ & =\frac{\omega }{\pi }\frac{sin(\omega t)}{\omega t}=\frac{\omega }{\pi }Sa(\omega t)\end{array}$$
对于 Sa(x) 函数而言，我们之前也提到过了，当 $x=k\pi (k=\pm 1,\pm 2,\cdots )$时，$Sa(x)=0$
所以，$x(t)$ 在正半时间轴的第一个零点就是：$x=\frac{\pi }{\omega }$

1.3.3 单位冲激信号的傅里叶变换

这个结论我们直接记忆：单位冲激信号的傅里叶变换是幅度为 1 的频谱：

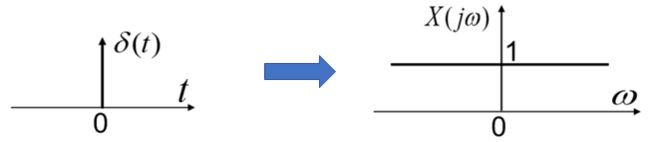
大家看分析一下：单位冲激信号的频谱居然包括了所有频率范围，并且各个频率成分的幅度都是 1 ！相位也相同！ 这也是为什么 $\delta$ 信号在这门课如此重要的原因！

1.3.4 频谱是单位冲激的信号

如果某一个信号的频谱是单位冲激，那么做一下傅里叶逆变换：$$\begin{array}{rl}x(t)& =\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }\delta (j\omega )e^{j\omega t}d\omega \\ & =\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }\delta (j\omega )e^{0}d\omega \\ & =\frac{1}{2\pi }\end{array}$$
【注：上面推导的第二行用了单位冲击信号的采样性】

由此可见，幅度为 $\frac{1}{2\pi }$ 的直流信号的频谱是单位冲激

1.3.5 单边指数信号的傅里叶变换

$$x(t)=e^{-at}u(t)(a>0)$$
其频谱就是：$$X(j\omega )=\frac{1}{a+j\omega }$$

---