用python手写KNN算法+kd树及其BBF优化(原理与实现)(上篇)
用python手写KNN算法+kd树及其BBF优化(原理与实现)(上篇)
初学python和机器学习,突然兴起想动手用python实践一下KNN算法,本来想着这个算法原理很简单明了,应该实现起来没什么大问题,然而真正上手的时候问题频出,花了好一些功夫挨个排除各种奇怪的bug,总算是大功告成。接下来我会介绍一下算法的手写实现和在此过程中亲遇的各种问题,希望能够帮到大家。实验所需数据链接在文章最后。
ps:从学习C语言以来形成了print调试的毛病,所以在代码中保留了一些用于调试的输出重要信息的print语句,放在了后面的完整print信息版代码中,方便理解代码和调试。千万注意在使用time()方法测试程序运行时间时要把这些调试的print语句注释掉。
pps:关于numpy的疑惑建议随时参考https://www.runoob.com/numpy/numpy-dtype.html,很方便
1. KNN算法与kd树简介
1.1 什么是KNN算法?
网上关于KNN的详细介绍很多,简单来说,KNN是一种有监督分类算法,通过计算待分类数据点,与已有数据集中的所有数据点的距离。取距离最小的前K个点,根据“少数服从多数“的原则,将这个数据点划分为出现次数最多的那个类别。如图由KNN得到Xu属于ω1
因此,将分类点输入的过程就是KNN算法的学习过程,将已分类点全部输入后,要完成对未分类点所属类别的预测,重点是找出距离未分类点最近的前K个已分类点
1.2 为什么需要kd树?
前面我们说道,要完成对未分类点所属类别的预测,重点是找出距离未分类点最近的前K个已分类点。那么,对于每个未分类点,一般我们需要求出它与所有以分类点的距离,然后找出前k个距离最小的已分类点。如果已分类点集合中有n个点,那么如果我们要对m个未分类点进行预测,时间复杂度为O(m*n)。当n很大时,我们认为这样不是很高效。
那么,有没有一种方法让上述复杂度变为O(mlogn)呢?这时我们想到了二叉树。类比二叉查找树(BST),Kd-Tree即K-dimensional tree,是一棵二叉树,树中存储的是一些K维数据。在一个K维数据集合上构建一棵Kd-Tree代表了对该K维数据集合构成的K维空间的一个划分。即树中的每一个结点就相应了一个K维的超矩形区域(Hyperrectangle),kd树的详细介绍以及如何构造kd树将在下面介绍。
2. 数据集准备
首先,准备数据集:这里的数据集即指KNN算法的训练集和测试集。对于KNN算法来说,将训练集输入的过程就是KNN算法学习的过程。训练集和测试集由多个样本构成,每个样本由其特征向量和标签构成,也就是由特征和类别构成。举个例子,某样本的特征向量为(唱,跳,rap,篮球),标签为蔡徐坤,将它作为训练集输入后,测试集中我们给出(唱,跳,rap,鸡你太美),由KNN算法我们预测出该测试样本对应标签为蔡徐坤,和测试标签对比发现本次预测成功。为了方便编程,我们将训练集和测试集处理均处理为由(特征1,特征2,… ,特征n,标签)这样的向量组成的集合,称之为数据矩阵。如:
训练集(或测试集):
唱,跳,rap,篮球,蔡徐坤
拐,黑土,不差钱,小品,赵本山
…
为了简单这次实验用的是DBRHD数据集。
2.1 DBRHD数据集
DBRHD(Pen-Based Recognition of Handwritten Digits Data Set)是UCI的机器学习中心提供的数字手写体数据库可以在https://archive.ics.uci.edu/ml/datasets/PenBased+Recognition+of+Handwritten+Digits下载,不过我相信从这里得到的数据集会让你一头雾水,所以我会把我用到的数据文本放到文章后面的链接中。
DBRHD数据集包含大量的数字0~9的手写体图片,这些图片来源于44位不同的人的手 写数字,图片已归一化为以手写数字为中心的32*32规格的图片。DBRHD的训练集与测试集组成如下:
(1)训练集:7,494个手写体图片及对应标签,来源于40位手写者
(2)测试集:3,498个手写体图片及对应标签,来源于14位手写者
我们把训练集和测试集转化为前面介绍的向量集合的格式存放到文本中,分为两个版本:
(1)特征个数为16的版本:
训练集training1.txt:

其中每一行代表一个(特征1,特征2,…,特征16,标签)的向量,
如47,100,27,81,57,37,26,0,0,23,56,53,100,90,40,98这16个特征决定了它代表数字8。下面的测试集也是类似。
测试集test1.txt:

(2)特征个数为1024的版本(这一版训练集样本有1934个,测试集样本有946个):
训练集training2.txt和测试集test2.txt
(太占版面了,只贴一个向量吧,前面1024个0或1组成的特征代表数字8)

2.2 编写数据读取函数
先导入这次实验需要的全部模块
import numpy as np
import queue # 后续bbf会用
import time
读取文件函数:
def loadData(filePath): # 读文件
with open(filePath, 'r+') as fr:
# with语句会自动调用close()方法,且比显式调用更安全
lines = fr.readlines()
data = []
for line in lines: # 逐行读入
items = line.strip().split(",")
data.append([int(items[i]) for i in range(len(items))])
return np.asarray(data) # 以np.ndarray类型数组返回
3. 构建kd树(kd-tree)
得到数据后我们就可以构建kd树了,KNN算法其实本身并没有真正意义的学习的过程,构建kd树的过程就作为它的“学习”过程。
首先,我们要知道什么是kd树:
我们先回想一下二叉查找树(或二叉排序树)即BST:
二叉查找树(Binary Search Tree,BST)。是具有例如以下性质的二叉树:
1)若它的左子树不为空。则左子树上全部结点的值均小于它的根结点的值;
2)若它的右子树不为空,则右子树上全部结点的值均大于它的根结点的值;
3)它的左、右子树也分别为二叉排序树;
我们要在BST中查找一个数,仅仅须要将查询数据与结点值进行比较然后选择相应的子树继续往下查找就可以,查找的平均时间复杂度为O(logN)。
不难看出BST仅适用于一维的数据集合
能否用某种方法将这种数据集合切割(BST是直接按数字大小左右分割)的思想用到K维的数据集合呢?答案就是kd树。
这时我们会遇到几个问题:
3.1 如何划分K维空间
一维数据可以直接比大小确定左右分支,而对于一个K维数据集(K>=1),如何确定其左右分支呢?
答案也是比大小,不过在比较之前要指定一个维度,如(2,3)与(5,1)比较,在维度0上,2<5,所以(2,3)<(5,1),在维度1上,3>1,所以(2,3)>(5,1)。每次选择一个维度Di来对K维数据进行划分,相当于用一个垂直于该维度Di的超平面将K维数据空间一分为二。平面一边的全部K维数据在Di维度上的值小于平面另一边的全部K维数据相应维度上的值。
这样,我们每选择一个维度进行如上的划分,就会将K维数据空间划分为两个部分。我们继续分别对这两个子K维空间进行如上的划分。又会得到新的子空间,对新的子空间又继续划分,反复以上过程直到每一个子空间达到一个理想的大小或者不能继续划分。
这时我们应当意识到,以上就是构造kd-tree的过程。
3.2 如何确定在哪个维度上划分
上述过程中我们需要知道,每次对子空间的划分时,应当选择哪个维度。
为了使每次的切割效果最好,我们应当选择各向量在该维度上的值方差最大的那个维度。举个例子,某三维向量集合{(1,2,3),(100,3,4),(50,3,2),(150,3,3),(200,2,4)},我们发现1,100,50, 150,200的方差是最大的,所以本次在维度0上划分集合效果最好。每次划分中,我们均选择一个方差最大的维度进行划分。
3.3 确定维度后,怎样确定划分值
在某个维度上进行划分时,如何确保在这一维度上的划分得到的两个子集合的数量尽量相等。即左子树和右子树中的结点个数尽量相等呢?显然,选择中位数作为划分值是最合理的,还是上面的例子,对于三维向量集合
{(1,2,3),(100,3,4),(50,3,2),(150,3,3),(200,2,4)},我们已经确定在维度0上划分,故选择1,100,50,150,200的中位数150作为划分值
ps:numpy中求1,2,3,4,5,6的中位数会得到3.5
3.4 划分到何种程度就不再划分
我在实践中发现,划分到每个集合只剩一个元素,往往不能让算法达到最好的效果,所以我设置了一个阈值,即最小划分个数threshold ,元素个数低于此值就无需划分。
3.5 一个容易bug的坑点
这是实现过程中遇到的一个坑点。思考一个问题,在写判断语句时,我们应当让小于划分值的向量归入左子树集合(方案一),还是让小于等于划分值的向量归入左子树(方案二)?这似乎不是一个值得讨论的问题,但是我们举两个例子:
(1)假设当前向量集合在维度Di上方差最大,各向量在维度Di上的值为1,1,1,2,2,显然其中位数是1,如果我们选择方案一,那么划分得到的左子树为空,该集合全部向量归入右子树,接下来再对右子树的向量集合进行划分时,我们还是会得到维度Di上方差最大,还是遇到和前面一样的情况,将全部向量归入右子树,这在递归建树的过程中意味着死循环。
(2)再假设当前向量集合在维度Di上方差最大,各向量在维度Di上的值为1,1,2,2,2,显然其中位数是2,如果我们选择方案二,那么划分得到的右子树为空,该集合全部向量归入左子树,接下来再对左子树的向量集合进行划分时,我们还是会得到维度Di上方差最大,还是遇到和前面一样的情况,将全部向量归入左子树,同样形成死循环。
我们发现,不论选择方案一还是方案二,都会遇到问题,解决方案是:
对于各向量在维度Di上的值的集合,我们不仅要得到其中位数,还要得到其最小值和最大值,如果中位数 != 最小值,选择方案一,否则,若中位数 != 最大值,选择方案二。如果中位数 , 最小值 ,最大值三者相等,则其方差为0,此维度不会作为划分维度。
3.6 kd树图示
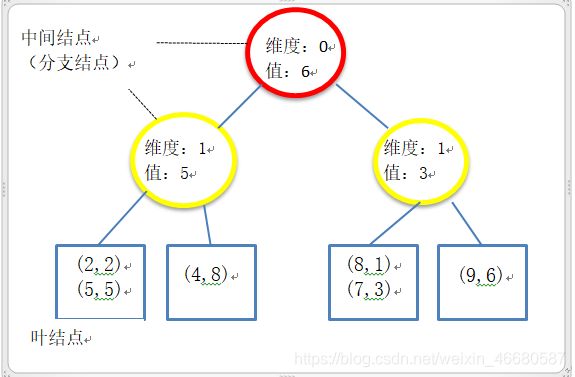
ps:我采用的kd-tree结构是数据仅仅存放在叶子结点,而根结点和中间结点存放一些空间划分信息(如划分维度、划分值),以二维数据集合(2,2), (5,5), (9,6), (4,8), (8,1), (7,3)为例,其划分与kd树如图。网上还有其他kd-tree版本,这里不赘述。
3.7 kd-tree构建的代码实现
明白了上述问题后就可以建树了。
先定义分支结点(中间结点)
class kdNode():
# 分支结点
def __init__(self, demo, value, left, right):
# 切割维度,切割值,左子树,右子树
self.demo = demo
self.value = value
self.left = left
self.right = right
kd-tree及其构建:
class kdtree():
# kd树
"""
构建kd-tree,data_array为初始的数据集合,数据类型是np.ndarray,
threshold是最小划分个数
"""
def __init__(self, data_array, threshold):
self.threshold = threshold # 最小分支阈值,数据个数低于此值不在划分
row, col = data_array.shape
k = col - 1 # k指维度,即特征向量的元素个数
"""寻找方差最小的维度"""
def getMaxDimension(data): # data即当前待划分的数据集合
maxv = -1 # 记录当前最大方差
maxi = -1 # 记录当前方差最大的维度
for i in range(k):
a = np.var(data[:, i]) # 计算维度i对应的方差
if a > maxv:
maxi = i
maxv = a
return maxi, maxv # 返回最大方差对应的维度和最大方差值
"""
创建一个分支结点
"""
def createNode(data):
split_dimension, maxv = getMaxDimension(data)
# split_dimension, maxv分别指划分轴(维度)和最大方差值
if maxv == 0:
# 考虑边界情况,最大方差为0时当前数据不必划分,直接作为叶子结点
return data
split_value = np.median(data[:, split_dimension])
# 取当前维度下的中位数作为划分值
maxvalue = np.max(data[:, split_dimension]) # 当前维度下的最大元素
minvalue = np.min(data[:, split_dimension]) # 当前维度下的最小元素
left = [] # 保存在split_dimension下小于(或等于)split_value的点
right = [] # 保存在split_dimension下大于(或等于)split_value的点
for i in range(len(data)):
if split_value < maxvalue: # 避免0,0,0,1,2这样的分不开
if data[i][split_dimension] <= split_value:
left.append(list(data[i]))
else:
right.append(list(data[i]))
elif split_value > minvalue: # 避免0,1,2,2,2这样的分不开
if data[i][split_dimension] < split_value:
left.append(list(data[i]))
else:
right.append(list(data[i]))
# 最小分支阈值,低于此值不再划分
root = kdNode(split_dimension, split_value,
(createNode(np.asarray(left)) if len(left) >= threshold else np.asarray(left)),
(createNode(np.asarray(right)) if len(right) >= threshold else np.asarray(right)))
# 递归建树,注意当点集中元素个数小于最小分支阈值时直接作为叶结点而不必分支
return root
self.root = createNode(data_array)
4. 利用kd树进行最近邻和K近邻查找
构建好kd树后,我们就可以利用它为给定点寻找K近邻,再此之前,我们先搞明白如何利用kd树寻找最近邻。(最近邻即距离最近的点,K近邻即前K个距离最近的点。)
4.1 利用kd树寻找最近邻
给定一棵用训练点集构造的kd树,再给定一个待查询点Q,寻找距离Q最近的训练点。(这里的一个点指的是一个特征向量)
(1)将查询数据Q从kd-treede 根结点开始,依照Q与各个结点的比较结果向下访问kd-tree,直至达到叶子结点。其中Q与结点的比较指的是将Q相应于结点中的k维度上的值与m进行比较,小于则访问左子树,否则右子树。
记录当前最近邻点和最小距离(记为minDis)。
(2)进行回溯操作,该操作是为了找到离Q更近的最近邻点”,即推断未被访问过的分支里是否还有离Q更近的点。它们之间的距离小于minDis。回溯是必要的,任意上面的二维数据图示为例:
给定一点(7,4),查询kd树会找到(9,6),而最近的点应该是
(7,3)

回溯的推断过程是从下往上进行的递归过程,不断回到(1)步骤直到回溯到根结点时已经不存在与P更近的分支。
那么,如何推断未被访问过的树分支里是否还有离Q更近的点?
从几何空间上来看,就是推断以Q为中心,以mindis为半径的超球面与树分支Branch代表的超矩形之间是否相交。看起来有点复杂,其实非常简单,把分支结点的两个值记为Di(划分维度)和Dv(划分值)Q在划分维度上的值为Q[Di],只需判断|Q[Di]-Dv| 在上述寻找最近邻的基础上,我们维护一个大小为K的列表klist,其中存放目前找到的前K个最近点,klist的最后一个元素始终是这K个点中距离最远的(记为klist[k-1]),这个最远距离记为kDis,回溯时,判断|Q[Di]-Dv| 寻找K近邻的代码如下: 由上述代码得到一个给定点的k近邻后,我们所作的就是选出k近邻对应标签出现次数最多的那个,作为给定点的预测标签。 KNN预测代码如下: 接下来是main函数: 对比不使用kd树的情况(将knn()中将最小划分个数设为较大值如10000即可) 可以看到,虽然建kd树花费了一定的时间,但是预测用时明显比不使用kd树缩短了很多。 上面的代码删掉了我的在敲代码的时候的各种print调试信息,但是那些我感觉还是挺有用的,沉迷print调试的同鞋应该会懂吧~ 注意上面我们使用的是training1.txt和test1.txt两个文本提供的数据集 本次实验所需数据集:4.2 利用kd树寻找K近邻
ps2:n维向量的距离计算公式:

ps3: 尽量使用numpy提供的内置函数进行向量运算(如求距离时),其速度要比自己写for循环快的多的多。"""寻找vec对应的k邻近,klist为(距离,[向量])构成的列表,存放vec的k个近邻点的信息,初始为空"""
def findn(root, vec, klist, k):
if type(root) == np.ndarray: #到达叶结点
if len(root) == 0:
return
temp = (root[:, :-1] - vec) ** 2
for i in range(len(temp)):
a = sum(temp[i])
if len(klist) != k:
klist.append((a, root[i]))
klist.sort(key=lambda x: x[0]) # 按距离排序
else:
if a < klist[k - 1][0]:
klist[k - 1] = [a, root[i]]
klist.sort(key=lambda x: x[0]) # 按距离排序
else:
if vec[root.demo] < root.value:
findn(root.left, vec, klist, k)
if abs((vec[root.demo] - root.value)**2) < klist[len(klist) - 1][0]:
findn(root.right, vec, klist, k) # 回溯
else:
findn(root.right, vec, klist, k)
if abs((vec[root.demo] - root.value)**2) < klist[len(klist) - 1][0]:
findn(root.left, vec, klist, k) # 回溯
5. 利用kd树完成KNN预测
如,假设K=3,我们得到的3个距离最近的点的标签分别为蔡徐坤,蔡徐坤,郭宝坤,那么最终预测结果就应该是蔡徐坤。
这里有一个坑点,就是当标签为蔡徐坤(dis = 3),郭宝坤(dis = 5),陈坤(dis=10)时,我们无法投票选出出现最多的那个标签,这个时候一定要选距离给定点距离最近的那个标签作为预测标签,即蔡徐坤。"""
选出列表中出现次数最多的元素,一个需要注意的问题是像[2,2,1,1,3]这样的怎么选,因为之前已经按距离从小到大排序,所以应选2
"""
def findMain(alist):
hashtable = [0 for i in range(10)]
for i in range(len(alist)):
hashtable[alist[i]]+=1
maxnum = -1
main = -1
for i in range(len(alist)):
if hashtable[alist[i]]>maxnum:
main = alist[i]
maxnum = hashtable[alist[i]]
return main
"""预测给定点的标签"""
def forecast(root, data, k):
a = [] #作为findn方法中的klist参数
findn(root, data, a, k)
L = len(a[0][1]) #其实就是向量维度
res = []
for i in range(len(a)):
res.append(a[i][1][L - 1])
return findMain(res)
"""用train_list建树,用KNN对test_list中的向量进行预测并输出正确率"""
def knn(train_list, test_list, k):
tic1 = time.time()
root = kdtree(train_list, 10).root #最小划分次数设为10
print("最小划分个数: 10")
print("k = "+str(k))
tic2 = time.time()
num = 0
for i in range(len(test_list)):
a = forecast(root, np.asarray(test_list[i][:-1]), k)
if a == test_list[i][-1]:
num += 1
print("正确率:"+str(num / len(test_list))) # 预测准确率
toc = time.time()
print("总用时:" + str(1000*(toc-tic1))+"ms")
print("训练用时:" + str(1000*(tic2-tic1))+"ms")
print("预测用时:" + str(1000*(toc-tic2))+"ms")
if __name__ == "__main__":
train_list = loadData("training1.txt")
test_list = loadData("test1.txt")
knn(train_list, test_list, 3) # K值设为3
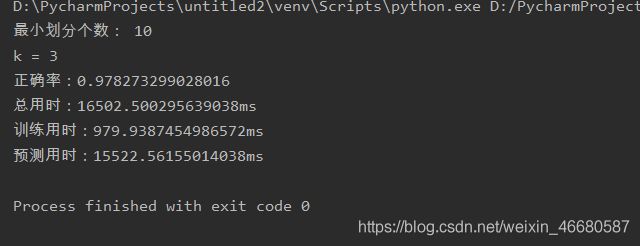
6. 运行结果与效果对比
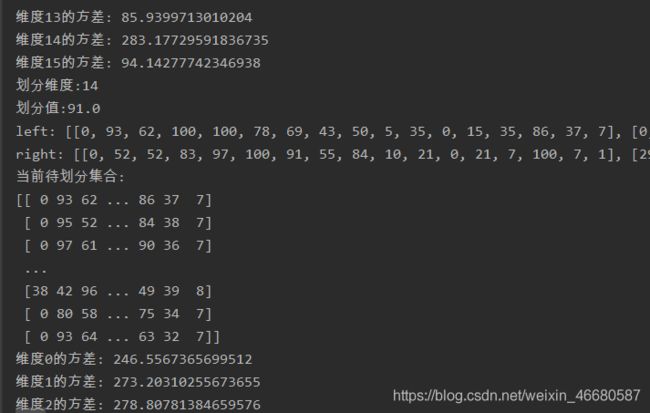
7. 完整print信息版代码
这里是保留print信息的版本import numpy as np
def loadData(filePath): # 读文件
with open(filePath, 'r+') as fr:
# with语句会自动调用close()方法,且比显式调用更安全
lines = fr.readlines()
data = []
for line in lines: # 逐行读入
items = line.strip().split(",")
data.append([int(items[i]) for i in range(len(items))])
return np.asarray(data) # 以np.ndarray类型数组返回
class kdNode():
# 分支结点
def __init__(self, demo, value, left, right):
# 切割维度,切割值,左子树,右子树
self.demo = demo
self.value = value
self.left = left
self.right = right
class kdtree():
# kd树
"""
构建kd-tree,data_array为初始的数据集合,数据类型是np.ndarray,
threshold是最小划分个数
"""
def __init__(self, data_array, threshold):
self.threshold = threshold # 最小分支阈值,数据个数低于此值不在划分
row, col = data_array.shape
k = col - 1 # k指维度,即特征向量的元素个数
"""寻找方差最小的维度"""
def getMaxDimension(data): # data即当前待划分的数据集合
print("当前待划分集合: ") # 输出待分割的数据集合
print(data)
maxv = -1 # 记录当前最大方差
maxi = -1 # 记录当前方差最大的维度
for i in range(k):
a = np.var(data[:, i]) # 计算维度i对应的方差
print("维度" + str(i) + "的方差" + ": " + str(a)) # 输出每个维度的方差
if a > maxv:
maxi = i
maxv = a
return maxi, maxv # 返回最大方差对应的维度和最大方差值
"""
创建一个分支结点
"""
def createNode(data):
split_dimension, maxv = getMaxDimension(data)
# split_dimension, maxv分别指划分轴(维度)和最大方差值
print("划分维度:" + str(split_dimension)) # 输出划分维度
if maxv == 0:
# 考虑边界情况,最大方差为0时当前数据不必划分,直接作为叶子结点
return data
split_value = np.median(data[:, split_dimension])
# 取当前维度下的中位数作为划分值
print("划分值:" + str(split_value)) #输出划分值
maxvalue = np.max(data[:, split_dimension]) # 当前维度下的最大元素
minvalue = np.min(data[:, split_dimension]) # 当前维度下的最小元素
left = [] # 保存在split_dimension下小于(或等于)split_value的点
right = [] # 保存在split_dimension下大于(或等于)split_value的点
for i in range(len(data)):
if split_value < maxvalue: # 避免0,0,0,1,2这样的分不开
if data[i][split_dimension] <= split_value:
left.append(list(data[i]))
else:
right.append(list(data[i]))
elif split_value > minvalue: # 避免0,1,2,2,2这样的分不开
if data[i][split_dimension] < split_value:
left.append(list(data[i]))
else:
right.append(list(data[i]))
print("left: ", end="") #输出左右分支集合
print(left)
print("right: ", end="")
print(right)
# 最小分支阈值,低于此值不再划分
root = kdNode(split_dimension, split_value,
(createNode(np.asarray(left)) if len(left) >= threshold else np.asarray(left)),
(createNode(np.asarray(right)) if len(right) >= threshold else np.asarray(right)))
# 递归建树,注意当点集中元素个数小于最小分支阈值时直接作为叶结点而不必分支
return root
self.root = createNode(data_array)
n = 0
"""寻找vec对应的k邻近,klist为(距离,[向量])构成的列表,存放vec的k个近邻点的信息,初始为空"""
def findn(root, vec, klist, k):
if type(root) == np.ndarray: #到达叶结点
if len(root) == 0:
return
temp = (root[:, :-1] - vec) ** 2
for i in range(len(temp)):
a = sum(temp[i])
global n
n += 1
if len(klist) != k:
klist.append((a, root[i]))
klist.sort(key=lambda x: x[0]) # 按距离排序
else:
if a < klist[k - 1][0]:
klist[k - 1] = [a, root[i]]
klist.sort(key=lambda x: x[0]) # 按距离排序
else:
if vec[root.demo] < root.value:
findn(root.left, vec, klist, k)
if abs((vec[root.demo] - root.value)**2) < klist[len(klist) - 1][0]:
findn(root.right, vec, klist, k) # 回溯
else:
findn(root.right, vec, klist, k)
if abs((vec[root.demo] - root.value)**2) < klist[len(klist) - 1][0]:
findn(root.left, vec, klist, k) # 回溯
"""
选出列表中出现次数最多的元素,一个需要注意的问题是像[2,2,1,1,3]这样的怎么选,因为之前已经按距离从小到大排序,所以应选2
"""
def findMain(alist):
hashtable = [0 for i in range(10)]
for i in range(len(alist)):
hashtable[alist[i]]+=1
maxnum = -1
main = -1
for i in range(len(alist)):
if hashtable[alist[i]]>maxnum:
main = alist[i]
maxnum = hashtable[alist[i]]
print("预测标签:"+str(main))
return main
"""预测给定点的标签"""
def forecast(root, data, k):
a = [] #作为findn方法中的klist参数
global n
n = 0
findn(root, data, a, k)
print("遍历了" + str(n) + "个点")
L = len(a[0][1]) #其实就是向量维度
res = []
for i in range(len(a)):
res.append(a[i][1][L - 1])
print("K邻近标签:", end="")
print(res)
return findMain(res)
"""用train_list建树,用KNN对test_list中的向量进行预测并输出正确率"""
def knn(train_list, test_list, k):
root = kdtree(train_list, 10).root #最小划分次数设为10
print("最小划分个数: 10000")
print("k = "+str(k))
num = 0
for i in range(len(test_list)):
a = forecast(root, np.asarray(test_list[i][:-1]), k)
if a == test_list[i][-1]:
num += 1
print("正确率:"+str(num / len(test_list))) # 预测准确率
if __name__ == "__main__":
train_list = loadData("pendigits.tra")
test_list = loadData("pendigits.tes")
knn(train_list, test_list, 3) # K值设为3
8. 一个明显的问题
它们的特征向量是16维,然而当我们使用training2.txt和test2.txt两个文本提供的数据集(特征向量是1024维)时,会发现,耗时很长且使用kd树与不使用kd树在时间上并没有什么差距。这就要引出后面的BBF优化了。用python手写KNN算法+kd树及其BBF优化(原理与实现)(下篇)9.附录
链接:https://pan.baidu.com/s/1qJ1_uGjYVTR7kegwpQW19Q
提取码:30kt
复制这段内容后打开百度网盘手机App,操作更方便哦