IMDB影评文本分类
IMDB 数据集
TensorFlow 中包含 IMDB 数据集。我们已对该数据集进行了预处理,将影评(字词序列)转换为整数序列,其中每个整数表示字典中的一个特定字词。
以下代码会将 IMDB 数据集下载到您的计算机上(如果您已下载该数据集,则会使用缓存副本):
import tensorflow as tf
from tensorflow import keras
from keras.datasets import imdb
(train_data,train_labels),(test_data,test_labels) = imdb.load_data(num_words=10000)
参数 num_words=10000 会保留训练数据中出现频次在前 10000 位的字词。为确保数据规模处于可管理的水平,罕见字词将被舍弃
该数据集已经过预处理:每个样本都是一个整数数组,表示影评中的字词。每个标签都是整数值 0 或 1,其中 0 表示负面影评,1 表示正面影评。
print("Training entries: {}, labels: {}".format(len(train_data), len(train_labels)))Training entries: 25000, labels: 25000
影评文本已转换为整数,其中每个整数都表示字典中的一个特定字词。第一条影评如下所示:
print(train_data[0])
[1, 14, 22, 16, 43, 530, 973, 1622, 1385, 65, 458, 4468, 66, 3941, 4, 173, 36, 256, 5, 25, 100, 43, 838, 112, 50, 670, 2, 9, 35, 480, 284, 5, 150, 4, 172, 112, 167, 2, 336, 385, 39, 4, 172, 4536, 1111, 17, 546, 38, 13, 447, 4, 192, 50, 16, 6, 147, 2025, 19, 14, 22, 4, 1920, 4613, 469, 4, 22, 71, 87, 12, 16, 43, 530, 38, 76, 15, 13, 1247, 4, 22, 17, 515, 17, 12, 16, 626, 18, 2, 5, 62, 386, 12, 8, 316, 8, 106, 5, 4, 2223, 5244, 16, 480, 66, 3785, 33, 4, 130, 12, 16, 38, 619, 5, 25, 124, 51, 36, 135, 48, 25, 1415, 33, 6, 22, 12, 215, 28, 77, 52, 5, 14, 407, 16, 82, 2, 8, 4, 107, 117, 5952, 15, 256, 4, 2, 7, 3766, 5, 723, 36, 71, 43, 530, 476, 26, 400, 317, 46, 7, 4, 2, 1029, 13, 104, 88, 4, 381, 15, 297, 98, 32, 2071, 56, 26, 141, 6, 194, 7486, 18, 4, 226, 22, 21, 134, 476, 26, 480, 5, 144, 30, 5535, 18, 51, 36, 28, 224, 92, 25, 104, 4, 226, 65, 16, 38, 1334, 88, 12, 16, 283, 5, 16, 4472, 113, 103, 32, 15, 16, 5345, 19, 178, 32]
影评的长度可能会有所不同。以下代码显示了第一条和第二条影评中的字词数。由于神经网络的输入必须具有相同长度,因此我们稍后需要解决此问题。
len(train_data[0]), len(train_data[1])
(218, 189)
将整数转换回字词
了解如何将整数转换回文本可能很有用。在以下代码中,我们将创建一个辅助函数来查询包含整数到字符串映射的字典对象:
# A dictionary mapping words to an integer index
word_index = imdb.get_word_index()
# The first indices are reserved
word_index = {k:(v+3) for k,v in word_index.items()}
word_index[""] = 0
word_index[""] = 1
word_index[""] = 2 # unknown
word_index[""] = 3
reverse_word_index = dict([(value, key) for (key, value) in word_index.items()])
def decode_review(text):
return ' '.join([reverse_word_index.get(i, '?') for i in text])
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/imdb_word_index.json
1646592/1641221 [==============================] - 0s 0us/step
现在,我们可以使用 decode_review 函数显示第一条影评的文本:
decode_review(train_data[0])准备数据
影评(整数数组)必须转换为张量,然后才能馈送到神经网络中。我们可以通过以下两种方法实现这种转换:
-
对数组进行独热编码,将它们转换为由 0 和 1 构成的向量。例如,序列 [3, 5] 将变成一个 10000 维的向量,除索引 3 和 5 转换为 1 之外,其余全转换为 0。然后,将它作为网络的第一层,一个可以处理浮点向量数据的密集层。不过,这种方法会占用大量内存,需要一个大小为
num_words * num_reviews的矩阵。 -
或者,我们可以填充数组,使它们都具有相同的长度,然后创建一个形状为
max_length * num_reviews的整数张量。我们可以使用一个能够处理这种形状的嵌入层作为网络中的第一层。
在本教程中,我们将使用第二种方法。
由于影评的长度必须相同,我们将使用 pad_sequences 函数将长度标准化:
train_data = keras.preprocessing.sequence.pad_sequences(train_data,
value=word_index[""],
padding='post',
maxlen=256)
test_data = keras.preprocessing.sequence.pad_sequences(test_data,
value=word_index[""],
padding='post',
maxlen=256)
现在,我们来看看样本的长度:
len(train_data[0]), len(train_data[1])
(256, 256)
并检查(现已填充的)第一条影评:
print(train_data[0])
[ 1 14 22 16 43 530 973 1622 1385 65 458 4468 66 3941
4 173 36 256 5 25 100 43 838 112 50 670 2 9
35 480 284 5 150 4 172 112 167 2 336 385 39 4
172 4536 1111 17 546 38 13 447 4 192 50 16 6 147
2025 19 14 22 4 1920 4613 469 4 22 71 87 12 16
43 530 38 76 15 13 1247 4 22 17 515 17 12 16
626 18 2 5 62 386 12 8 316 8 106 5 4 2223
5244 16 480 66 3785 33 4 130 12 16 38 619 5 25
124 51 36 135 48 25 1415 33 6 22 12 215 28 77
52 5 14 407 16 82 2 8 4 107 117 5952 15 256
4 2 7 3766 5 723 36 71 43 530 476 26 400 317
46 7 4 2 1029 13 104 88 4 381 15 297 98 32
2071 56 26 141 6 194 7486 18 4 226 22 21 134 476
26 480 5 144 30 5535 18 51 36 28 224 92 25 104
构建模型
神经网络通过堆叠层创建而成,这需要做出两个架构方面的主要决策:
- 要在模型中使用多少个层?
- 要针对每个层使用多少个隐藏单元?
在本示例中,输入数据由字词-索引数组构成。要预测的标签是 0 或 1。接下来,我们为此问题构建一个模型:
# input shape is the vocabulary count used for the movie reviews (10,000 words)
vocab_size = 10000
model = keras.Sequential()
model.add(keras.layers.Embedding(vocab_size, 16))
model.add(keras.layers.GlobalAveragePooling1D())
model.add(keras.layers.Dense(16, activation=tf.nn.relu))
model.add(keras.layers.Dense(1, activation=tf.nn.sigmoid))
model.summary()
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
embedding (Embedding) (None, None, 16) 160000
_________________________________________________________________
global_average_pooling1d (Gl (None, 16) 0
_________________________________________________________________
dense (Dense) (None, 16) 272
_________________________________________________________________
dense_1 (Dense) (None, 1) 17
=================================================================
Total params: 160,289
Trainable params: 160,289
Non-trainable params: 0
_________________________________________________________________
按顺序堆叠各个层以构建分类器:
- 第一层是
Embedding层。该层会在整数编码的词汇表中查找每个字词-索引的嵌入向量。模型在接受训练时会学习这些向量。这些向量会向输出数组添加一个维度。生成的维度为:(batch, sequence, embedding)。 - 接下来,一个
GlobalAveragePooling1D层通过对序列维度求平均值,针对每个样本返回一个长度固定的输出向量。这样,模型便能够以尽可能简单的方式处理各种长度的输入。 - 该长度固定的输出向量会传入一个全连接 (
Dense) 层(包含 16 个隐藏单元)。 - 最后一层与单个输出节点密集连接。应用
sigmoid激活函数后,结果是介于 0 到 1 之间的浮点值,表示概率或置信水平。
隐藏单元
上述模型在输入和输出之间有两个中间层(也称为“隐藏”层)。输出(单元、节点或神经元)的数量是相应层的表示法空间的维度。换句话说,该数值表示学习内部表示法时网络所允许的自由度。
如果模型具有更多隐藏单元(更高维度的表示空间)和/或更多层,则说明网络可以学习更复杂的表示法。不过,这会使网络耗费更多计算资源,并且可能导致学习不必要的模式(可以优化在训练数据上的表现,但不会优化在测试数据上的表现)。这称为过拟合,我们稍后会加以探讨。
损失函数和优化器
模型在训练时需要一个损失函数和一个优化器。由于这是一个二元分类问题且模型会输出一个概率(应用 S 型激活函数的单个单元层),因此我们将使用 binary_crossentropy 损失函数。
该函数并不是唯一的损失函数,例如,您可以选择 mean_squared_error。但一般来说,binary_crossentropy 更适合处理概率问题,它可测量概率分布之间的“差距”,在本例中则为实际分布和预测之间的“差距”。
在回归问题(比如预测房价)时,用另一个称为均方误差的损失函数。
现在,配置模型以使用优化器和损失函数:
model.compile(optimizer=tf.train.AdamOptimizer(),
loss='binary_crossentropy',
metrics=['accuracy'])
创建验证集
在训练时,我们需要检查模型处理从未见过的数据的准确率。我们从原始训练数据中分离出 10000 个样本,创建一个验证集。(为什么现在不使用测试集?我们的目标是仅使用训练数据开发和调整模型,然后仅使用一次测试数据评估准确率。)
x_val = train_data[:10000]
partial_x_train = train_data[10000:]
y_val = train_labels[:10000]
partial_y_train = train_labels[10000:]
训练模型
用有 512 个样本的小批次训练模型 40 个周期。这将对 x_train 和 y_train 张量中的所有样本进行 40 次迭代。在训练期间,监控模型在验证集的 10000 个样本上的损失和准确率:
history = model.fit(partial_x_train,
partial_y_train,
epochs=40,
batch_size=512,
validation_data=(x_val, y_val),
verbose=1)
Train on 15000 samples, validate on 10000 samples
Epoch 1/40
15000/15000 [==============================] - 1s 53us/step - loss: 0.6916 - acc: 0.5907 - val_loss: 0.6894 - val_acc: 0.6462
Epoch 2/40
15000/15000 [==============================] - 1s 41us/step - loss: 0.6849 - acc: 0.7349 - val_loss: 0.6802 - val_acc: 0.7464
Epoch 3/40
15000/15000 [==============================] - 1s 40us/step - loss: 0.6711 - acc: 0.7663 - val_loss: 0.6632 - val_acc: 0.7627
Epoch 4/40
15000/15000 [==============================] - 1s 40us/step - loss: 0.6472 - acc: 0.7761 - val_loss: 0.6373 - val_acc: 0.7676
Epoch 5/40
15000/15000 [==============================] - 1s 39us/step - loss: 0.6133 - acc: 0.7973 - val_loss: 0.6016 - val_acc: 0.7887
Epoch 6/40
15000/15000 [==============================] - 1s 38us/step - loss: 0.5716 - acc: 0.8146 - val_loss: 0.5617 - val_acc: 0.8029
Epoch 7/40
15000/15000 [==============================] - 1s 38us/step - loss: 0.5259 - acc: 0.8329 - val_loss: 0.5202 - val_acc: 0.8204
Epoch 8/40
15000/15000 [==============================] - 1s 37us/step - loss: 0.4804 - acc: 0.8466 - val_loss: 0.4805 - val_acc: 0.8352
Epoch 9/40
15000/15000 [==============================] - 1s 40us/step - loss: 0.4387 - acc: 0.8589 - val_loss: 0.4454 - val_acc: 0.8442
Epoch 10/40
15000/15000 [==============================] - 1s 40us/step - loss: 0.4013 - acc: 0.8733 - val_loss: 0.4158 - val_acc: 0.8495
Epoch 11/40
15000/15000 [==============================] - 1s 41us/step - loss: 0.3697 - acc: 0.8810 - val_loss: 0.3934 - val_acc: 0.8542
Epoch 12/40
15000/15000 [==============================] - 1s 39us/step - loss: 0.3432 - acc: 0.8869 - val_loss: 0.3712 - val_acc: 0.8627
Epoch 13/40
15000/15000 [==============================] - 1s 39us/step - loss: 0.3192 - acc: 0.8941 - val_loss: 0.3556 - val_acc: 0.8679
Epoch 14/40
15000/15000 [==============================] - 1s 40us/step - loss: 0.2993 - acc: 0.8997 - val_loss: 0.3416 - val_acc: 0.8721
Epoch 15/40
15000/15000 [==============================] - 1s 38us/step - loss: 0.2820 - acc: 0.9046 - val_loss: 0.3307 - val_acc: 0.8736
Epoch 16/40
15000/15000 [==============================] - 1s 39us/step - loss: 0.2672 - acc: 0.9076 - val_loss: 0.3218 - val_acc: 0.8753
Epoch 17/40
15000/15000 [==============================] - 1s 39us/step - loss: 0.2528 - acc: 0.9143 - val_loss: 0.3143 - val_acc: 0.8774
Epoch 18/40
15000/15000 [==============================] - 1s 40us/step - loss: 0.2404 - acc: 0.9192 - val_loss: 0.3080 - val_acc: 0.8817
Epoch 19/40
15000/15000 [==============================] - 1s 41us/step - loss: 0.2289 - acc: 0.9227 - val_loss: 0.3028 - val_acc: 0.8816
Epoch 20/40
15000/15000 [==============================] - 1s 37us/step - loss: 0.2189 - acc: 0.9249 - val_loss: 0.2987 - val_acc: 0.8829
Epoch 21/40
15000/15000 [==============================] - 1s 39us/step - loss: 0.2089 - acc: 0.9293 - val_loss: 0.2951 - val_acc: 0.8834
Epoch 22/40
15000/15000 [==============================] - 1s 41us/step - loss: 0.1999 - acc: 0.9323 - val_loss: 0.2925 - val_acc: 0.8833
Epoch 23/40
15000/15000 [==============================] - 1s 41us/step - loss: 0.1916 - acc: 0.9351 - val_loss: 0.2907 - val_acc: 0.8840
Epoch 24/40
15000/15000 [==============================] - 1s 40us/step - loss: 0.1834 - acc: 0.9402 - val_loss: 0.2882 - val_acc: 0.8849
Epoch 25/40
15000/15000 [==============================] - 1s 41us/step - loss: 0.1761 - acc: 0.9431 - val_loss: 0.2868 - val_acc: 0.8853
Epoch 26/40
15000/15000 [==============================] - 1s 40us/step - loss: 0.1688 - acc: 0.9459 - val_loss: 0.2864 - val_acc: 0.8857
Epoch 27/40
15000/15000 [==============================] - 1s 38us/step - loss: 0.1628 - acc: 0.9490 - val_loss: 0.2861 - val_acc: 0.8859
Epoch 28/40
15000/15000 [==============================] - 1s 42us/step - loss: 0.1562 - acc: 0.9520 - val_loss: 0.2854 - val_acc: 0.8866
Epoch 29/40
15000/15000 [==============================] - 1s 39us/step - loss: 0.1503 - acc: 0.9536 - val_loss: 0.2854 - val_acc: 0.8866
Epoch 30/40
15000/15000 [==============================] - 1s 40us/step - loss: 0.1451 - acc: 0.9556 - val_loss: 0.2861 - val_acc: 0.8864
Epoch 31/40
15000/15000 [==============================] - 1s 41us/step - loss: 0.1390 - acc: 0.9585 - val_loss: 0.2870 - val_acc: 0.8872
Epoch 32/40
15000/15000 [==============================] - 1s 41us/step - loss: 0.1342 - acc: 0.9604 - val_loss: 0.2883 - val_acc: 0.8867
Epoch 33/40
15000/15000 [==============================] - 1s 40us/step - loss: 0.1287 - acc: 0.9631 - val_loss: 0.2896 - val_acc: 0.8869
Epoch 34/40
15000/15000 [==============================] - 1s 40us/step - loss: 0.1242 - acc: 0.9647 - val_loss: 0.2911 - val_acc: 0.8856
Epoch 35/40
15000/15000 [==============================] - 1s 41us/step - loss: 0.1200 - acc: 0.9656 - val_loss: 0.2925 - val_acc: 0.8873
Epoch 36/40
15000/15000 [==============================] - 1s 39us/step - loss: 0.1150 - acc: 0.9681 - val_loss: 0.2949 - val_acc: 0.8851
Epoch 37/40
15000/15000 [==============================] - 1s 40us/step - loss: 0.1110 - acc: 0.9694 - val_loss: 0.2972 - val_acc: 0.8852
Epoch 38/40
15000/15000 [==============================] - 1s 40us/step - loss: 0.1075 - acc: 0.9697 - val_loss: 0.2993 - val_acc: 0.8840
Epoch 39/40
15000/15000 [==============================] - 1s 40us/step - loss: 0.1030 - acc: 0.9715 - val_loss: 0.3016 - val_acc: 0.8826
Epoch 40/40
15000/15000 [==============================] - 1s 40us/step - loss: 0.0991 - acc: 0.9731 - val_loss: 0.3042 - val_acc: 0.8842
评估模型
我们来看看模型的表现如何。模型会返回两个值:损失(表示误差的数字,越低越好)和准确率。
results = model.evaluate(test_data, test_labels)
print(results)
25000/25000 [==============================] - 1s 35us/step
[0.32395469411849975, 0.87264]
使用这种相当简单的方法可实现约 87% 的准确率。如果采用更高级的方法,模型的准确率应该会接近 95%。
创建准确率和损失随时间变化的图
model.fit() 返回一个 History 对象,该对象包含一个字典,其中包括训练期间发生的所有情况:
history_dict = history.history
history_dict.keys()
dict_keys(['loss', 'val_loss', 'val_acc', 'acc'])
一共有 4 个条目:每个条目对应训练和验证期间的一个受监控指标。我们可以使用这些指标绘制训练损失与验证损失图表以进行对比,并绘制训练准确率与验证准确率图表:
import matplotlib.pyplot as plt
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(acc) + 1)
# "bo" is for "blue dot"
plt.plot(epochs, loss, 'bo', label='Training loss')
# b is for "solid blue line"
plt.plot(epochs, val_loss, 'b', label='Validation loss')
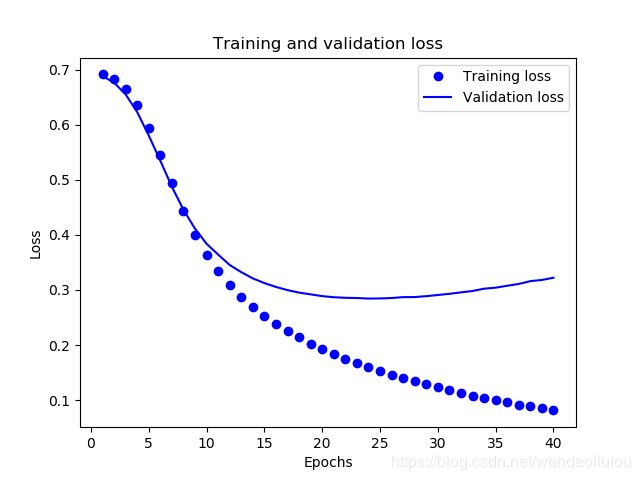
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
plt.clf() # clear figure
acc_values = history_dict['acc']
val_acc_values = history_dict['val_acc']
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()
在该图表中,圆点表示训练损失和准确率,实线表示验证损失和准确率。
可以注意到,训练损失随着周期数的增加而降低,训练准确率随着周期数的增加而提高。在使用梯度下降法优化模型时,这属于正常现象 - 该方法应在每次迭代时尽可能降低目标值。
验证损失和准确率的变化情况并非如此,它们似乎在大约 20 个周期后达到峰值。这是一种过拟合现象:模型在训练数据上的表现要优于在从未见过的数据上的表现。在此之后,模型会过度优化和学习特定于训练数据的表示法,而无法泛化到测试数据。
对于这种特殊情况,我们可以在大约 20 个周期后停止训练,防止出现过拟合。