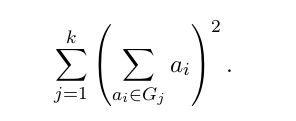数组分块使平方和最小

题目是这样子的:
You are given as input a sequence of n positive
integers a 1 , a 2 , . . . , a n and a positive integer k ≤ n. Your task is to group
these numbers into k groups of consecutive numbers, that is, as they appear
in the input order a 1 , a 2 , . . . , a n , so as to minimise the total sum of the
squares of sums of these numbers within each group.
More formally, you have to decide the k − 1 cutting positions 1 ≤ i 1 <
i 2 < · · · < i k−1 ≤ n − 1, where (we assume below that i 0 = 1):
• group G 1 is defined as G 1 = {a 1 , a 2 , · · · , a i 1 }
• group G j , for j = 2, 3, . . . , k − 1, is defined as
G j = {a i j−1 +1 , a i j−1 +2 , · · · , a i j }
• group G k is defined as G k = {a i k−1 +1 , a i k−1 +2 , · · · , a i k }
Then, such feasible solution, that is, grouping into these k groups, has the
value of the objective function equal to

equation.png

Your goal is to find such grouping into k groups so that this objective func-
tion is minimised.
Suppose, for instance, that n = 5 and k = 3 and that input sequence is:
5 7 11 4 21,
that is, a 1 = 5, a 2 = 7, a 3 = 11, a 4 = 4, a 5 = 21. Then, for example, setting
the k − 1 = 2 cutting positions as follows
5 7 | 11 | 4 21,
that is the cutting positions i 1 = 2, i 2 = 3, define the following k = 3 groups
G 1 = {5, 7}, G 2 = {11}, G 3 = {4, 21}. The objective function value of this
grouping is
(5 + 7) 2 + (11) 2 + (4 + 21) 2 = 144 + 121 + 625 = 890.
Observe that there is a better solution here, with the following grouping
5 7 | 11 4 | 21,The objective function value of this grouping is
(5 + 7) 2 + (11 + 4) 2 + (21) 2 = 144 + 225 + 441 = 810,
and it can be checked that this is the optimal grouping, that is, 810 is the
smallest possible value of the objective function among all possible groupings
in this instance.
For further examples of inputs together with values of their optimal
solutions, see the text file data2.txt that I provide (see explanation of the
data format below). In fact the example sequence above, 5 7 11 4 21, with
k = 3 is the first instance in data1.txt and in data2.txt (data2.txt contains
also solutions).
Observe that the input sequence a 1 , . . . , a n need not be sorted and you
are not supposed to change the order of these numbers, but only find ap-
propriate k − 1 cut points that define the k groups (each group must be
non-empty, that is, must contain at least one number). The task is, given
any sequence of n (strictly) positive integers and k ≤ n, find the grouping
that has the smallest possible objective function value. Note that the input
sequence may contain the same number multiple times.
Also observe that it is possible that k = n in the input to this problem
(it is impossible that k > n, though). For instance if the input sequence is
as above
5 7 11 4 21,
and k = n = 5, then there exists only one possible feasible grouping into
k = 5 groups with the following cut points:
5 | 7 | 11 | 4 | 21,
and the objective value of this grouping is
(5) 2 + (7) 2 + (11) 2 + (4) 2 + (21) 2 = 25 + 49 + 121 + 16 + 441 = 652,
and this is the (optimal) solution to this instance with k = 5.
You should write a procedure that for any given input sequence of n
positive integers and any given k ≤ n, finds a grouping with minimum
value of the objective function value. Your procedure should only output
the value of the objective of this optimal solution (grouping). That is, it
should compute the grouping with minimum possible value of the objective
function among all feasible groupings, and then output the objective value
of this optimal grouping.
Additionally, you should include a brief idea of your solution in the
commented text in your code and you should also include a short analysis
and justification of the running time of your procedure. These descriptions
are part of the assessment of your solution.

题目说了一堆,举个例子一目了然:
输入 5 7 11 4 21, k = 3 (分三组)
最优解为 (5 + 7) 2 + (11 + 4) 2 + (21) 2 = 144 + 225 + 441 = 810

我的思路:

每次分出一组数据，随意挑一个位置给一刀,分成两部分,只有两种情况，要么把左边的数据单独作为一组,要么把右边的数据单独作为一组，剩下的数据继续划分为ｋ- 1组．
　　形式化表示如下:
divide(A, start, end, k) =
　　min {
　　　　 min {divede(A, i + 1, end, k) + divide (A, start, i, 1)},
　　　　 { min {divide(A, start, i - 1, k)} + divide(A, i, end, 1) }
}
(start为可以划分的第一个位置，end为可以划分的最后一个位置,i的取值范围为start -> end)
明显,用递归就可以求出最优解,但这样计算复杂度非常高,因为重复求和，重复去划分数组,这样的复杂度是斐波拉契级数的阶乘复杂度,这个复杂度无法想象,数据稍微多一点,我的小破笔记本根本跑不出来，20对个数据分20组估计可以让我电脑跑个把小时，没具体算,估计更久．

于是,先用一个一维数组保存求和结果,再用一个三维数组保存求最优解的结果．这样下次求和时可以直接得出结果，也避免了重复计算最优解．
求和的复杂度是0(n), 三维数组全部填满的复杂度是0(n^2 * k),这里采用了动态规划的思想,计算规模会从小到大.
所以,最终复杂度是0(n) + 0(n^2 * k)

代码如下:

import java.io.IOException;
import java.nio.charset.Charset;
import java.nio.file.Files;
import java.nio.file.Paths;
import java.util.ArrayList;
import java.util.List;

public class Divide {
    //保存求和结果, 避免每次都去计算
    private static int[] sumArr;
    //保存分组结果
    private static int[][][] result;

    private int divide(int[] number, int start, int end, int k) {
        if (k == 1) {
            return calSum(number, start, end) * calSum(number, start, end);
        }

        int min = Integer.MAX_VALUE;
        int temp = 0;
        int i;
        for (i = start; i <= end; i++) {

            int resultOfSum1 = Integer.MAX_VALUE;
            if (end - i >= k - 1) {
                resultOfSum1 = result[i + 1][end][k - 1] > 0 ? result[i + 1][end][k - 1] : divide(number, i + 1, end, k - 1);
                result[i + 1][end][k - 1] = resultOfSum1;
                resultOfSum1 += divide(number, start, i, 1);
            }


            int resultOfSum2 = Integer.MAX_VALUE;
            if (i - start >= k - 1) {
                resultOfSum2 = result[start][i - 1][k - 1] > 0 ? result[start][i - 1][k - 1] : divide(number, start, i - 1, k - 1);
                result[start][i - 1][k - 1] = resultOfSum2;
                resultOfSum2 += divide(number, i, end, 1);
            }

            temp = resultOfSum1 < resultOfSum2 ? resultOfSum1 : resultOfSum2;

            if (temp < min) {
                min = temp;
            }
        }
        return min;
    } // end of procedure divide

    private int calSum(int[] A, int start, int end) {
        if (start == 0) {
            return sumArr[end];
        }
        return sumArr[end] - sumArr[start - 1];
    }

    private void test(String filePath) {
        List> data = readData(filePath);
        int corectAmount = 0;
        for (List testData : data) {
            //分组数
            int k = testData.get(0);
            //结果
            int result = testData.get(1);
            int[] number = new int[testData.size() - 2];
            for (int i = 2; i < testData.size(); i++) {
                number[i - 2] = testData.get(i);
            }
            if (result == compute(number, k)) {
                corectAmount++;
            }
        }
        System.out.printf("正确率: %.2f", corectAmount * 100.0 / data.size());
    }

    private int compute(int[] number, int k) {
        sumArr = new int[number.length];
        result = new int[number.length][number.length][k];
        sumArr[0] = number[0];
        for (int i = 1; i < number.length; i++) {
            sumArr[i] = number[i] + sumArr[i - 1];
        }
        return divide(number, 0, number.length - 1, k);
    }


    /**
     * 每组数据用A分隔,第一行为分组数,第二行为最优解,剩余部分为输入的数据
     *
     * @param filePath
     * @return
     */
    private List> readData(String filePath) {
        List> data = new ArrayList<>();
        List lines = null;
        try {
            lines = Files.readAllLines(Paths.get(filePath), Charset.defaultCharset());
        } catch (IOException e) {
            e.printStackTrace();
        }
        if (lines == null) {
            return null;
        }
        List temp = new ArrayList<>();
        for (String line : lines) {
            if (line.equals("A")) {
                data.add(temp);
                temp = new ArrayList<>();
                continue;
            }
            temp.add(Integer.valueOf(line));
        }
        return data;
    }


    public static void main(String[] args) {
        new Divide().test(args[0]);
    }
}

测试数据如下:
每组数据用A分隔,第一行为分组数,第二行为最优解,剩余部分为输入的数据

数组分块使平方和最小

我的思路:

代码如下:

你可能感兴趣的:(数组分块使平方和最小)