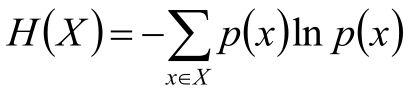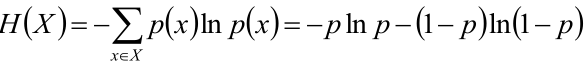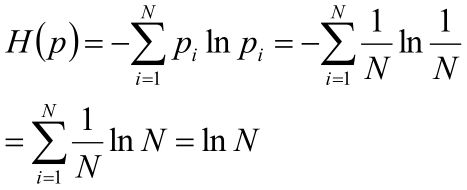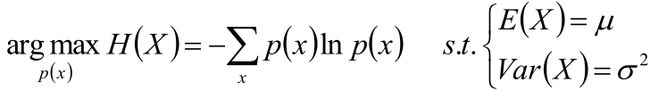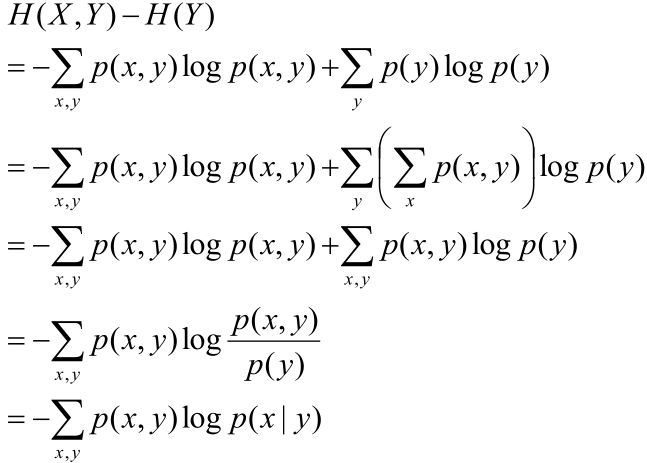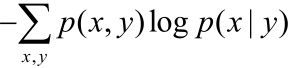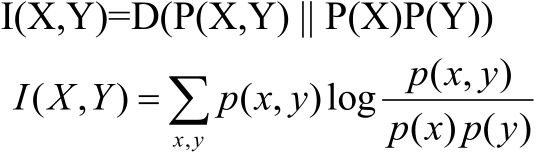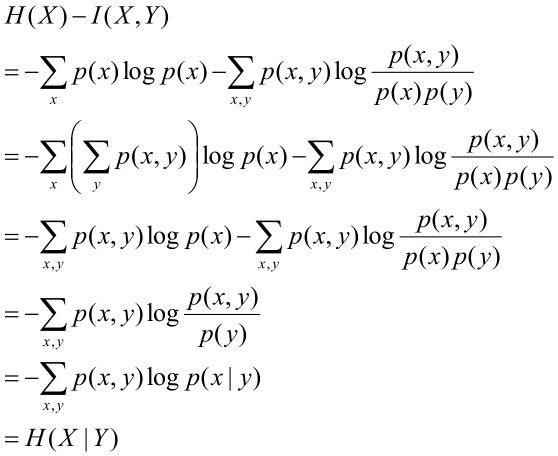最大熵模型(第二次总结)
本总结是是个人为防止遗忘而作,不得转载和商用。
说明:此篇是作者对“最大熵模型”的第二次总结,因此可以算作对上次总结的查漏补缺以及更进一步的理解,所以很多在第一次总结中已经整理过的内容在本篇中将不再重复,如果你看的有些吃力,那建议你看下我的第一次总结:
http://blog.csdn.net/xueyingxue001/article/details/50773796
信息量:
某事件x的信息量的式子为:
h(x)= -log2x 式1
关于此式的一个欧拉式解释如下:
某事件发生的概率小,则该事件的信息量大。如:一学生本来都是提前到教室,结果就某天迟到了,那迟到这个概率小的事件,其信息量一定很大。
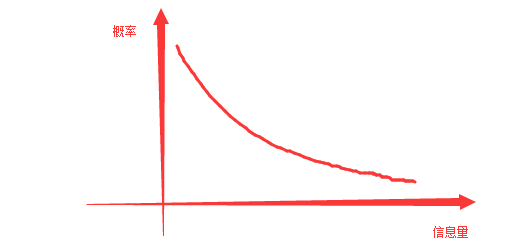
于是上面的话反映到坐标轴就是:
因此信息量h(x)应该是个递减的式子
话说对于两个独立事件x和y有P(xy) =p(x)p(y),然后假定它们的信息量分布是h(x)和h(y),于是这两个事件的信息量h(xy)应该是类似h(x)h(y)这样的式子,但如果可以把两个事件的信息量h(xy)写成h(x)+h(y)的形式就好了,于是取对数,这样把“对数、递减”这几个因素合起来就有了式1。
PS:注意,这是个欧拉式的解释。
熵:
举个例子,假设x只能取0和1这两个值,然后取这两个值的概率分别为:
P(x= 0) = 0.3
p(x= 1) = 0.7
于是这两个取值的信息量就分别是:
H(x=0)= -log20.3
H(x=1)= -log20.7
既然如此,x平均下来的信息量是多大呢?
你看,x=0的信息量有0.3的概率发生,x=1的信息量有0.7的概率发生,于是P(x =0) H(x=0) + p(x = 1) H(x=1)就是x的一个平均化的信息量。
而熵就是这个平均化的信息量,将其写成公式的话就是:
注:经典熵的定义,底数是2,单位是bit;若底数是e,单位是nat(奈特)。
两点分布的熵:
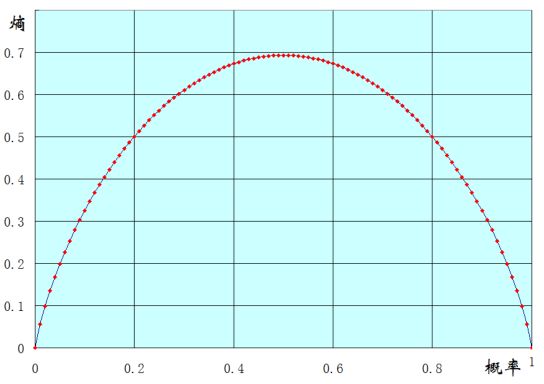
下面是两点分布熵的图:
从图中可以看出:
概率为1和概率为0的熵为0,举个例子:x=0发生的概率为0,x=1发生的概率为1,这样一来,我说“x=0一定不发生”和“x=1一定发生”那都是废话,完全没信息量。
三点分布的熵
均匀分布的熵
因为均匀分布的熵最大,所以0≤H(X)≤lnN。
给定方差的最大熵分布
1,建立目标函数
2,使用方差公式化简约束条件
Var(X)= E(X2) - E2(x)
=>E(X2) = E2(X) + Var(X) =μ2 +σ2
3,更新目标函数
4,因为这就是个带约束的极值问题,所以利用Lagrange乘子法
5,因为p(x)的对数是二次函数,所以p(x)一定是正态分布(原因见我总结的“根据函数形式判断概率分布”)。
联合熵
两个随机变量X,Y的联合分布,可以形成联合熵JointEntropy,用H(X,Y)表示。
条件熵
(X,Y)发生所包含的熵,减去Y单独发生包含的熵,即:在Y发生的前提下,X发生“新”带来的熵,用H(X,Y)– H(Y) 表示,可以简写成H(X|Y)。
条件熵定义式的推导过程为(结论就是定义式):
到这里就需要说点东西了,如果把熵和联合熵的求和符号和符号去掉的话,那剩余的部分:
熵 :p(x)logp(x)
联合熵 :p(x,y)logp(x,y)
怎么到了条件熵后其剩余的部分变成:p(x,y)logp(x|y)了?按照上面的“规律”不该是p(x|y)logp(x|y)吗?
其实是这样,看下图:
推导解释:
①:既然H(X|Y),即H(X,Y) –H(Y)可以写成
那将H(X|Y)换成H(Y|X)后就得出第一个等号了。
②:将求和符号分开
③:条件概率公式
④:p(x)中只有x,和y没关系,所以移动下位置
⑤:稍微做下变换,这个疑惑的话用冷水洗洗脸,
⑥:注意看⑤的p(x)后面的那部分:这不就是x给定的情况下y的熵嘛!于是⑥式得出!
好了,上面的推导解释完了,下面我们分析下结果。
结果,即⑥式的意思是什么?
是“对‘x给定的情况下y的熵’相对于x求期望”,这就是条件熵的含义!
所以才会有相对于熵来说有点不同的式子。
相对熵
相对熵,又称互熵,交叉熵,鉴别信息,Kullback熵,Kullback-Leible散度等。
注:在相对熵的定义中,如果p和q都是概率密度时,上面这些名字才都是一个东西。
定义:
设p(x)、q(x)是X中取值的两个概率分布,则p对q的相对熵是
PS1,第二个等号的含义是:再将log(p(x)/q(x))看成一个整体的情况下,相对熵相当于对log(p(x)/q(x))在p(x)上求期望。
PS2:对于凸函数,D(p||q)≥0,D(q||p)≥0。
作用:
相对熵可以度量两个随机变量的“距离”
但,除非p和q相等,否则D(p||q)≠D(q||p),即p到q的“距离”≠q到p的“距离”,打个比方的话就好像:p在上游,q在下游,那p到q就容易,q到p就不容易。
KL散度
首先还是先说明一点:这里的KL散度就是相对熵,只不过在听课时一直在说“KL散度”而不在用“相对熵”这个名字来称呼这个知识,所以就将其列成一个大章节了。
首先,先来几个问答。
Q1:为什么需要KL散度?
A1:有时候我们需要面对这样的情况 --假定已知随机变量P,求相对简单的随机变量Q,使得Q尽量接近P。这时KL散度就派上用场了。
Q2:使用KL散度时有什么难点呢?
A2:从上面的相对熵知道,K-L距离是非对称的,于是到底应该选KL(Q||P)还是KL(P||Q)就需要考虑了。
Q3:KL(Q||P)和KL(P||Q) 选择判断上有什么区别?
A3:
1, 假定使用KL(Q||P),为了让距离最小,则要求在P为0的地方,Q尽量为0。会得到比较“窄”的分布曲线(因为图形曲线的积分面积要为1(还记得吗?p和q都是概率密度),所以既然P为0的地方,Q都尽量为0了,那剩下不为0的地方就会很高,于是很窄);
假定使用KL(P||Q),为了让距离最小,则要求在P不为0的地方,Q也尽量不为0。会得到比较“宽”的分布曲线;
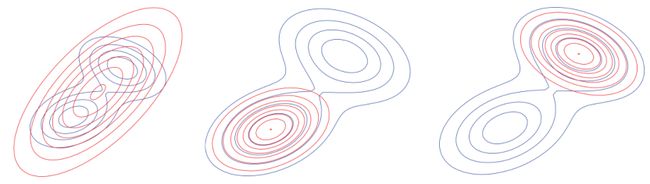
2, 如下图所示:
蓝色是P的曲线(假设P有两个峰)
中、右图是KL(Q||P),因为是Q真对P,所以Q能够锁定P的一个峰值
左图是KL(P||Q),因为是P针对Q,所以Q倾向于覆盖P,就不容易锁定P的一个峰值。
互信息
定义:
两个随机变量X,Y的互信息,定义为X,Y的联合分布和独立分布乘积的相对熵。
公式:
话说,“熵 -互信息 = 条件熵”,原因见下面的公式:
因此有些文献也将互信息I(X,Y)定义为 H(Y) - H(Y|X)
整理下上面的等式
然后根据上图中的式子可以推导出: H(X|Y)≤ H(X),H(Y|X)≤ H(Y)
其实这个可以解释:因为H(X)代表X的不确定度,H(X|Y)代表给定Y之后X的不确定度,如果X和Y有点联系,则H(X|Y)< H(X),如果X和Y没联系,则H(X|Y) = H(X),因此H(X|Y)≤ H(X);H(Y|X)≤ H(Y) 同理。
强大的Venn图:帮助记忆
![]()
这个图总结了所有的关系。
比如:如果互信息为0,则X和Y互相独立,因而也就有这个式子:
I(X,Y) = 0 意味着
P(X, Y) = P(X)P(Y) 和 P(X|Y) =P(X)