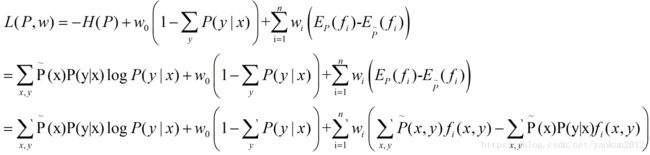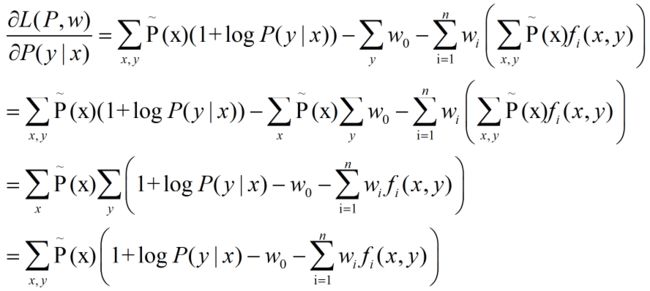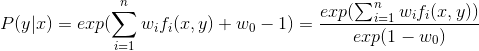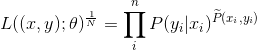关于最大熵模型的一些见解

1. 前言

本文主要涉及最大熵模型中的一些推导，旨在理顺内部之间的逻辑关系

求解目的：获取最好的模型

2. 最大熵原理

最大熵原理是概率模型学习的一个准则，最大熵原理认为，学校概率模型时，在所有可能的概率模型中，熵最大的模型是最好的模型。最大熵原理任务要选择的概率模型首先必须满足已有的事实，即约束条件。在没有更多信息的情况下，那些不确定的部分都是等可能的。最大熵原理通过熵的最大化来表示等可能性。结合求解的目的可知，当前的求解目标变为求解熵最大的模型。由此引出了两个问题：（1）什么是熵？ （2）怎么求解？

1. 什么是熵？

参考5.2.2 信息增益，可知熵的定义式：                        

(1.1)

结合例6.1可知，不确定条件的等可能假设使熵最大

 

 

在这里我们进一步得出了X给定条件下Y的条件概率分布

假设分类模型是一个条件概率分布，结合熵的定义，定义在条件概率分布上的条件熵为：

(1.2)

 

观察公式，有一个疑问，是什么意思？它来源于训练数据集，如果给我们一个数据集让我们获取一个模型，那么我们可以从数据集中获取一些有价值的信息，例如，联合分布的经验分布、边缘分布的经验分布。因此式1.2中，只是的函数（类似）。

前文设定最优模型是在熵取最大值时取得。又假设是分类模型，那么问题就转化为求解使熵取最大值时的分类模型，即使1.2式取最大值时的。最大熵问题转化为求使最大的

实际上，对一个模型求解问题，不可能仅利用一个公式既可，它还包含很多的约束条件：比如，我们用一个训练数据集去求解一个模型，那么求解出的这个模型必须符合数据集的规律，否则训练毫无意义（不符合数据集规律的模型有无数种）。

怎样用公式表达出这个含义？

//数学公式表示该约束条件\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

引入特征函数的概念，特征函数描述输入x和输出y之间的某一个事实：

                                        

特征函数关于经验分布的期望值:                

(1.3)

特征函数关于模型与经验分布的期望值:

(1.4)

（注意：对于条件概率，有。这个公式是用近似代替）

如果模型和训练数据集相适应，那么必然有。这就是前边说的约束条件，满足这些约束条件的的所有模型构成了模型集合：

(1.5)

求解的目的就是从C中找出熵最大的模型。

//数学公式表示该约束条件\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

还有一个约束条件为对于模型而言，所有可能发生的概率之和为1：

(1.6)

    2. 怎么求解？

求解问题：满足约束条件的模型构成一个模型集合（条件），从中找出对应熵最大的那个模型。

最大熵模型的学习过程就是求解最大熵模型的过程，最大熵模型的学习过程可以形式化为约束最优化问题：

(1.7)

按照最优化问题的习惯，将求最大值问题改写为等价的求最小值问题(提出一个“-”)：

(1.8)

对上式（1.8）引入拉格朗日乘子，定义拉格朗日函数：

求解，其中，为拉格朗日乘子

(1.9)

结合对偶问题可得，最优化的原始问题是：

(1.10)

对偶问题是：

(1.11)

由于原始问题满足凸优化理论中的KKT条件，因此原始问题的解和对偶问题的解是一致的。这样我们对原始问题（1.9/1.10）的求解变成了对拉格朗日对偶问题（1.11）的求解。

在求解对偶问题1.11时，是先求解内部的，再对其解关于w求最大值，记：

(1.12)

（注意：这里需要理解是在模型集合C中找出一个最小的P，那么说明它的解是一个P的表达式，这个P是关于w的函数）

设就是中关于P的最小解。（先假设最小解是这个表达式）

式1.11中首先对求解关于的最小值，对关于求偏导：

(1.13)

令偏导=0，而当时，只有括号内=0才可，故得：

(1.14)

又有等式约束，将上式中解得的带入约束：

这是对w的约束，化简上式：

(1.15)

（注意：这里不是y的函数，相当于一个常量，所以不需要在分式下方添加求和符号）

令

(1.16)

由1.15和1.16得

(1.17)

将1.17带入1.14得

(1.18)

这就是式1.12中的表达式，也是所谓的最大熵模型

结合1.11，1.12考虑对偶问题：

(1.19)

式1.19中的由式1.18给出，那么这种求解的逻辑关系为

原始问题对偶问题进而转换为求解

(1.20)

至此，第二个问题：怎么求解就转换为怎么求解。由此，我们设定第三个问题：怎么求解？

书中的办法是将其转换为最大熵模型的极大似然估计，由此第三个问题又转换出了两个问题：4.怎么证明对偶函数的极大化问题即与最大熵模型的极大似然估计间的等价关系；5.转换完之后怎么求（假设二者确实等价）？

这里先证明第4个问题，即对偶函数的极大化等价于最大熵模型的极大似然估计[1]

//等价关系证明\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

首先，对于条件概率的似然函数:

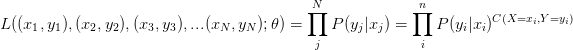(1.21)

这里，连乘符号上方N区分大小写:大写N表示训练数据集X中样本点的总个数；小写n表示X的取值个数，即合并相同样本点后的数量，表示的点出现的频数。如果我们对式1.21开N次方，即

 

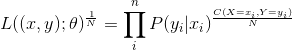(1.22)

而表示的是经验概率在的取值，即

(1.23)

那么式1.22化简为

(1.24)

对似然函数1.24取对数：

(1.25)

当条件概率分布是最大熵模型1.18时，将前文求解出的带入上式，得

(1.26)

（注意：不要忘记最初的问题是求解）

对于对偶问题,由1.9和1.12可得

(1.27)

对比1.26和1.27，发现二者相同，说明

(1.28)

等式关系得证，说明对偶函数的极大化等价于最大熵模型的极大似然估计。

//等价关系证明\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

至此，求解最优模型最终转化为最大熵模型的极大似然估计：

(1.29)

第5个问题就是求解上式。具体为6.3节中的各种算法[4]

 

 

参考：

[1].最大熵模型中的对数似然函数的解释

[2].Maximum Entropy Model最大熵模型

[3].最大熵模型原理小结

[4]. 统计学习方法.李航