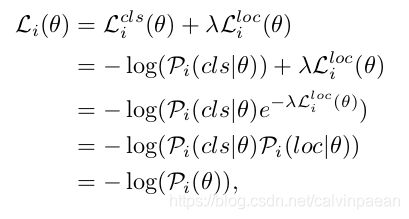AutoAssign 论文学习

Abstract

本文中，作者通过一种完全可微的标签分配策略，提出了一个anchor-free的目标检测器，叫做AutoAssign。通过产生正的和负的权重映射，动态调整每个位置的预测，它可以自动地判断正/负样本。作者提出了一个中心加权模块，调节具体类别的先验分布，以及一个置信度加权模块来调整每个实例的标签策略。整个标签分配的过程是可微的，无需额外修改就可迁移到其它数据集和任务上。在MS COCO数据集上的实验表明，该方法要比目前最佳的采样策略高$\sim 1\%$AP。而且，本文的最佳模型可以取得$52.1\%$的AP，超越现有的单阶段检测器。此外，在PASCAL VOC、Objects365和WiderFace 数据集上，AutoAssign 也展现了很强的应用性。

1. Introduction

目前 state of the art 的目标检测器都采用常见的密集预测的方式。双阶段（RPN部分）和单阶段检测器在每个CNN特征的位置上，通过不同尺度、宽高比和类别，以一种正规的、密集采样的方式来预测物体。而且，由于当前基于CNN的目标检测器通常采用多尺度的特征（例如FPN）来缓解尺度差异，标签分配就不仅要在空间特征图上选择位置，也要选择合适的特征层级尺度。

如图1所示，现有的检测器主要基于人为的前验，选择正样本和负样本：(1) 基于anchor的检测器如RetinaNet会预设一些anchors，它们在每个位置上的尺度和宽高比不同，需要借助IOU在空间和尺度层级的特征图上选取正样本和负样本。(2) anchor-free 检测器如FCOS，会采样每个物体中心区域的固定比例大小，作为空间正样本，然后通过预先设置的尺度约束来选择FPN的某个阶段。这些检测器按照物体的前验分布来设计它们的标签策略，在VOC和COCO benchmarks上也是非常有效的。

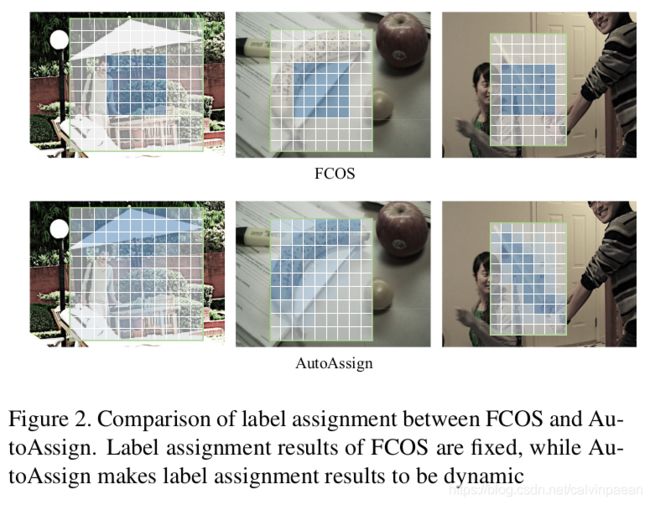
但是，如图2所示，在现实世界中，不同类别和场景的物体的外观差异很大。固定的中心采样策略可能会将物体外边的位置选作正样本。直觉上说，采样物体上的位置要比单纯的背景好，因为这些位置更容易输出较高分类置信度。另一方面，尽管CNN可以学习偏移量，但当背景被选做正样本时，这些特征就会不利于模型的表现。

因此，上述固定的策略可能就不会在空间和尺度维度上选择最适合的位置。除了人为设计的策略之外，最近一些工作提出了部分依赖于数据和动态标签分配的策略。GuidedAnchoring和MetaAnchor 会在采样之前，动态地调整 anchor 先验的形状，而其它的方法则在空间或尺度维度上，自适应地调整每个物体的采样策略。这些策略只会将部分的标签分配变为数据驱动的，而其余部分仍然受到人为设计的约束，阻碍标签分配的进一步优化。

本文中，作者提出了一个完全可微的标签分配策略。如图1所示，作者遵循 anchor-free 的方式（如FCOS）直接预测每个位置的目标，没用人为设计的anchors。为了保留足够多的位置进一步优化，在所有的尺度层级上，作者首先将一个边框内的所有点看作为正负候选样本。然后在训练损失函数中，依据所产生的正负权重图来修改预测。为了适应不同类别和尺度内的分布，作者提出了一个类别加权模块，叫做中心加权，来学习每个类别的分布。为了适应每个实例的外观和尺度，作者提出了一个置信度加权模块，调节空间和尺度维度上每个位置的正负置信度。然后，作者将两个模块结合起来，产生所有位置的正负权重图。整个加权过程是可微的，因此可以通过反向传播来优化。

总之，本文的贡献有三个方面：

1. 针对密集目标检测，提出了一个新的可微的标签分配策略，叫做AutoAssign，它自动地对每个实例分配正负样本。而且，该方式可以迁移到不同的数据集和任务上。
2. 提出了2个加权模块（中心加权和置信度加权），在空间和尺度维度上自适应地调节类别分布，以及实例采样策略。
3. 在COCO数据集和其他数据集上，进行了广泛的实验，证明AutoAssign的有效性。

2. Related Work

2.1 Fixed Label Assignment

经典的目标检测器通过预先判定的策略来采样正负样本。Faster R-CNN中的RPN会在每个位置上根据不同的尺度和宽高比，预先设定一些anchors。然后对于每个实例，计算 anchor 的 IOU 来指导其在尺度和空间维度上的标签。该基于anchor的策略迅速地主导了当前的检测器，并扩展至多尺度的输出特征，如YOLO、SSD和RetinaNet。最近学术圈开始关注anchor-free的检测器，无需设定anchor。FCOS摒弃了先验anchor设定，直接将每个物体的边框中心点附近的区域视作正样本。在尺度维度，它们会预先定义每个FPN阶段的尺度范围，从而标注每个实例。基于anchor和anchor-free的策略都需要数据分布的先验中心区域，边框中心点附近的空间位置更可能包含物体。

其它的anchor-free检测器则利用了不同的原理，将边框看作为关键点，将回归任务变换为热力图上的分类。这类检测器的特征与基于边框回归的检测器囧然不同。因此不在本文考虑范围内。

2.2 动态标签分配

由于固定的分配策略对于多样化的目标分布并不会是最优的，近来一些目标检测器提出了自适应机制，改进标签分配。GuidedAnchoring 利用语义特征来指导anchor设定，动态调整anchor的形状来适应不同的物体分布，而 MetaAnchor 则在训练过程中随机选取任意形状的 anchor，来覆盖不同类别的物体边框。除了改变anchor先验，另一些工作则直接对每个物体的采样策略做修改。FSAF 通过最小的训练损失值，动态将每个实例分配至最适合的FPN特征层级。SAPD 则对anchor正样本进行重新加权，使用额外的meta-net 来选择合适的FPN阶段。FreeAnchor 会基于每个物体的IOU，构建top-k个anchor候选框，然后使用Mean-Max函数来对选中的anchors加权，[9]设计了另一个加权函数来去除无效的anchors。ATSS 通过动态IOU阈值，根据实例的统计特征，提出了一个自适应的训练样本选取机制。

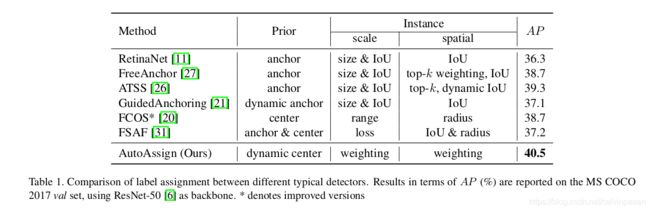
为了从一个更加全面的角度来展示现有的标签分配策略，作者在表1中列出了一些代表性方法的核心组建，一些是与先验有关的，另一些是与实例有关的。很清楚，与基于启发式学习的 RetinaNet 和 FCOS 不同，现有的动态策略中，标签分配中只有部分构成是数据驱动的。相反，其它的部分则依然依照了人工规则。

3. AutoAssign

3.1 Overview

AutoAssign 以完全的数据驱动的方式处理标签分配问题。它从零开始构建，没有任何传统的构成，如 anchors、IoU阈值、top-k或尺度范围。它直接使用网络的预测来动态调节每个位置正负样本的置信度。

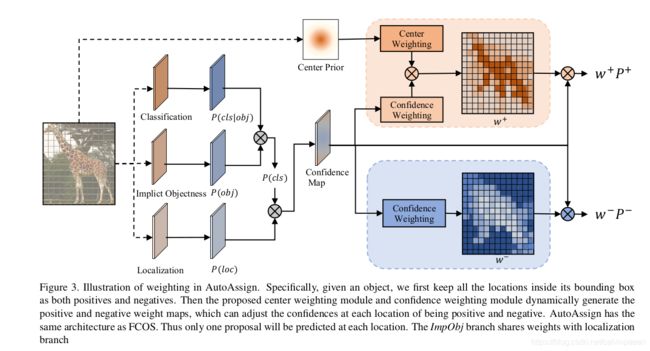
为了优化整个标签分配过程，作者提出了一个完全可微的策略，在空间和尺度维度上动态调节具体类别和具体实例的采样策略。在图3中展示了该策略的框架。作者首先采用anchor-free的方式来摒弃预先设计的anchors，在每个特征位置上直接预测物体。对于每个实例，作者将不同尺度层级上的边框内的所有位置看作为正样本或负样本。然后在训练中，作者输出正负权重图$w^{+}$和$w^{-}$来准确地调整正负样本的预测。因此，作者将整个标签分配步骤变换为2个权重图。

为了适应不同类别的分布，作者提出了类别相关、依赖于数据的加权模块，叫做中心点加权。它首先得到标准的中心点先验，然后学习每个类别的分布。

为了适应每个实例的外观和尺度，作者进一步提出了一个实例相关的加权模块，叫做置信度加权。它基于每个物体的预测置信度，动态地对空间和尺度维度的位置进行加权。

最终，作者将2个加权模块结合起来，为所有的位置产生正负权重。给定一个物体$n$，作者将其训练损失$L_n(\theta )$表示为：

$$L_n(\theta )=-\log (\sum _{i\in S_n}{\omega }_i^{+}{P}_i^{+})-\sum _{i\in S_n}\log (1-{\omega }_i^{-}{P}_i^{-})$$

其中$S_n$表示所有尺度层级上边框内所有的位置。对于位置$i\in S_n$，它是正的或负的概率表示为$P_i^{+}$和$P_i^{-}$，由该网络来预测。${\omega }_i^{+}$和${\omega }_i^{-}$是中心加权和置信度加权所产生的权重图。

3.2 中心点加权

先验分布是标签分配的一个基本元素，特别是在训练的早期阶段。通常，物体的分布服从于中心先验。但是，不同类别的物体有着不同的分布，如长颈鹿和人。继续使用中心位置采样就无法获取现实世界中不同实例的分布。对于不同类别的物体而言，自适应的中心点分布更有效。

基于中心先验，作者提出了一个带有可学习参数的、与类别相关的具有高斯形状的加权函数$G$。“与类别相关”意味着每个类别都有其独特的参数($\mu ,\sigma$)，同一类别的物体共享参数。$G$的定义是：

$$G(d|\mu ,\sigma )=e^{\frac{-(d-\mu {)}^2}{2{\sigma }^2}}$$

其中$d$表示物体内某一位置相对于其边框中心，在$x$轴和$y$轴上的偏移量，可以是负数。$\mu$和$\sigma$是形状$(K,2)$的可学习参数。$K$是一个数据集中类别的个数。每个类别有2个参数，对应着空间维度上的$x$轴和$y$轴。因为$G$会对训练损失函数做一定贡献，参数可以通过反向传播学习。

直观地，$\mu$控制每个类别的边框中心偏移量。$\sigma$基于类别的特征，计算每个位置的重要度。因此 $\sigma$ 通过合理的权重，决定多少个点可以有效地对正样本损失发挥作用。

我们也需要注意到，$G$是用于所有的FPN阶段。由于同一类别的物体有着任意的大小和宽高比，最适合的位置可能出现在任意一个FPN阶段。而且，为了弥补 FPN 不同下采样率所引起的干扰，作者通过FPN阶段的缩小比值对距离$d$做了归一化。

3.3 置信度加权

现有的动态策略设计的依据是，网络可以很容易地学习正确的样本，其置信度都较高，而对于较差的样本，它预测出的置信度都较低。特别地，置信度指示器在尺度选择（损失指示器）和空间分配（anchor置信度）中被证明很有效。在置信度加权中，作者提出了一个协同的置信度指示器，既有分类的，也有定位的，指导空间和尺度维度的加权策略。

3.3.1 分类置信度

给定一个空间位置$i$，它的分类置信度可以定义为$P_i(cls|\theta )$，目标类别的概率直接由网络预测。$\theta$表示模型的参数。但是，为了保证所有合理的位置都被考虑到，作者首先考虑了边框内的所有空间位置。由于一个物体很难完全填满一个边框，初始的正样本集合倾向于包含部分背景区域。如果某位置是背景区域，该位置所有的类别预测都是不合理的。所以将许多背景位置作为正样本会损害检测性能。

为了抑制假阳样本，作者提出了一个新的Implicit-Objectness分支，如图3所示。它和RPN或YOLO中的Objectness工作方式类似，是一个前景和背景的二元分类任务。但是这里我们有另一个问题，缺乏显式的标签。RPN和YOLO使用连续的正标签来实施预先定义的标签分配，而我们需要动态地找到并强调正样本。

因此作者一起优化了分类分支和Objectness分支，它不需要显式的标签。这也就是为什么它叫做Implicit-Objectness。对于一个位置$i\in S_n$，使用了ImpObj之后，分类置信度$P_i(cls|\theta )$的定义是：

$$P_i(cls|\theta )=P_i(cls|obj,\theta )P_i(obj|\theta )$$

其中ImpObj就是$P_i(obj|\theta )$，代表位置$i$作为前景或背景的概率。$P_i(cls|obj,\theta )$是位置$i$是某一类别的概率，假设我们知道它是前景还是背景。如图3所示，$P_i(cls|obj,\theta )$是分类输出。它和RetinaNet中的分类分支一样。

为了从另一个角度理解ImpObj，我们可以将之前的标签分配策略看作为人为选择前景，即$P_i(obj)=1$为正样本，0则是负样本。分类置信度$P_i(cls|\theta )=P_i(cls|obj,\theta )$。而在AutoAssign中，$P_i(obj|\theta )$是动态地由网络决定的。

3.3.2 联合的置信度建模

为了让每个位置的正负样本预测是公平的，除了分类，我们也应该包含定位的置信度。通常定位的输出是边框偏移量，很难直接去测算回归置信度。因此作者将定位损失$L_i^{loc}(\theta )$转换为概率$P_i(loc|\theta )$，然后将分类和回归概率结合起来，得到一个联合的置信度$P_i(\theta )$。损失$L_i(\theta )$的推演过程如下。不失一般性，这里作者使用了二元交叉熵损失来做分类。

其中$\lambda$是损失权重，平衡分类和定位。

3.3.3 加权函数

基于联合置信度$P_i(\theta )$，作者提出了指数形式的置信度加权函数$C(P_i)$，着重强调那些高置信度的位置：

$$C(P_i)=e^{\frac{P_i(\theta )}{\gamma }}$$

其中$\gamma$是调节系数，控制高置信度位置和低置信度位置对正损失的贡献大小。

3.4 权重图

3.4.1 正权重

直觉上，给定一个物体$i$，对于所有在该边框内的位置，我们应该关注那些正确的位置，它们的预测更准确。但是，在训练的一开始，网络的参数是随机初始化的，使它预测的置信度不合理。因此由先验分布的信息也很关键。对于位置$i\in S_n$，作者将中心点加权模块的类别具体的先验$G(d_i)$与置信度加权模块$C(P_i)$结合起来，产生正的权重$w_i^{+}$：

$$w_i^{+}=\frac{C(P_i)G(d_i)}{{\sum }_{j\in S_n}C(P_i)G(d_i)}$$

3.4.2 负权重

如上面讨论的，一个边框通常包含一定数量的背景位置，我们也需要加权的负损失来抑制那些位置，去除假阳样本。而且，由于边框内的位置通常倾向于预测高置信度的正样本，我们需要定位置信度来产生无偏见的假阳样本。矛盾的是，负分类对于回归任务是没有梯度的，这就意味着定位置信度不应被进一步优化。因此作者使用每个位置的预测与所有物体的IOU，来产生负权重$w_i^{-}$：

$$w_i^{-}=1-f(io{u}_i)$$

其中$f(io{u}_i)=1/(1-io{u}_i)$，$io{u}_i$表示位置$i\in S_n$与所有ground truth边框最大的IOU。为了让该权重有效，作者对$f(io{u}_i)$做了归一化，范围在$[0,1]$之间。这个变换将权重的分布更加突出，保证IOU最高的位置得到的负损失为0。对于边框外的所有点，$w_i^{-}$都设为1,因为它们肯定是背景。

3.5 损失函数

为了产生正的和负的权重图，作者动态分配更多合适的空间位置，为每个实例自动选择正确的FPN阶段。由于权重图会作用到训练损失中去，AutoAssign 以一种可微的方式来处理标签分配问题。最终的损失函数$L(\theta )$定义如下：

$$L(\theta )=-\sum _{n=1}^N\log (\sum _{i\in S_n}{w}_i^{+}{p}_i^{+})-\sum _{j\in S}\log (1-w_j^{-}{p}_j^{-})$$

其中$P^{-}=P(cls|\theta )$，$n$表示$n$个ground truth。为了确保至少有一个点能匹配到物体$n$，作者使用所有正权重的加权和，来得到最终的正置信度。$S$表示所有尺度上的所有位置。因此，对于边框内的一个点，我们就会用不同的权重来计算正负损失。这与所有其它的标签分配策略都不同。为了处理负样本定位不平衡的问题，作者使用了Focal Loss。

等式6、7中的正负权重级数不一样，正负损失的计算是独立的。