2019独角兽企业重金招聘Python工程师标准>>> ![]()
在MNIST上只有91%正确率,不太理想。在这个小节里,我们用一个稍微复杂的模型:卷积神经网络来改善效果。如果训练次数达到1万次,会达到大概99.2%的准确率,如果是1000次,则可以达到96.22%的准确率,成功率有所提高。
1、概念
1.1、神经网络。人工神经网络(Artificial Neural Networks,简写为ANNs)也简称为神经网络(Neural Networks,NN)或称作连接模型(Connection Model),神经网络是一种模拟人脑的神经网络以期能够实现类人工智能的机器学习技术。
人脑中的神经网络是一个非常复杂的组织。成人的大脑中估计有1000亿个神经元之多。
图1 人脑神经网络
那么机器学习中的神经网络是如何实现这种模拟的,并且达到一个惊人的良好效果的?
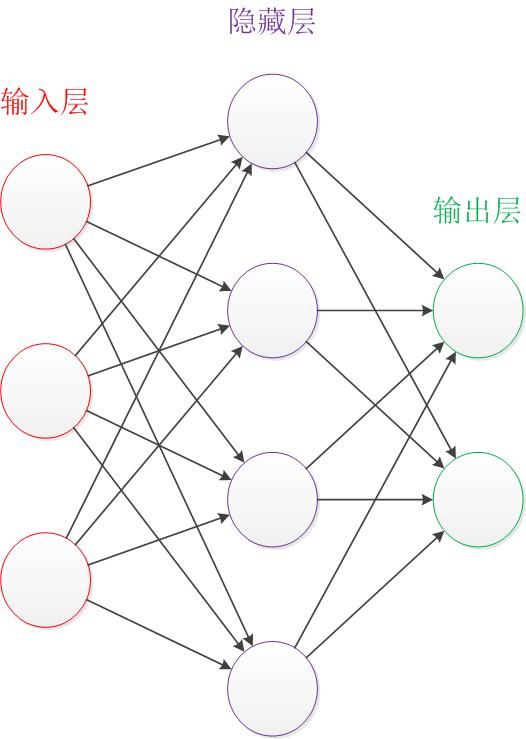
让我们来看一个经典的神经网络。这是一个包含三个层次的神经网络。红色的是输入层,绿色的是输出层,紫色的是中间层(也叫隐藏层)。输入层有3个输入单元,隐藏层有4个单元,输出层有2个单元。后文中,我们统一使用这种颜色来表达神经网络的结构。
图2 神经网络结构图
在开始介绍前,有一些知识可以先记在心里:
- 设计一个神经网络时,输入层与输出层的节点数往往是固定的,中间层则可以自由指定;
- 神经网络结构图中的拓扑与箭头代表着预测过程时数据的流向,跟训练时的数据流有一定的区别;
- 结构图里的关键不是圆圈(代表“神经元”),而是连接线(代表“神经元”之间的连接)。每个连接线对应一个不同的权重(其值称为权值),这是需要训练得到的。
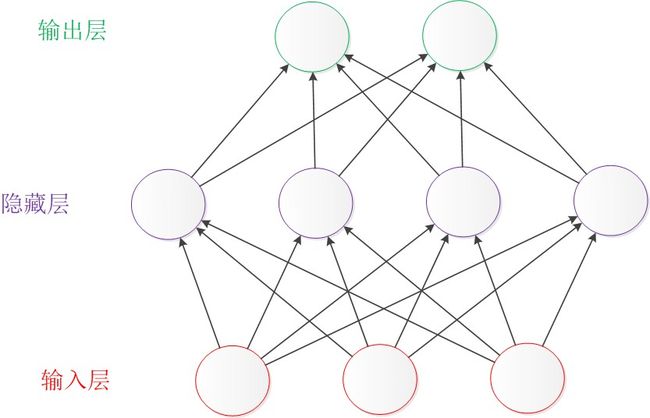
除了从左到右的形式表达的结构图,还有一种常见的表达形式是从下到上来表示一个神经网络。这时候,输入层在图的最下方。输出层则在图的最上方,如下图:
图3 从下到上的神经网络结构图
从左到右的表达形式以Andrew Ng和LeCun的文献使用较多,Caffe里使用的则是从下到上的表达。在本文中使用Andrew Ng代表的从左到右的表达形式。
下面从简单的神经元开始说起,一步一步介绍神经网络复杂结构的形成。
2. 神经元
2.1.引子
对于神经元的研究由来已久,1904年生物学家就已经知晓了神经元的组成结构。
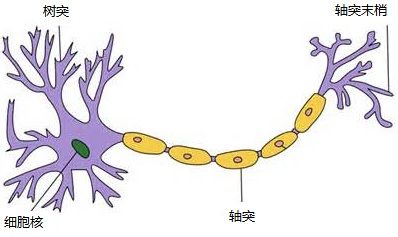
一个神经元通常具有多个树突,主要用来接受传入信息;而轴突只有一条,轴突尾端有许多轴突末梢可以给其他多个神经元传递信息。轴突末梢跟其他神经元的树突产生连接,从而传递信号。这个连接的位置在生物学上叫做“突触”。
人脑中的神经元形状可以用下图做简单的说明:
图4 神经元
2.2.结构
神经元模型是一个包含输入,输出与计算功能的模型。输入可以类比为神经元的树突,而输出可以类比为神经元的轴突,计算则可以类比为细胞核。
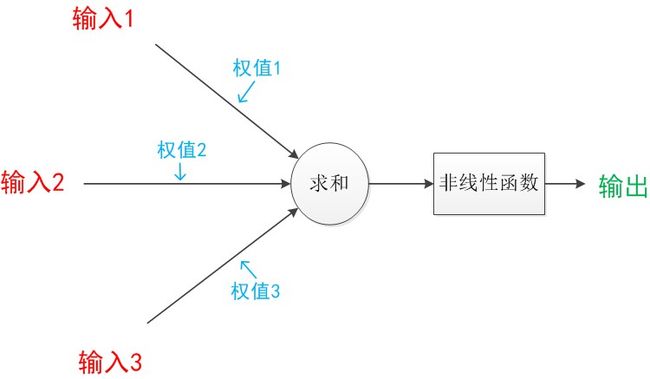
下图是一个典型的神经元模型:包含有3个输入,1个输出,以及2个计算功能。
注意中间的箭头线。这些线称为“连接”。每个连接上有一个“权值”。
图5 神经元模型
连接是神经元中最重要的东西。每一个连接上都有一个权重。
一个神经网络的训练算法就是让权重的值调整到最佳,以使得整个网络的预测效果最好。
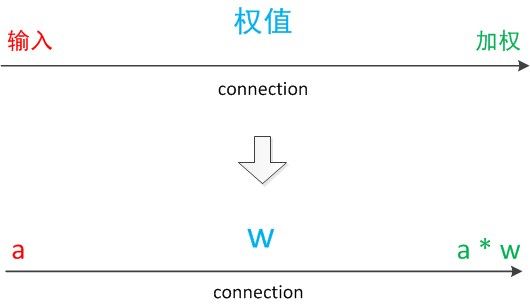
我们使用a来表示输入,用w来表示权值。一个表示连接的有向箭头可以这样理解:在初端,传递的信号大小仍然是a,端中间有加权参数w,经过这个加权后的信号会变成a*w,因此在连接的末端,信号的大小就变成了a*w。
在其他绘图模型里,有向箭头可能表示的是值的不变传递。而在神经元模型里,每个有向箭头表示的是值的加权传递。
图6 连接(connection)
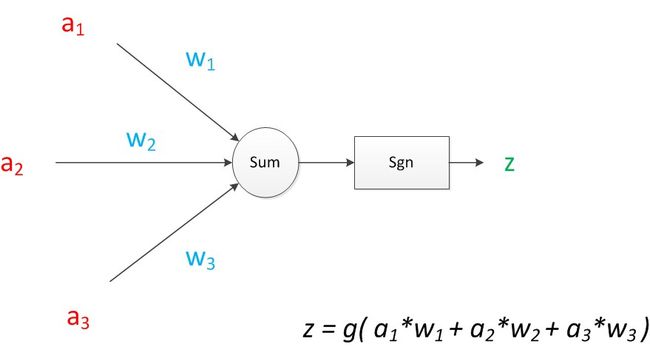
如果我们将神经元图中的所有变量用符号表示,并且写出输出的计算公式的话,就是下图。
图7 神经元计算
可见z是在输入和权值的线性加权和叠加了一个函数g的值。在MP模型里,函数g是sgn函数,也就是取符号函数。这个函数当输入大于0时,输出1,否则输出0。
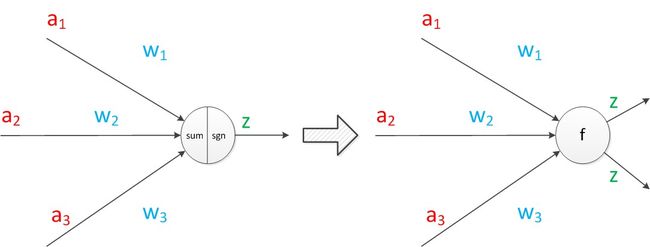
下面对神经元模型的图进行一些扩展。首先将sum函数与sgn函数合并到一个圆圈里,代表神经元的内部计算。其次,把输入a与输出z写到连接线的左上方,便于后面画复杂的网络。最后说明,一个神经元可以引出多个代表输出的有向箭头,但值都是一样的。
神经元可以看作一个计算与存储单元。计算是神经元对其的输入进行计算功能。存储是神经元会暂存计算结果,并传递到下一层。
图8 神经元扩展
当我们用“神经元”组成网络以后,描述网络中的某个“神经元”时,我们更多地会用“单元”(unit)来指代。同时由于神经网络的表现形式是一个有向图,有时也会用“节点”(node)来表达同样的意思。
2.3.效果
神经元模型的使用可以这样理解:
我们有一个数据,称之为样本。样本有四个属性,其中三个属性已知,一个属性未知。我们需要做的就是通过三个已知属性预测未知属性。
具体办法就是使用神经元的公式进行计算。三个已知属性的值是a1,a2,a3,未知属性的值是z。z可以通过公式计算出来。
这里,已知的属性称之为特征,未知的属性称之为目标。假设特征与目标之间确实是线性关系,并且我们已经得到表示这个关系的权值w1,w2,w3。那么,我们就可以通过神经元模型预测新样本的目标。
4.分类
人工神经网络模型主要考虑网络连接的拓扑结构、神经元的特征、学习规则等。目前,已有近40种神经网络模型,其中有反传网络、感知器、自组织映射、Hopfield网络、波耳兹曼机、适应谐振理论等。根据连接的拓扑结构,神经网络模型可以分为:
(1)前向网络 网络中各个神经元接受前一级的输入,并输出到下一级,网络中没有反馈,可以用一个有向无环路图表示。这种网络实现信号从输入空间到输出空间的变换,它的信息处理能力来自于简单非线性函数的多次复合。网络结构简单,易于实现。反传网络是一种典型的前向网络。
(2)反馈网络 网络内神经元间有反馈,可以用一个无向的完备图表示。这种神经网络的信息处理是状态的变换,可以用动力学系统理论处理。系统的稳定性与联想记忆功能有密切关系。Hopfield网络、波耳兹曼机均属于这种类型。
学习是神经网络研究的一个重要内容,它的适应性是通过学习实现的。根据环境的变化,对权值进行调整,改善系统的行为。由Hebb提出的Hebb学习规则为神经网络的学习算法奠定了基础。Hebb规则认为学习过程最终发生在神经元之间的突触部位,突触的联系强度随着突触前后神经元的活动而变化。在此基础上,人们提出了各种学习规则和算法,以适应不同网络模型的需要。有效的学习算法,使得神经网络能够通过连接权值的调整,构造客观世界的内在表示,形成具有特色的信息处理方法,信息存储和处理体现在网络的连接中。
5、常见神经网络
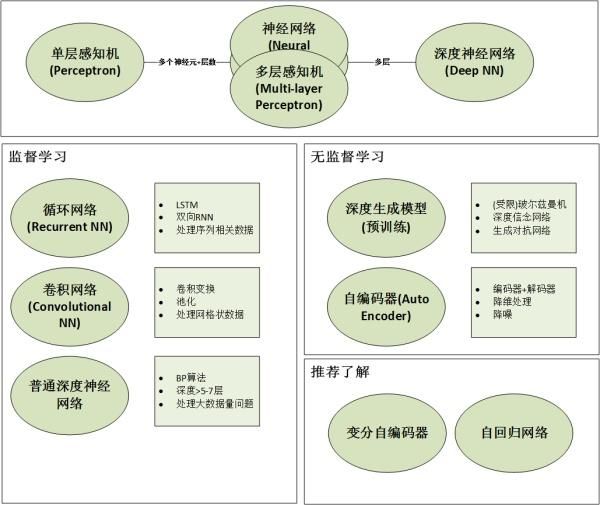
常见神经网络有很多种,下面先给大家看一张总览图:
是不是感觉有好多神经网络没见过?下面我们对主流的几种神经网络进行说明。
网络包括:
5.1、 有监督的神经网络(Supervised Neural Networks)
5.1.1、 神经网络(Artificial Neural Networks)和深度神经网络(Deep Neural Networks)
追根溯源的话,神经网络的基础模型是感知机(Perceptron),因此神经网络也可以叫做多层感知机(Multi-layer Perceptron),简称MLP。单层感知机叫做感知机,多层感知机(MLP) 人工神经网络(ANN)。
那么多层到底是几层?一般来说有1-2个隐藏层的神经网络就可以叫做多层,准确的说是(浅层)神经网络(Shallow Neural Networks)。随着隐藏层的增多,更深的神经网络(一般来说超过5层)就都叫做深度学习(DNN)。然而,“深度”只是一个商业概念,很多时候工业界把3层隐藏层也叫做“深度学习”,所以不要在层数上太较真。在机器学习领域的约定俗成是,名字中有深度(Deep)的网络仅代表其有超过5-7层的隐藏层。
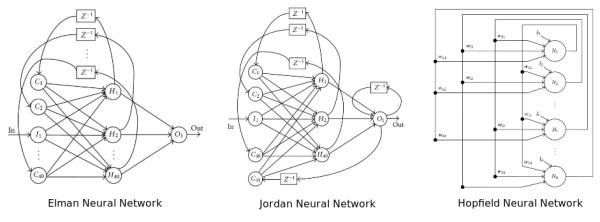
神经网络的结构指的是“神经元”之间如何连接,它可以是任意深度。以下图的3种不同结构为例,我们可以看到连接结构是非常灵活多样的。
图片来源:10 Misconceptions about Neural Networks
需要特别指出的是,卷积网络(CNN)和循环网络(RNN)一般不加Deep在名字中的原因是:它们的结构一般都较深,因此不需要特别指明深度。想对比的,自编码器(Auto Encoder)可以是很浅的网络,也可以很深。所以你会看到人们用Deep Auto Encoder来特别指明其深度。
应用场景:全连接的前馈深度神经网络(Fully Connected Feed Forward Neural Networks),也就是DNN适用于大部分分类(Classification)任务,比如数字识别等。但一般的现实场景中我们很少有那么大的数据量来支持DNN,所以纯粹的全连接网络应用性并不是很强。
5.1. 2、 循环神经网络(Recurrent Neural Networks)和递归神经网络(Recursive Neural Networks)
虽然很多时候我们把这两种网络都叫做RNN,但事实上这两种网路的结构事实上是不同的。而我们常常把两个网络放在一起的原因是:它们都可以处理有序列的问题,比如时间序列等。
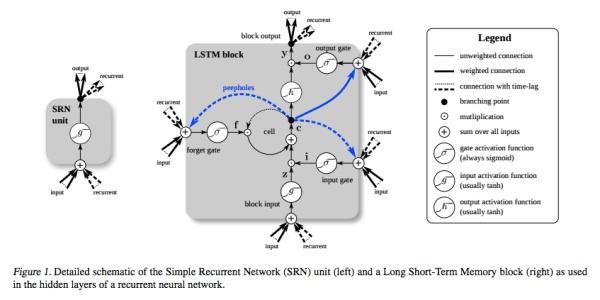
举个最简单的例子,我们预测股票走势用RNN就比普通的DNN效果要好,原因是股票走势和时间相关,今天的价格和昨天、上周、上个月都有关系。而RNN有“记忆”能力,可以“模拟”数据间的依赖关系(Dependency)。为了加强这种“记忆能力”,人们开发各种各样的变形体,如非常著名的Long Short-term Memory(LSTM),用于解决“长期及远距离的依赖关系”。如下图所示,左边的小图是最简单版本的循环网络,而右边是人们为了增强记忆能力而开发的LSTM。
同理,另一个循环网络的变种 – 双向循环网络(Bi-directional RNN)也是现阶段自然语言处理和语音分析中的重要模型。开发双向循环网络的原因是语言/语音的构成取决于上下文,即“现在”依托于“过去”和“未来”。单向的循环网络仅着重于从“过去”推出“现在”,而无法对“未来”的依赖性有效的建模。
递归神经网络和循环神经网络不同,它的计算图结构是树状结构而不是网状结构。递归循环网络的目标和循环网络相似,也是希望解决数据之间的长期依赖问题。而且其比较好的特点是用树状可以降低序列的长度,熟悉数据结构的朋友都不陌生。但和其他树状数据结构一样,如何构造最佳的树状结构如平衡树/平衡二叉树并不容易。
应用场景:语音分析,文字分析,时间序列分析。主要的重点就是数据之间存在前后依赖关系,有序列关系。一般首选LSTM,如果预测对象同时取决于过去和未来,可以选择双向结构,如双向LSTM。
5.1.3、 卷积网络(Convolutional Neural Networks)
卷积网络早已大名鼎鼎,从某种意义上也是为深度学习打下良好口碑的功臣。不仅如此,卷积网络也是一个很好的计算机科学借鉴神经科学的例子。卷积网络的精髓其实就是在多个空间位置上共享参数,据说我们的视觉系统也有相类似的模式。
首先简单说什么是卷积。卷积运算是一种数学计算,和矩阵相乘不同,卷积运算可以实现稀疏相乘和参数共享,可以压缩输入端的维度。和普通DNN不同,CNN并不需要为每一个神经元所对应的每一个输入数据提供单独的权重。与池化(pooling)相结合,CNN可以被理解为一种公共特征的提取过程,不仅是CNN大部分神经网络都可以近似的认为大部分神经元都被用于特征提取。
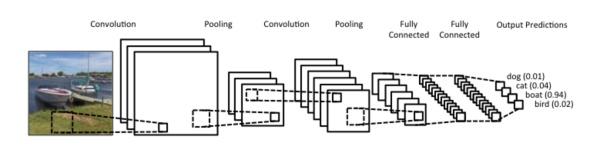
以上图为例,卷积、池化的过程将一张图片的维度进行了压缩。从图示上我们不难看出卷积网络的精髓就是适合处理结构化数据,而该数据在跨区域上依然有关联。
应用场景:虽然我们一般都把CNN和图片联系在一起,但事实上CNN可以处理大部分格状结构化数据(Grid-like Data)。举个例子,图片的像素是二维的格状数据,时间序列在等时间上抽取相当于一维的的格状数据,而视频数据可以理解为对应视频帧宽度、高度、时间的三维数据。
5.2、 无监督的预训练网络(Unsupervised Pre-trained Neural Networks)
5.2.1、 深度生成模型(Deep Generative Models)
说到生成模型,大家一般想到的无监督学习中的很多建模方法,比如拟合一个高斯混合模型或者使用贝叶斯模型。深度学习中的生成模型主要还是集中于想使用无监督学习来帮助监督学习,毕竟监督学习所需的标签代价往往很高…所以请大家不要较真我把这些方法放在了无监督学习中。
5.2.1.1、 玻尔兹曼机(Boltzmann Machines)和受限玻尔兹曼机(Restricted Boltzmann Machines)
每次一提到玻尔兹曼机和受限玻尔兹曼机我其实都很头疼。简单的说,玻尔兹曼机是一个很漂亮的基于能量的模型,一般用最大似然法进行学习,而且还符合Hebb’s Rule这个生物规律。但更多的是适合理论推演,有相当多的实际操作难度。
而受限玻尔兹曼机更加实际,它限定了其结构必须是二分图(Biparitite Graph)且隐藏层和可观测层之间不可以相连接。此处提及RBM的原因是因为它是深度信念网络的构成要素之一。
应用场景:实际工作中一般不推荐单独使用RBM…
5.2.1.2、 深度信念网络(Deep Belief Neural Networks)
DBN是祖师爷Hinton在06年提出的,主要有两个部分: 1. 堆叠的受限玻尔兹曼机(Stacked RBM) 2. 一层普通的前馈网络。
DBN最主要的特色可以理解为两阶段学习,阶段1用堆叠的RBM通过无监督学习进行预训练(Pre-train),阶段2用普通的前馈网络进行微调。就像我上文提到的,神经网络的精髓就是进行特征提取。和后文将提到的自动编码器相似,我们期待堆叠的RBF有数据重建能力,及输入一些数据经过RBF我们还可以重建这些数据,这代表我们学到了这些数据的重要特征。
将RBF堆叠的原因就是将底层RBF学到的特征逐渐传递的上层的RBF上,逐渐抽取复杂的特征。比如下图从左到右就可以是低层RBF学到的特征到高层RBF学到的复杂特征。在得到这些良好的特征后就可以用第二部分的传统神经网络进行学习。
多说一句,特征抽取并重建的过程不仅可以用堆叠的RBM,也可以用后文介绍的自编码器。
应用场景:现在来说DBN更多是了解深度学习“哲学”和“思维模式”的一个手段,在实际应用中还是推荐CNN/RNN等,类似的深度玻尔兹曼机也有类似的特性但工业界使用较少。
5.2.1.3. 生成式对抗网络(Generative Adversarial Networks)
生成式对抗网络用无监督学习同时训练两个模型,内核哲学取自于博弈论…
简单的说,GAN训练两个网络:1. 生成网络用于生成图片使其与训练数据相似 2. 判别式网络用于判断生成网络中得到的图片是否是真的是训练数据还是伪装的数据。生成网络一般有逆卷积层(deconvolutional layer)而判别网络一般就是上文介绍的CNN。
熟悉博弈论的朋友都知道零和游戏(zero-sum game)会很难得到优化方程,或很难优化,GAN也不可避免这个问题。但有趣的是,GAN的实际表现比我们预期的要好,而且所需的参数也远远按照正常方法训练神经网络,可以更加有效率的学到数据的分布。
另一个常常被放在GAN一起讨论的模型叫做变分自编码器(Variational Auto-encoder),有兴趣的读者可以自己搜索。
应用场景:现阶段的GAN还主要是在图像领域比较流行,但很多人都认为它有很大的潜力大规模推广到声音、视频领域。
5.2.2. 自编码器(Auto-encoder)
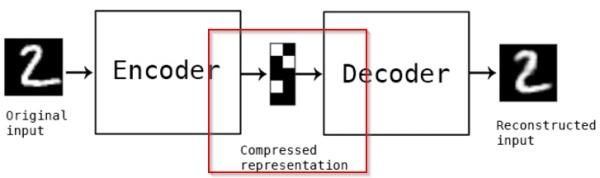
自编码器是一种从名字上完全看不出和神经网络有什么关系的无监督神经网络,而且从名字上看也很难猜测其作用。让我们看一幅图了解它的工作原理…
如上图所示,Autoencoder主要有2个部分:1. 编码器(Encoder) 2. 解码器(Decoder)。我们将输入(图片2)从左端输入后,经过了编码器和解码器,我们得到了输出….一个2。但事实上我们真正学习到是中间的用红色标注的部分,即数在低维度的压缩表示。评估自编码器的方法是重建误差,即输出的那个数字2和原始输入的数字2之间的差别,当然越小越好。
和主成分分析(PCA)类似,自编码器也可以用来进行数据压缩(Data Compression),从原始数据中提取最重要的特征。认真的读者应该已经发现输入的那个数字2和输出的数字2略有不同,这是因为数据压缩中的损失,非常正常。
应用场景:主要用于降维(Dimension Reduction),这点和PCA比较类似。同时也有专门用于去除噪音还原原始数据的去噪编码器(Denoising Auto-encoder)。
2、卷积神经网络
卷积神经网络(Convolutional Neural Network,CNN)是一种前馈神经网络(前馈神经网络是一种最简单的神经网络,各神经元分层排列。每个神经元只与前一层的神经元相连。接收前一层的输出,并输出给下一层.各层间没有反馈。是目前应用最广泛、发展最迅速的人工神经网络之一。),它的人工神经元可以响应一部分覆盖范围内的周围单元,对于大型图像处理有出色表现。 它包括卷积层(convolutional layer)和池化层(pooling layer)。
2.1 卷积
从数学上讲,卷积就是一种运算。
某种运算,能被定义出来,至少有以下特征:
- 首先是抽象的、符号化的
- 其次,在生活、科研中,有着广泛的作用
比如加法:
- 是抽象的,本身只是一个数学符号
- 在现实中,有非常多的意义,比如增加、合成、旋转等等
卷积,是我们学习高等数学之后,新接触的一种运算,因为涉及到积分、级数,所以看起来觉得很复杂。
2.2 卷积的知识
卷积的数学定义大家都可以在网络上搜索到。我就不在这里进行复述。在这里主要进行卷积的通俗理解的讲解。
卷积本身不过就是一种数学运算而已。它就是一种各种元素相乘累加的极限形式。
卷积的物理含义就是:当前的输出不但同当前的输入有关,还与以前的所有输入有关。但是,也不能说当前的输入和以前的输入都同等重要啊,所以,不同的输入的权重是不同的,也就是说,卷积就是不同的输入信号的加权叠加。
对于线性系统,如果知道该系统的单位响应,那么将单位响应和输入信号求卷积,就相当于把输入信号的各个时间点的单位响应加权叠加,就直接得到了输出信号。
你可以把卷积想象成一种混合信息的手段。想象一下装满信息的两个桶,我们把它们倒入一个桶中并且通过某种规则搅拌搅拌。也就是说卷积是一种混合两种信息的流程。