【JZOJ 4623】搬运干草捆
Description
Solution
题解说用splay来解,我不会,我用贪心,
显然的,在使当前答案最优的同时,也要保证当前做到的最后一个干草的高度最高,
把每个修改后高度一样的干草合成一个块,设每个干草原高度为 ai ,修改后的整块的高度为 bk 。
我们先来考虑局部的解:
当前做到i,
如果 bk=ai ,直接合并上去,
如果 bk>ai ,新开一个块,
如果 bk<ai ,分类讨论:
设块中(含新加的i)的 a⩽bk 有x个, a>bk 有y个,
一个结论:在只有两个点的情况下,把一个点升高和把另一个点减低的代价是一样的,
同样的,如果块中 x=y ,那么结论同样成立,因为我们可以把它们看成一高一低两两配对的点对。
当 x>y 时,只能把i点降低,
当 x=y 时,代价与上情况相同,因为代价不变,可以升高整块的高度,
找到一个高度 q=minaj>bk{aj} (用主席树)为升高的上限高度,因为如果再升高代价就会变,
如果q大于上一个块的高度 bk−1 ,显然不合法,只把当前区间升到 bk−1 ,并把这两个块合并,
如果不是,就直接上升到q,
最后的答案就是每个块的代价和,
复杂度: O(nlog(n))
图片from YxuanwKeith

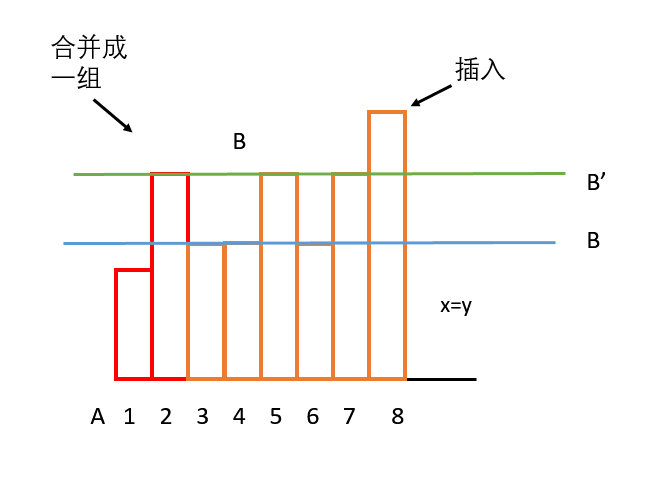
Code
#includereturn find(t+1,r,b[e1].r,b[e2].r,l1);
else
{
wwq s=find(l,t,b[e1].l,b[e2].l,l1);
if(s.s)return s;
return find(t+1,r,b[e1].r,b[e2].r,l1);
}
}
int main()
{
int mx=0;
wwq q;
read(n);
fo(i,1,n)mx=max(mx,read(a[i]));
za[0].b=INF;
fo(i,1,n)
{
build(1,mx,root[i-1],root[i],a[i]);
if(za[za0].b>a[i])za[++za0].x=1,za[za0].y=0,za[za0].b=a[i],za[za0].ans=0,za[za0].i=i;
else if(za[za0].b==a[i])za[za0].x++;
else
{
za[za0].y++;za[za0].ans+=a[i]-za[za0].b;
while(za[za0].x==za[za0].y)
{
q=find(1,mx,root[za[za0].i-1],root[i],za[za0].b+1);
if(q.ans<=za[za0-1].b)za[za0].x+=q.s,za[za0].y-=q.s,za[za0].b=q.ans;
if(q.ans>=za[za0-1].b)
{
za[za0-1].x+=za[za0].x;
za[za0-1].y+=za[za0].y;
za[za0-1].ans+=za[za0].ans;
za0--;
}
}
}
}
ans=0;
fo(i,1,za0)ans+=za[i].ans;
printf("%lld\n",ans);
return 0;
} 