树状数组

转载自：点击打开链接  感谢作者

代码部分前 的讲解主要 基于 线段树单点更新，区间查询  后面的为算法变形延伸

树状数组，又称二进制索引树，英文名Binary Indexed Tree。

一、树状数组的用途

主要用来求解数列的前缀和，a[0]+a[1]+...+a[n]。

由此引申出三类比较常见问题：

1、单点更新，区间求值。（HDU1166）

2、区间更新，单点求值。（HDU1556）

3、求逆序对。（HDU2838）

 

二、树状数组的表示

1、公式表示

设A[]为一个已知的数列。C[]为树状数组。则会有

C[i]=A[j]+...+A[i]；而且有个有趣的性质，设节点编号为i，那么这个节点管辖的区间为2^k（其中k为x二进制末尾0的个数）个元素

具体算这个2^k有一个快捷的办法：x & (-x)  或者 x & (x ^ (x - 1) )

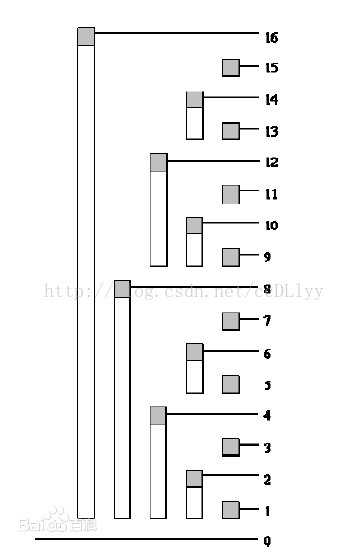
2、图形表示

（注：最下面的一行表示数组A，上面的二进制表示的部分是C）

从以上可以发现：

1、树状数组C是表示普通数组A的一部分的和。

2、小标为奇数时，C[i]只能管辖一个A[i]。

3、C[i]的最后一个数一定是A[i]。

树状数组的充分性：

很容易知道C8表示A1～A8的和，但是C6却是表示A5～A6的和，为什么会产生这样的区别的呢？或者说发明她的人为什么这样区别对待呢？答案是，这样会使操作更简单！看到这相信有些人就有些感觉了，为什么复杂度被log了呢？可以看到，C8可以看作A1～A8的左半边和+右半边和，而其中左半边和是确定的C4，右半边其实也是同样的规则把A5～A8一分为二……继续下去都是一分为二直到不能分树状数组巧妙地利用了二分，树状数组并不神秘，关键是巧妙！

三、树状数组的关键代码

1、

 int lowBit(int x)
 {
     return x&(-x);
 }

这段代码可以简单的理解为是树状数组向前或向后衍生是用的。

向后主要是为了找到目前节点的父节点，比如要将C[4]+1，那么4+(4&(-4))=8，C[8]+1，8+(8&(-8))=16，

C[16]+1。

向前主要是为了求前缀和，比如要求A[1]+...+A[12]。那么，C[12]=A[9]+...+A[12]；然后12-12&(-12)=8，

C[8]=A[1]+...+A[8]。

 

2、

 void modify(int pos,int num)  //pos为数组下标位置，num为要增加的值
 {
     while(pos<=n)   //n为数组的长度
     {
         c[pos]+=num;
         pos+=lowBit(pos);
     }
 }

这段代码是用来更新树状数组的，包括区间更新、单点更新。

就是想刚才所说的，一点更新了，要不断将父节点也更新。

 

3、

 int getResult(int pos)  //求A[1]+...+A[pos]
 {
     int sum=0;
     while(pos>0)
     {
         sum+=c[pos];
         pos-=lowBit(pos);
     }

     return sum;
 }

这段代码用来求解前缀和的。

就像刚才说的，求解A[1]+...+A[12]，也就是C[12]+C[8]搞定。

 

四、树状数组的优点

1、原本的长度为n的数列求和时间复杂度为O(n)，更改的时间复杂度为O(1)。

树状数组将复杂度优化为O(logn)。在n较大时，效率更高。

2、树状数组编码简单。

3、树状数组是一个可以很高效的进行区间统计的数据结构。在思想上类似于线段树，空间复杂度略低，比线段树节省空间，编程复杂度比线段树低，但适用范围比线段树小，对可以进行的运算也有限制，比如每次要查询的是一个区间的最小值，似乎就没有很好的解决办法。

 

五、注意

1、树状数组的下标要从1开始。

2、pos-pos&(-pos)就到了下一个无联系的节点很容易理解。

为什么pos+pos&(-pos)就得到pos的父节点？这个根据 图 和 上面证明树状数组充分性的二分思想容易看出。

对于玄玄的东西，自己非要去搞复杂的数学证明，反而会扰了心智，如果不是数学家和算法工程师，大致知道如何得到的即可，对于大多数人，关键还是熟练运用算法。

 六、拓展

1、有的题目为改变的是一个区间，查询的反而是一个点，即区间更新，单点查询，表面上看，似乎和树状数组的使用方法恰好相反，实际上可以通过一个转化巧妙的解决。

首先对于每个数A定义集合up(A)表示{A, A+lowestbit(A), A+lowestbit(A)+lowestbit(A+lowestbit(A))...} 定义集合down(A)表示{A, A-lowestbit(A), A-lowestbit(A)-lowestbit(A-lowestbit(A)) ... , 0}。可以发现对于任何A如果更新up(A，data)和up(B+1,-data)，查询down(C)就能达到要求。

2、无论单点更新、区间查询还是区间更新、单点查询，树状数组均能应用于多维的情况。

七、代码：

HDU1166

单点更新，区间求值

 using namespace std;

 const int maxn=50001;

 int a[maxn];
 int c[maxn];
 int n;

 int lowBit(int t)
 {
     return t&(-t);
 }

 void modify(int t,int num)
 {
     while(t<=n)
     {
         c[t]+=num;
         t+=lowBit(t);
     }
 }

 int getResult(int t)
 {
     int num=0;
     while(t>0)
     {
         num+=c[t];
         t-=lowBit(t);
     }

     return num;
 }

 void init()
 {
     for(int i=1;i<=n;i++)
     {
         scanf("%d",&a[i]);

         modify(i,a[i]);
     }
 }


 int main()
 {
     int cas,Case=1;

     scanf("%d",&cas);
     while(cas--)
     {
         memset(c,0,sizeof(c));
         printf("Case %d:\n",Case++);

         scanf("%d",&n);

         init();

         char ch[15];
         int a,b;
         while(scanf("%s",&ch),strcmp(ch,"End"))
         {
             scanf("%d%d",&a,&b);

             switch(ch[0])
             {
                 case 'Q':
                     printf("%d\n",getResult(b)-getResult(a-1));
                     break;
                 case 'A':
                     modify(a,b);
                     break;
                 case 'S':
                     modify(a,-b);
                     break;
             }
          }
      }

      system("pause");
      return 0;
 }

 

HDU1556

区间更新，单点求值

 #include
 using namespace std;

 const int maxn=100001;

 int c[maxn];
 int n;

 int lowbit(int t)
 {
     return t&(-t);
 }

 void insert(int t,int d)
 {
     while(t<=n)
     {
         c[t]+=d;
         t+=lowbit(t);
     }
 }

 int getSum(int t)
 {
     int sum=0;
     while(t>0)
     {
         sum+=c[t];
         t-=lowbit(t);
     }

     return sum;
 }

 int main()
 {
     while(cin>>n,n)
     {
         int a,b;
         memset(c,0,sizeof(c));

         for(int i=1;i<=n;i++)
         {
             scanf("%d%d",&a,&b);

             insert(a,1);
             insert(b+1,-1);
         }

        for(int j=1;j
        {
             printf("%d ",getSum(j));
        }
        printf("%d\n",getSum(n));
     }

     system("pause");
     return 0;
 }

 

HDU2838

求逆序对

 #include
 using namespace std;

 const int maxn=100001;

 struct node
 {
     int cnt;
     __int64 sum;
 }tree[maxn];

 int n;

 int lowBit(int x)
 {
     return x&(-x);
 }

 void modify(int x,int y,int t)
 {
     while(x<=n)
     {
         tree[x].sum+=y;
         tree[x].cnt+=t;  //tree[].cnt来保存是否出现过a
         x+=lowBit(x);
     }
 }

 __int64 query_cnt(int x)   //比x小的数的个数
 {
     __int64 sum=0;
     while(x>0)
     {
         sum+=tree[x].cnt;
         x-=lowBit(x);
     }

     return sum;
 }

 __int64 query_sum(int x)  //比x小的所有数之和
 {
     __int64 sum=0;
     while(x>0)
     {
         sum+=tree[x].sum;
         x-=lowBit(x);
     }

     return sum;
 }

 int main()
 {
     while(~scanf("%d",&n))
     {
         int a;
         __int64 ans=0;
         memset(tree,0,sizeof(tree));

         for(int i=1;i<=n;i++)
         {
             scanf("%d",&a);

             modify(a,a,1);  //以a为下标更新数组

             __int64 k1=i-query_cnt(a);   //k1为前i个数比a大的数的个数
             if(k1!=0)
             {
                 __int64 k2=query_sum(n)-query_sum(a); //目前所有数的和-目前所有比a小的数的和，为比a大的数的和
                 ans+=k1*a+k2;   //调换a所需的时间
             }
         }

         printf("%I64d\n",ans);
     }

     system("pause");
     return 0;
 }

 另一个题解：

分析：其实这个结果和逆序数有关，对某个位置i，如果前面比他大的有x个，那么a[i]至少要加x次 
如果后面有y个比a[i]小，那么a[i]至少要加y次，也就是说用两个树状数组来分别维护当前位置时前面有多少比他大，后面有多少个比他小

#include 
#include 
#include 
using namespace std;

#define N 100001
#define ll long long

ll C[N],B[N];
ll num[N];
int T;

int Lowbit(int x){
    return x&(x^(x-1));
}

void add(ll C[],ll pos,ll num) {
    while(pos <= N) {//x最大是N
        C[pos] += num;
        pos += Lowbit(pos);
    }
}

ll Sum(ll C[],ll end) {
    ll sum = 0;
    while(end > 0) {
        sum += C[end];
        end -= Lowbit(end);
    }
    return sum;
}

int main() {
    int s, t, i, j, T;
    ll ans;
    while(~scanf("%d",&T)) {
        memset(C,0,sizeof(C));
        memset(B,0,sizeof(B));

        memset(num,0,sizeof(num));
        ans = 0;
        for(i = 1; i <= T; i ++) {
            scanf("%I64d",&num[i]);
            add(C,num[i],1);
            ans += num[i] *(i - Sum(C,num[i])) ;//计算当前点前面大于它的数的个数
        }
        for(i = T; i > 0; --i){//注意是从T至0的，
            ans += num[i] * Sum(B,num[i] - 1);//计算当前点后面小于它的个数
            add(B,num[i],1);//从后面算起，然后加起来，那么Sum求出来的就是它后面小于它的个数了
        }
        printf("%I64d\n",ans);

    }
    return 0;
}

八、二维树状数组

C[x][y]=sum(A[i][j])。其中，x-lowBit(x)+1<=i<=x，y-lowBit(y)+1<=j<=y。

例题：HDU1892

二维树状数组一般就是对矩阵的操作，更新、求值

代码：

 #include
 using namespace std;

 const int maxn=1005;

 int c[maxn][maxn];

 int lowBit(int x)
 {
     return x&(-x);
 }

 void modify(int x,int y,int val)
 {
     for(int i=x;i
     {
         for(int j=y;j
         {
             c[i][j]+=val;
         }
     }
 }

 int getResult(int x,int y)
 {
     int sum=0;
     for(int i=x;i>0;i-=lowBit(i))
     {
         for(int j=y;j>0;j-=lowBit(j))
         {
             sum+=c[i][j];
         }
     }

     return sum;
 }

 int getVal(int x,int y)
 {
     return getResult(x,y)-getResult(x-1,y)-getResult(x,y-1)+getResult(x-1,y-1);
 }

 void init()
 {
     memset(c,0,sizeof(c));

     for(int i=1;i
     {
         for(int j=1;j
         {
             modify(i,j,1);
         }
     }
 }

 int main()
 {
     int cas,cas1=1,query;

     scanf("%d",&cas);
     while(cas--)
     {
         init();

         scanf("%d",&query);

         printf("Case %d:\n",cas1++);
         for(int i=1;i<=query;i++)
         {
             char ch;
             int x1,y1,x2,y2,n;

             getchar();
             scanf("%c",&ch);

             switch(ch)
             {
                 case 'S':
                     {
                     scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
                     int x11=min(x1,x2);
                     int x22=max(x1,x2);
                     int y11=min(y1,y2);
                     int y22=max(y1,y2);
                     printf("%d\n",getResult(x22+1,y22+1)-getResult(x11,y22+1)-getResult(x22+1,y11)+getResult(x11,y11));
                     break;
                     }
                 case 'A':
                     {
                     scanf("%d%d%d",&x1,&y1,&n);
                     modify(x1+1,y1+1,n);
                     break;
                     }
                 case 'M':
                     {
                     scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&n);
                     int v=getVal(x1+1,y1+1);
                     int Min=min(n,v);
                     modify(x1+1,y1+1,-Min);
                     modify(x2+1,y2+1,Min);
                     break;
                     }
                 case 'D':
                     {
                     scanf("%d%d%d",&x1,&y1,&n);
                     int v=getVal(x1+1,y1+1);
                     int Min=min(v,n);
                     modify(x1+1,y1+1,-Min);
                     break;
                     }
             }
         }
     }

     system("pause");
     return 0;
 }

 

九、参考文章
http://mindlee.net/2011/07/10/binary-indexed-trees/ 

http://dongxicheng.org/structure/binary_indexed_tree/