关于图像处理——运用CNN实现数字手写体识别的调研

关于图像处理——运用CNN实现数字手写体识别的调研

电子科技大学 格拉斯哥学院 2017级 余尔聪

前言

关于图像处理

当下的21世纪是一个充满信息的时代，图像作为人类感知世界的视觉基础，是人类获取信息、表达信息和传递信息的重要手段。数字图像处理技术，即用计算机对图像进行处理的技术，在当下被广泛地运用到医学，教育，军事等多个领域。受学校以图像处理为主题的新生研讨课的启发，在参加完深度学习课程后，希望通过此例对图像识别有更深入的了解。

关于CNN

卷积神经网络（Convolutional Neural Networks,CNN）是一类包含卷积或相关计算且具有深度结构的前馈神经网络（Feedforward Neural Networks），是深度学习（deep learning）的代表算法之一 。由于卷积神经网络能够进行平移不变分类（shift-invariant classification），因此在文献中也被称为“平移不变人工神经网络（Shift-Invariant Artificial Neural Networks, SIANN）” 。
对卷积神经网络的研究始于二十世纪80至90年代，时间延迟网络和LeNet-5是最早被证实有效的卷积神经网络算法；在二十一世纪后，随着数值计算设备的改进，卷积神经网络得到了快速发展，并被大量应用于计算机视觉、自然语言处理等领域 。
FROM 百度百科-卷积神经网络

本例将以CNN的学习规则为基础结合BP算法，参考数据库中的原始MNIST数据，实现简单的数字手写体的识别。

正文

程序架构

以CNN为基础的程序框架主要分为特征提取（Feature Extractor）和分类器（Multi-classifier）两个部分。通过训练数据的前向（Forward Algorithm）输入运算和误差的后向传播（BP Algorithm）运算，多轮训练获得合适的权值，使得输出逐步靠近真实输出。

数据处理

• 训练数据用0-1编码，以便进行矩阵运算。本例中单个输入样本为28×28矩阵。
• 输出结果采用单热编码（e.g. ‘1’=[1 0 0 0 0 0 0 0 0 0]，仅用于分类区分），以便于网络设计与统计。

特征提取（Feature Extractor）

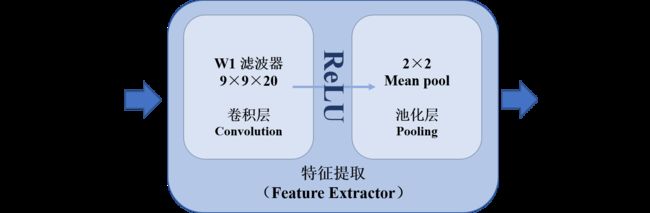
这一部分分为卷积层和池化层两部分。通过设置滤波器，我们用卷积层提取图像中的特征。（值得注意的是，用大量数据训练提取出的图像特征大部分十分抽象而与人类肉眼判断的相差很大。）随后通过池化层池化降维以便于之后的运算（本例运用取平均值的方法降维）。

• 卷积层设计

  卷积层采用20个9×9的滤波器，滤波结果选取valid部分。其后运用ReLU作为激活函数，传入池化层。

• 池化层设计

  池化层输入为20个20×20的矩阵。本例池化层采用2×2平均池化，即每四个输出为一个单元，取这四个数的均值为新的输出。最后的池化结果为20个10×10的矩阵。

分类器（Multi-classifier）

这一部分的程序设计采用包含一个有100个节点的单隐层神经网络结构（输入层+隐层+输出层）。基于梯度下降算法和BP算法，用每一个输入调整层与层之间的权重矩阵达到训练网络的目的。

• 输入层设计

1. 从特征提取网络传入的单组样本为20个10×10的矩阵（因为有20个滤波器，故而每一个输入样本有20组输出），为方便之后的分类训练，我们将其转化为一个2000×1的向量；
2. 设置第一层权重矩阵大小为100×2000；
3. 运用ReLU作为第一层的激活函数。

• 隐层设计

1. 设置隐层权重矩阵大小为10×100；
2. 设置激活函数为ReLU。

• 输出层设计

1. 设置输出层激活函数为Softmax（用于多分类问题的激活函数）；
2. 最终输出结果为10×1的向量，最大值对应表征为1，其余值表征为0。

后向传播的实现（Backward）

本例中，采用后向传播算法不断更新权值，使得最终输出逐步逼近真实值。而后后向传播的关键在于梯度下降的概念，通过从后往前传导误差，达到训练目的，在此不做赘述。
可参照公式：

（说明：J为代价函数；w为权重矩阵；e为误差；x为前层输出）

算法实现

主程序部分

% this is my main program for MNIST
% CNN and BP are used to build whole structure
% this is a basic one
% name: 余尔聪
% date: 2018-11-28

load('MNISTData.mat'); 
% import TRAINING and TESTING Data

% initiation of variables
X = X_Train; % training data-input
D = D_Train; % training data-output
W1 = randn(9,9,20); % 9×9 Convolution Matrix
W3 = (2*rand(100,2000)-1)/20; % 1st layer Weight Matrix 
W4 = (2*rand(10,100)-1)/10; % 2nd layer Weight Matrix

% Training for 1 time
    [W1,W3,W4] = CNN(X,D,W1,W3,W4);

% Show Accuracy
acc = ACC(D_Test,X_Test,W1,W3,W4);
fprintf('Accuracy is %f\n', acc);

本例只进行了一轮训练作为示例（也因为样本量足够大-60000个，但实际情况下多数需要多轮训练）。

CNN-训练部分

function [W1,W3,W4] = CNN(X,D,W1,W3,W4)
% this is the training function
% comprised of Feature Extractor and Multi-classifier
% inputs include Training input and output, W1, W2, W3
% aims to find proper W1, W2, W3 as output

    dW1 = zeros(9,9,20); % preallocating for being faster
    alpha = 0.01; % step length
    for k = 1:60000 % one epoch for one sample
        x = X(:,:,k); % initiate one epoch input
        d = D(:,k); % initiate one epoch output

前向传播（Forward）

• 特征提取（Feature Extractor）

        % Forward Algorithm
        
        % Feature Extractor 
        % comprised of Convolution and Pooling
        for m = 1:20
            V1(:,:,m) = conv2(x,rot90(W1(:,:,m),2),'valid'); % Convolution Algorithm
        end
        Y1 = max(0,V1); % Activation Function-ReLU
        Y2 = (Y1(1:2:end,1:2:end,:)+Y1(2:2:end,1:2:end,:)+Y1(1:2:end,2:2:end,:)+Y1(2:2:end,2:2:end,:))/4; 
        % Pooling by 2×2 Mean

• 分类器（Multi-classifier）

        % Multi-classifier
        y2 = reshape(Y2,[],1); % reshape Y2 into 2000×1 vector
        v3 = W3*y2; % 1st layer calculation
        y3 = max(0,v3); % ReLU
        v = W4*y3; % 2nd layer calculation
        y = Softmax(v); % Softmax-multiclassification

后向传播（Backward）

• 分类器（Multi-classifier）

        % BP Algorithm
        % Multi-classifier
        e = d-y; % error of output
        delta = e; % cross_entropy+Softmax
        e3 = W4'*delta; % error of 2nd layer
        delta3 = (v3>0).*e3; % ReLU
        e2 = W3'*delta3; % error of 1st layer

        dW4 = alpha*delta*y3'; % change in W4
        dW3 = alpha*delta3*y2'; % change in W3

        W3 = dW3+W3; % update W3
        W4 = dW4+W4; % update W4

• 特征提取（Feature Extractor）

        % Feature Extractor
        E2 = reshape(e2,size(Y2)); % reshape e2 into 10×10×20 matrix
        E1 = zeros(size(Y1));E2_4 = E2/4; % backward pooling
        E1(1:2:end,1:2:end,:) = E2_4;
        E1(1:2:end,2:2:end,:) = E2_4;
        E1(2:2:end,1:2:end,:) = E2_4;
        E1(2:2:end,2:2:end,:) = E2_4;
        delta1 = (V1>0).*E1; % ReLU
        for m = 1:20
            dW1(:,:,m) = alpha*conv2(x,rot90(delta1(:,:,m),2),'valid');
            % change in W1
        end
        W1 = W1+dW1; % update W1

结果检测

运用测试集（除训练集以外的样本）检测训练结果（三个权重矩阵）。

function acc = ACC(D_Test,X_Test,W1,W3,W4)
% This is Used to Show Accuracy
    N = length(D_Test);
    d_comp = zeros(1,N);
    for k = 1:N
        x = X_Test(:,:,k); % initiate one epoch input
        % Feature Extractor 
        % comprised of Convolution and Pooling
        for m = 1:20
            V1(:,:,m) = conv2(x,rot90(W1(:,:,m),2),'valid'); % Convolution Algorithm
        end
        Y1 = max(0,V1); % Activation Function-ReLU
        Y2 = (Y1(1:2:end,1:2:end,:)+Y1(2:2:end,1:2:end,:)+Y1(1:2:end,2:2:end,:)+Y1(2:2:end,2:2:end,:))/4; 
        % Pooling by 2×2 Average
        
        % Multi-classifier
        y2 = reshape(Y2,[],1); % reshape Y2 into 2000×1 vector
        v3 = W3*y2; % 1st layer calculation
        y3 = max(0,v3); % ReLU
        v = W4*y3; % 2nd layer calculation
        y = Softmax(v); % Softmax-multiclassification
        
        % Statistics Accuracy
        [~, i] = max(y);
        d_comp(k) = i;
    end
[~, d_true] = max(D_Test); % real output
correctMsk = (d_comp == d_true); % counting
acc = sum(correctMsk)/N; % rate calculation
end

结语

结果分析

运行时间

正确率

MAINPro
Accuracy is 0.975800

注：正确率会因为权重矩阵初始化的不同而有所差异。

网络优化

本例中的程序框架使用了CNN算法，其耗时283.148s（当然取决于自己的电脑了），正确率为97.58%左右。为了提高收敛速度，可以考虑使用批量算法，动量算法；为了提高正确率，可以考虑加深网络层数，使用Dropout，改变激活函数，代价函数……以改变网络性能。

写在最后
作为第一次写博客的新手、深度学习的初学者，希望大家多多包涵。
如有错误，望指正~