noip普及组模拟小赛【cpp】

---

概述

今天我们来了一场七年级与八年级的混合考，最为学长，我拿下了400分，位居第11，其实还是挺不错的，倒是也有两人AK~~不过对自己的成绩已经算满意了吧

顺序

• 1.Classroom Watch
• 2.组合技能
• 3.表面积
• 4.红皇后的旅行
• 5.构造序列

---

1.Classroom Watch

【问题描述】

给出一个正整数 n，现在问存在多少个 x，使得 x在十进制下的每一位之和加上 x 等于 n。

【输入】

共 1 行，一个正整数n 。

【输出】

第一行输出一个整数 m，表示有 m 个符合条件的 （若没有符合条件的 ，请只输出一个 0）。
下面m行，每行一个 x ，x按从小到大输出。

【输入输出样例】

input

21

output

1
15

【数据范围】

分析

因为把x拆开，各数位累加和最多不会超过9*9=81
所以我们只需要枚举N-100到N的所有数，验证一下即可

#include
using namespace std;
const int N=1e9;
int m,n,j,len;
int a[102];
int dfs(int i,int x)
{
	if(i==0)return x;
	else
	{
		x+=i%10;
		i/=10;
		return dfs(i,x);
	}
}
int main()
{
	freopen("num.in","r",stdin);
	freopen("num.out","w",stdout); 
	int i;
	scanf("%d",&n);
	for(i=max(n-10*10-1,0);++i<n;)
	{
		int x=dfs(i,0);
		if(x+i==n)a[++len]=i;
	}
	printf("%d\n",len);
	for(i=0;++i<=len;)printf("%d\n",a[i]);
	
	return 0;
}

---

2.组合技能

题目描述

蓝月商城出新技能书了！！
如果古天乐想购买“旋风斩”，则他需要花费A元；如果古天乐想买“半月弯刀”，则需要B元；如果古天乐两个一起买，则需要C元。
蓝月的设计师非常有头脑，每样商品的利润都是相同的。即假设旋风斩和半月弯刀的成本为a,b元，则A-a=B-b=C-a-b。
给出A，B，C求出利润，数据保证为正数。

格式

输入第一行一个数T，表示T次询问。
接下来T行，每行三个数A,B,C
输出T行，每行一个数，表示利润。

范围

T <= 100
A,B,C <= 2000

Sample Input 0

3
275 214 420
6 9 11
199 199 255

Sample Output 0

69
4
143

太简单不过了~
小学二年级数学~
设利润为x
A-a=B-b=C-a-b
A-a+B-b=2x,C-a-b=x
A-a+B-b-x=C-a-b
x=A+B-C

#include
using namespace std;
int A,B,C,b,t;
int main()
{
	freopen("combo.in","r",stdin);
	freopen("combo.out","w",stdout);
	int i=0;
	scanf("%d",&t);
	for(i=0;++i<=t;)
	{
		scanf("%d%d%d",&A,&B,&C);
		printf("%d\n",B-(C-A));
	}
	
	return 0;
}

---

3.表面积

题目描述

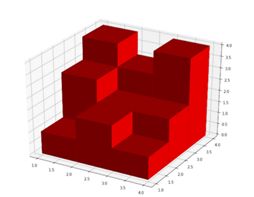
古天乐在搭积木，积木图可以抽象为一个n*m的网格图，其中第(i,j)的位置有A[i][j]个积木。求表面积。

格式

输入第一行两个数n,m，接下来n行每行m个数，表示A[i][j]。
输出一个数，表示表面积。

范围

Sample Input 0

1 1
1

Sample Output 0

6

Sample Input 1

3 3
1 3 4
2 2 3
1 2 4

Sample Output 1

60

每个面累加枚举，去掉重叠

#include
using namespace std;
int i,j,h,k,n,m,S;
int a[205][205];
inline const int read() 
{
    int num=0,bj=1;char x=getchar();
    while(x<'0'||x>'9') {if(x=='-')bj=-1;x=getchar();}
    while(x>='0'&&x<='9') {num=num*10+x-'0';x=getchar();}
    return num*bj;
}
void work()
{
	for(i=0;++i<=n;)
	  for(j=0;++j<=m;)
	  {
	  	k=a[i][j];
//	  	if(k==0)continue;
	  	S+=6*k-(k-1)*2;
	  	S-=min(a[i][j-1],k)*2;
	  	S-=min(a[i-1][j],k)*2;
	  }
}
int main()
{
	freopen("surface.in","r",stdin);
	freopen("surface.out","w",stdout);
    for(n=read(),m=read(),i=0;++i<=n;)
	  for(j=0;++j<=m;)
	    a[i][j]=read();
	work();
	printf("%d",S); 
	
	return 0;
}

---

4.红皇后的旅行

题目描述

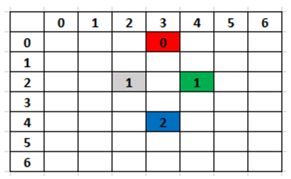
给定一个n*n的棋盘，行和列标号为0,1,2,….,n-1。在棋盘的(i_start,j_start)位置上有一位红皇后每次红皇后可以往六个方向走，如图所示：
现在红皇后想去(i_end,j_end)点，求最短距离，并且输出一条路径。
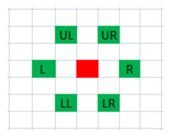
显然最短路径有无穷条，请按照以下顺序来搜索：UL, UR, R, LR, LL, L。
如果无解，输出Impossible

格式

输入第一行一个数n，第二行四个数，i_start,j_start，i_end,j_end。
输出第一行一个数，最小步数，第二行输出方案。

范围

Sample Input 0

7
6 6 0 1

Sample Output 0

4
UL UL UL L

Sample Input 1

6
5 1 0 5

Sample Output 1

Impossible

Sample Input 2

7
0 3 4 3

Sample Output 2

2
LR LL

本题直接用BFS就可以求出最小步数了

#include
using namespace std;
int n,i_start,j_start,i_end,j_end;
struct sss
{
	int x, y;
	string t;
} t[6] = { {-2,-1,"UL"}, {-2,+1,"UR"}, {0,+2,"R"}, {+2,+1,"LR"}, {+2,-1,"LL"}, {0,-2,"L"} };
int cnt;
string a[40004];
struct ss
{
	int x, y, t, last;
}q[40004];
int head, tail;
bool v[202][202];
inline bool bfs( int x1, int y1, int x2, int y2 )
{
	for (head=1,tail=0,q[++tail]={x1,y1,0,1},v[x1][y1]=true;tail>=head;head++)
	{
		for (int tx,ty,i=-1;++i<6;)
		{
			tx=q[head].x+t[i].x;ty=q[head].y+t[i].y;
			if(0<=tx&&tx<n&&0<=ty&&ty<n&&!v[tx][ty] )
			{
				q[++tail]={tx,ty,i,head};
				v[tx][ty]=1;
				if(tx==x2&&ty==y2)
				{
					for(int node=tail;node!=q[node].last;node=q[node].last)a[++cnt]=t[q[node].t].t;
					return 1;
				}
				
			}
		}
	}
	return false;
}
int main()
{
	freopen("redqueen.in","r",stdin);
	freopen("redqueen.out","w",stdout);
	scanf( "%d\n%d %d %d %d", &n, &i_start, &j_start, &i_end, &j_end );
	if ( bfs( i_start, j_start, i_end, j_end ) )
	{
		printf( "%d\n", cnt );
		for(int i=cnt;i>=1;i-- )
		printf("%s ",a[i].c_str());
	}
	else puts("Impossible");
	return 0;
}

---

5.构造序列

题目描述

有一个长度为n的序列A，其中A[1]=1,A[n]=x，A[2…n-1]可以是1至k间任意一个正整数。求有多少个不同的序列，使得相邻两个数不同。
答案对10^9+7取模。

格式

输入共一行，包含三个数，n,k,x。
输出一个数，表示答案。

范围

Sample Input 1

4 3 2

Sample Output 1

3

这题其实啊，其实呢，是很简单的
（丢脸~~）
先设F[i][j]
这个不难看出，很好列方程
$$F[i][j]=F[i-1][1]+...F[i-1][k]-F[i-1][j]$$
我们要求的是F[i][x]
所以我们可以对这个式子进行转移并化简
$$F[i-1][k]=(F[i-2][1]\cdot \cdot \cdot +F[i-2][k])\ast (k-1)$$
很明显为了时间优化，我们可以预处理上面的式子
于是f就可以优化到一维，就有了
$$dp[i]=(dp[i-1])(k-1)$$
$$f[i]=dp[i-1]-f[i-1]$$

#include
using namespace std;
const int N=1e5+5;
const int MOD=1e9+7;
long long f[N],dp[N];
long long n,m,k,x,i;
int main()
{
//	freopen("construct.in","r",stdin);
//	freopen("construct.out","w",stdout);
	scanf("%lld%lld%lld",&n,&k,&x);
   
	for(dp[i]=0,dp[2]=k-1,i=2;++i<=n;)
	  dp[i]=dp[i-1]*(k-1)%MOD;
	if(x==1)f[2]=0;else f[2]=1;
	for(i=2;++i<=n;)
	  f[i]=(dp[i-1]-f[i-1]+MOD)%MOD; 
    
    printf("%lld",f[n]);
	
	return 0;
}

---

好像很快结束了呢~~

那么再见了~~！！