算法 - 求路径和
题目
给定一个矩形的迷宫,左上角有一个机器人,右下角是目的地。这个机器人只能向下走或者是向右走,请问这个机器人走到目的地的路径一共有多少种?矩形的长和宽都不超过100.
示例
Input: m = 3, n = 2 Output: 3 Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner: 1. Right -> Right -> Down 2. Right -> Down -> Right 3. Down -> Right -> Right
分析
思路一:作为智力题有一个标准的模板式解法
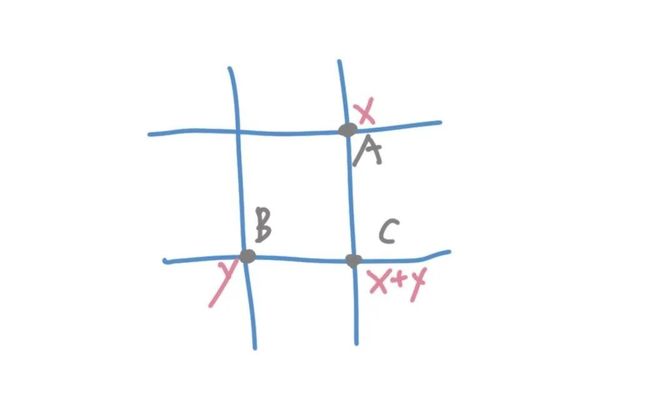
对于图中的C点来说,从起点通往它的路径数量等于通往A点和B点路径的和。
C点的上游是A点和B点,也就是说C状态是由A状态或者是B状态转移到的。这就是一个动态规划算法
我们用dp记录每一个位置的答案的话,那么可以很轻松地写出状态转移方程:
dp[i][j] = dp[i-1][j] + dp[i][j-1]解法:
class Solution {
int uniquePaths(int m, int n) {
int dp[100][100] = {0};
dp[0][1] = 1;
for (int i = 1; i < m+1; i++) {
// 特殊处理第一列,因为第一列只有1种
dp[i][1] = dp[i-1][1];
for (int j = 2; j < n+1; j++) {
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m][n];
}
};
思路二:排列组合
我们来分析一下问题,机器人要从左上角走到右下角,地图是没有缺陷的,所有点都可以到达。由于机器人没办法走回头路,也就是说机器人在通往终点的过程当中走过的路程是确定的。也就是要走n-1条横边和m-1条竖边。
边的总数和种类都确定了,其实这个问题可以转化一下。我们把走的横边看成是白球,走的竖边看成是黑球,那么这道题其实就可以转化成,我们有n-1个白球,m-1个黑球,现在把它们排成一排,一共有多少种方法?
这个是小学的组合数学问题,我们要从整体的n+m-2个物体当中,选出n-1个,那么显然答案就是:![]()
要求解这个组合数,还是需要通过循环的。我们把它转化成:
解法:
class Solution {
int uniquePaths(int m, int n) {
int ret = 1;
for(int i = 1; i < n; i++) {
ret = ret * (n + m - 1 - i) / i;
}
return ret;
}
};扩展
如果行和列中有格子无法通过,那总线路数如何求得?
Input:
[ [0,0,0],
[0,1,0],
[0,0,0]
]
Output: 2
Explanation: There is one obstacle in the middle of the 3x3 grid above. There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
思路
我们套用一下上题的思路,其中动态规划的解法是完全适用的。路障的存在只会影响路障的点本身以及它附近可以转移到的点,对于它本身而言,它无法到达,自然可访问的路径数就是0。而对于它转移到的点来说,这点无法访问,自然贡献也是0。所以我们只需要在转移的过程当中将路障的位置置为0即可。
class Solution {
int uniquePaths(int obstacleGrid[][], int m, int n) {
int dp[100][100] = {0};
dp[0][1] = 1;
for (int i = 1; i < m+1; i++) {
// 特殊处理第一列,因为第一列只有1种
dp[i][1] = dp[i-1][1];
for (int j = 2; j < n+1; j++) {
if (obstacleGrid[i-1][j-1] == 1) {
dp[i][j] = 0;
} else {
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
}
return dp[m][n];
}
};我们dp数组维护的下标范围和题目给定的路障数组的下标是不一样的,我们设置了下标从1开始,这样可以不用考虑转移时数组越界的问题。既然下标设置从1开始,我们在判断对应位置是否是路障的时候,就需要i和j都-1。
扩展
如果路径上面带权值,如何求得最短路径?
Input:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
Output: 7
Explanation: Because the path 1→3→1→1→1 minimizes the sum.
思路:对于每一个点i,j来说,它有两个来源,分别是i-1,j 和i, j-1。状态转移方程就是
dp[i][j] = min(dp[i-1][j], dp[i],[j-1])cost[i][j]这里的cost数组也就是题目给的每个点的花费。
这里我们用了一个巧妙的方法,我们令![]() ,这是为了给
,这是为了给![]() 一个消耗为0的入口。这样当我们执行
一个消耗为0的入口。这样当我们执行![]() 的时候,就会获得0,这样
的时候,就会获得0,这样![]() 就会自动完成,就不用我们在循环当中进行特判了。当然使用 if 特判也是可以的,但是这样写感觉更简洁一些。
就会自动完成,就不用我们在循环当中进行特判了。当然使用 if 特判也是可以的,但是这样写感觉更简洁一些。