二叉树遍历及C语言实现

二叉树遍历及C语言实现

已知中序和前序序列，或者已知中序和后序序列，都能够构造一棵二叉树。在本例中，本人用C语言写程序解答了下面两个算法题：

（1）给出一棵二叉树的中序与后序遍历序列，求出它的先序遍历序列。

（2）给出一棵二叉树的中序与先序遍历序列，求出它的后序遍历序列。

知识点扼要回顾：
所谓二叉树的遍历，是指按一定的顺序对二叉树中的每个结点均访问一次，且仅访问一。按照根结点访问位置的不同，通常把二叉树的遍历分为六种：
TLR（根左右）, TRL（根右左）, LTR（左根右）
RTL（右根左）, LRT（左右根）, RLT（右左根）

其中，TRL、RTL和RLT三种顺序在左右子树之间均是先右子树后左子树，这与人们先左后右的习惯不同，因此，往往不予采用。余下的三种顺序TLR、LTR和LRT根据根访问的位置不同分别被称为前序遍历、中序遍历和后序遍历。

前序遍历的规律是：输出根结点，输出左子树，输出右子树； 
中序遍历的规律是：输出左子树，输出根结点，输出右子树；
后序遍历的规律是：输出左子树，输出右子树，输出根结点；

不多说了，看代码吧：）

#include #include using namespace std; //存储节点数据，为简便起见，这里选用字符 typedef char DATA_TYPE; typedef struct tagBINARY_TREE_NODE BINARY_TREE_NODE, *LPBINARY_TREE_NODE; struct tagBINARY_TREE_NODE { DATA_TYPE data; //节点数据 LPBINARY_TREE_NODE pLeftChild; //左孩子指针 LPBINARY_TREE_NODE pRightChild; //右孩子指针 }; // //函数名称：TreeFromMidPost //函数功能：给出一棵二叉树的中序与后序序列，构造这棵二叉树。 //输入参数：LPBINARY_TREE_NODE & lpNode：二叉树的结点 // string mid：存储了二叉树的中序序列的字符串 // string post：存储了二叉树的后序序列的字符串 // int lm, int rm：二叉树的中序序列在数组mid中的左右边界 // int lp, int rp：二叉树的后序序列在数组post中的左右边界 // void TreeFromMidPost(LPBINARY_TREE_NODE & lpNode, string mid, string post, int lm, int rm, int lp, int rp) { //构造二叉树结点 lpNode = new BINARY_TREE_NODE; lpNode->data = post[rp]; lpNode->pLeftChild = NULL; lpNode->pRightChild = NULL; int pos = lm; while (mid[pos] != post[rp]) { pos++; } int iLeftChildLen = pos - lm; if (pos > lm)//有左孩子，递归构造左子树 { TreeFromMidPost(lpNode->pLeftChild, mid, post, lm, pos - 1, lp, lp + iLeftChildLen - 1); } if (pos < rm)//有右孩子，递归构造右子树 { TreeFromMidPost(lpNode->pRightChild, mid, post, pos + 1, rm, lp + iLeftChildLen, rp - 1); } } // //函数名称：TreeFromMidPre //函数功能：给出一棵二叉树的先序与中序序列，构造这棵二叉树。 //输入参数: BINARY_TREE_NODE & lpNode：二叉树的结点 // string mid：存储了二叉树的中序序列的字符串 // string pre：存储了二叉树的先序序列的字符串 // int lm, int rm：二叉树的中序序列在数组mid中的左右边界 // int lp, int rp：二叉树的先序序列在数组pre中的左右边界 // void TreeFromMidPre(LPBINARY_TREE_NODE & lpNode, string mid, string pre, int lm, int rm, int lp, int rp) { //构造二叉树结点 lpNode = new BINARY_TREE_NODE; lpNode->data = pre[lp]; lpNode->pLeftChild = NULL; lpNode->pRightChild = NULL; int pos = lm; while (mid[pos] != pre[lp]) { pos++; } int iLeftChildLen = pos - lm; if (pos > lm)//有左孩子，递归构造左子树 { TreeFromMidPre(lpNode->pLeftChild, mid, pre, lm, pos - 1, lp + 1, lp + iLeftChildLen); } if (pos < rm)//有右孩子，递归构造右子树 { TreeFromMidPre(lpNode->pRightChild, mid, pre, pos + 1, rm, lp + iLeftChildLen + 1, rp); } } //先序遍历 void PreOrder(LPBINARY_TREE_NODE p) { if(p != NULL) { cout << p->data; //输出该结点 PreOrder(p->pLeftChild); //遍历左子树 PreOrder(p->pRightChild); //遍历右子树 } } //中序遍历 void MidOrder(LPBINARY_TREE_NODE p) { if(p != NULL) { MidOrder(p->pLeftChild); //遍历左子树 cout << p->data; //输出该结点 MidOrder(p->pRightChild); //遍历右子树 } } //后序遍历 void PostOrder(LPBINARY_TREE_NODE p) { if(p != NULL) { PostOrder(p->pLeftChild); //遍历左子树 PostOrder(p->pRightChild); //遍历右子树 cout << p->data; //输出该结点 } } //释放二叉树 void Release(LPBINARY_TREE_NODE lpNode) { if(lpNode != NULL) { Release(lpNode->pLeftChild); Release(lpNode->pRightChild); delete lpNode; lpNode = NULL; } } int main(int argc, char* argv[]) { string pre; //存储先序序列 string mid; //存储中序序列 string post; //存储后序序列 LPBINARY_TREE_NODE lpRoot; //二叉树根节点指针 cout<<"程序１已知二叉树的中序与后序序列，求先序序列"<> mid; cin >> post; TreeFromMidPost(lpRoot, mid, post, 0, mid.size()-1, 0, post.size()-1); cout<<"先序遍历结果："; PreOrder(lpRoot); cout<> pre; cin >> mid; TreeFromMidPre(lpRoot, mid, pre, 0, mid.size()-1, 0, pre.size()-1); cout<<"先序遍历结果："; PreOrder(lpRoot); cout<

（1）程序1的输入方式：
已知二叉树的中序与后序序列，求先序序列，请先输入中序序列，回车后输入后序序列：
例如输入：
DGBAECHF
GDBEHFCA
输出：
先序遍历结果：ABDGCEFH
中序遍历结果：DGBAECHF
后序遍历结果：GDBEHFCA

（2）程序2的输入方式：
已知二叉树的先序与中序序列，求后序序列，请先输入先序序列，回车后输入中序序列：
例如输入：
abdefgc
debgfac
输出：
先序遍历结果：abdefgc
中序遍历结果：debgfac
后序遍历结果：edgfbca

最后请看该程序运行效果图：

这是程序1所确定的二叉树图：

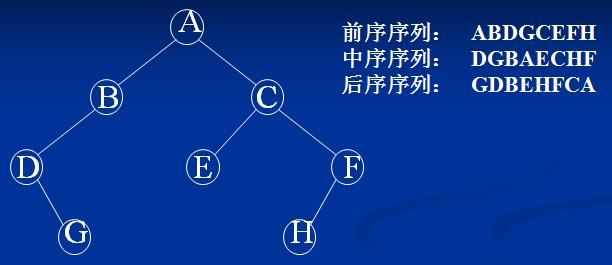
这是程序2所确定的二叉树图：

by Loomman, QQ:28077188, MSN: [email protected] QQ裙：30515563 ☆程序天堂☆ 请尊重作者原创，转载注明来自裂帛一剑博客，谢谢合作。