四阶龙格库塔方程解二阶常微分方程组并计算船舶在迎浪下的纵摇埀荡耦合运动方程-附Python代码

0 写在前面

这篇博客是在将我上一篇博客的matlab代码移植到python中，应为后续要开展深度强化学习下的船舶减摇研究，总的来说还是在python上做这项工作比较合适。具体方程的解法和背景不在赘述，见https://blog.csdn.net/Mezikov/article/details/107461970

1 代码

import math
import numpy as np
import matplotlib.pyplot as plt
from math import e
from numpy import reshape

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

##################   写在前面：这个代码只适合用于已知浪向角的规则波   ########################

ts, ys, zs, ys_, zs_ = [], [], [], [], []
# all below is coefficients of wave
fi = math.pi / 3
B = 1
d = 0.341
delta = 1.76 * 10 ** 3
V = 1.76
g = 9.8
L = 6
lamda = 1.64
rho = 1.025 * 10 ** 3
A_w = 5.448
A_m = 0.346
C_w = A_w / (L * B)
C_p = V / (L * A_m)
C_b = delta / (1000 * L * B * d)
v = 4.44
T = 0.8 * math.sqrt(lamda)
W_0 = 2 * math.pi / T
W_e = W_0 * (1 + v * W_0 * np.cos(fi) / g)
x_b = -0.23
GM_l = (L ** 2 * (5.55 * C_w + 1) ** 3 / 3450) / (C_b * d)
M = 1.6 * 10 ** 3
H_0 = B / (2 * d)
a_zz = 0.8 * H_0 * C_w * M
b_zz = (5.4 * (C_w / C_p) * (H_0 ** 0.5) - 4.7) * delta / ((g * L) ** 0.5)
c_zz = rho * g * A_w
a_z0 = (v / W_e ** 2) * b_zz - a_zz * x_b
b_z0 = -b_zz * x_b + v * a_zz
c_z0 = -rho * g * A_w * x_b
I_00 = 0.07 * C_w * M * L ** 2
a_00 = 0.83 * H_0 * C_p ** 2 * (0.25 * L) ** 2 * (delta / g) ** 0.5
b_00 = 0.08 * H_0 * delta * L ** 2 / (g * L) ** 0.5
c_00 = rho * g * (V * GM_l)
a_0z = -(a_zz * x_b)
b_0z = -(b_zz * x_b)
c_0z = -rho * g * A_w * x_b - v * b_zz
fi = math.pi / 3
a = 0.5 * 0.17 * lamda ** (3 / 4)
k = 2 * math.pi / lamda
n1 = (I_00 + a_00) - (a_0z * a_z0) / (M + a_zz)
n2 = rho * g * a * k * math.e ** (-k * d / 2) * B * d * np.sin(k * B * L * np.sin(fi) / 2) / (
            k * B * L * np.sin(fi) / 2)
n3 = (I_00 + a_00) * (M + a_zz) - a_0z * a_z0


#################   以上全是水动力系数的计算,下面是四阶龙格库塔算法   ######################
def cal_F(t):
    m1 = 547 * np.cos(5.53 * t)
    m2 = 1045 * np.sin(5.53 * t)
    F_ = (I_00 + a_00) / n3 * m1 - a_z0 / n3 * m2
    return F_


def g(y1, z1, y2, z2):
    j = (b_zz * (I_00 + a_00) - a_z0 * b_0z) / n3 * z1 + \
        (c_zz * (I_00 + a_00) - a_z0 * c_0z) / n3 * y1 + \
        (b_z0 * (I_00 + a_00) - a_z0 * b_00) / n3 * z2 + \
        (c_z0 * (I_00 + a_00) - a_z0 * c_00) / n3 * y2
    # 文献结果
    # j= 0.9716*np.cos(1.245*t-0.5566)-0.0674*np.cos(1.245*t-1.4375)-0.5252*z1-1.1424*y1-2.1741*z2-3.5594*y2
    return j


def cal_M(t):
    m1 = 547 * np.cos(5.53 * t)
    m2 = 1045 * np.sin(5.53 * t)
    M_ = (M + a_zz) / n3 * m1 - a_0z / n3 * m2
    return M_


def g_(y1, z1, y2, z2):
    # m1 = 547*np.cos(5.53*t)
    # m2 = 1045*np.sin(5.53*t)
    # j = (0.2580 * np.sin(5.53 * t) - 0.0042 * np.cos(5.53 * t)) - 0.2137 * z2 - 33.3415 * y2 - 0.0036 * z1 - 0.1641 * y1
    j = (b_00 * (M + a_zz) - a_0z * b_z0) / n3 * z2 + \
        (c_00 * (M + a_zz) - a_0z * c_z0) / n3 * y2 + \
        (b_0z * (M + a_zz) - a_0z * b_zz) / n3 * z1 + \
        (c_0z * (M + a_zz) - a_0z * c_zz) / n3 * y1
    # j=1.1854*np.cos(1.245*t- 1.4375)-0.006*np.cos(1.245*t-0.5566)-7.9154*z2-20.3425*y2-0.0305*z1-0.0547*y1
    return j

def runge_kutta():
    """
        兄弟们，之前这里被网上的资料坑了，我发现按照oringin_try里面的办法，龙格库塔里面只有return的那个量会
        更改，其余变量都不变化，如果这是个一阶微分方程，那只有一个量在变化，可现在是二元二阶方程组啊！我现在改
        过来了，就用这种新方法了。
    """
    t = 0
    dt = 0.1
    y1 = 0
    z1 = 0
    y2 = 0
    z2 = 0
    while t <= 500:
        ys.append(y1)
        zs.append(z1)
        ys_.append(y2)
        zs_.append(z2)
        ts.append(t)
        t += dt

        k1 = z1  # f(t,y1,z1,y2,z2)
        k1_ = z2  # f_(t,y1,z1,y2,z2)
        l1 = cal_F(t) - g(y1, z1, y2, z2)
        l1_ = cal_M(t) - g_(y1, z1, y2, z2)
        k2 = z1 + 0.5 * dt * l1
        k2_ = z2 + 0.5 * dt * l1_
        l2 = (cal_F(t) + cal_F(t + dt)) / 2 - g(y1 + 0.5 * dt * k1, z1 + 0.5 * dt * l1, y2 + 0.5 * dt * k1_,
                                                z2 + 0.5 * dt * l1_)
        l2_ = (cal_M(t) + cal_M(t + dt)) / 2 - g_(y1 + 0.5 * dt * k1, z1 + 0.5 * dt * l1, y2 + 0.5 * dt * k1_,
                                                  z2 + 0.5 * dt * l1_)
        k3 = z1 + 0.5 * dt * l2
        k3_ = z2 + 0.5 * dt * l2_  #  我曹之前这里z2+0.5+dt*l2，我说怎么会这么奇怪一直和Matlab对不上,写代码不能分心！
        l3 = (cal_F(t) + cal_F(t + dt)) / 2 - g(y1 + 0.5 * dt * k2, z1 + 0.5 * dt * l2, y2 + 0.5 * dt * k2_,
                                                z2 + 0.5 * dt * l2_)
        l3_ = (cal_M(t) + cal_M(t + dt)) / 2 - g_(y1 + 0.5 * dt * k2, z1 + 0.5 * dt * l2, y2 + 0.5 * dt * k2_,
                                                  z2 + 0.5 * dt * l2_)
        k4 = z1 + dt * l3  # wo ta ma zhengde cao le 这里我为什么z1会乘以0.5啊。
        k4_ = z2 + dt * l3_  # f_(t,y1,z1,y2,z2)+0.5*dt*l3_
        l4 = cal_F(t + dt)- g(y1 + dt * k3, z1 + dt * l3, y2 + dt * k3_,
                                                z2 + dt * l3_)  # 又乘了0.5，第四步应该都是dt而不是0.5*dt
        l4_ = cal_M(t + dt)- g_(y1 + dt * k3, z1 + dt * l3, y2 + dt * k3_, z2 + dt * l3_)

        y1 = y1 + dt * (k1 + 2 * k2 + 2 * k3 + k4) / 6
        z1 = z1 + dt * (l1 + 2 * l2 + 2 * l3 + l4) / 6
        y2 = y2 + dt * (k1_ + 2 * k2_ + 2 * k3_ + k4_) / 6
        z2 = z2 + dt * (l1_ + 2 * l2_ + 2 * l3_ + l4_) / 6


###################   主程序入口，代码到这里就算编完了  #########################3
if __name__ == "__main__":
    runge_kutta()
    print(ys)
    # print(ys)
    plt.figure(1)
    plt.plot(ts[2000:3000], zs[2000:3000], label='埀荡')
    plt.xlabel('time(s)')
    plt.ylabel('埀荡量(m)')
    plt.legend()
    plt.show()
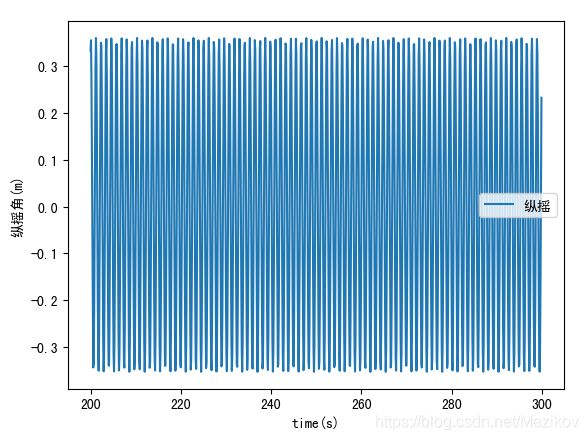
    plt.figure(2)
    plt.plot(ts[2000:3000], zs_[2000:3000], label='纵摇')
    plt.xlabel('time(s)')
    plt.ylabel('纵摇角(m)')
    plt.legend()
    plt.show()
    print('最大埀荡量', np.max(ys), )
    print('最大纵摇角', np.max(ys_), )

2 结果

3 总结

但是不知道为什么，matlab算的和python算的结果有一点点（2%左右误差）不一样，这是为什么呢